nextupprevious

Next:4.10 Методы порождения объектов
Up:4 Разработка алгоритмов
Previous:4.8 Метод ветвей и границ

4.9 Динамическое программирование

Пусть имеется представление исходной задачи в виде иерархии вложенных подзадач разного размера таким образом, что есть прямые алгоритмы решения элементарных (не содержащих других) подзадач и есть простое сведение любой неэлементарной подзадачи (в том числе и самой задачи) к подзадачам меньшего размера.

В этом случае для решения задачи можно использовать очевидный рекурсивный алгоритм. Однако, не всегда рекурсивная техника дает удовлетворительное решение. Например, если разбиение таково, что решение размера $n$ сводится к $n$ подзадачам размера $n-1$, то рекурсивный алгоритм будет, по-видимому, не приемлемым из-за его экспоненциальной сложности. Другой пример, это возможная неэффективность рекурсивного алгоритма, возникающая из-за большого числа повторений решения одной и той же подзадачи, как это имеет место, например, при вычислении $n$-ого числа Фибоначчи по формуле $Fib(n)=Fib(n-1)+Fib(n-2)$.

Часто в этом случае можно получать эффективные алгоритмы с помощью табличной техники, называемой динамическим программированием. Динамическое программирование предполагает последовательное решение всех подзадач исходной задачи в порядке возрастания их размера с запоминанием ответов в специальной таблице по мере их получения. Преимущество этого метода по сравнению с рекурсивным алгоритмом состоит в том, что раз уж подзадача решена, ее ответ размещен в таблицу и в дальнейшем никогда не вычисляется повторно. Ответ подзадачи берется из таблицы каждый раз, когда он нужен для нахождения решения подзадачи большего размера. Понятно, что эта техника позволяет получать эффективные алгоритмы в тех случаях, когда объем хранимой в таблице информации оказывается не слишком большим.

Рассмотрим применение техники динамического программирования еще на одном простом примере. Рассматривается множество так называемых раскроев выпуклого $n$-угольника или, что то же самое, различных разбиений его на треугольники с помощью $n-3$ непересекающихся диагоналей. Стоимость конкретного раскроя -- это суммарная длина проведенных диагоналей. Пусть дан выпуклый $n$-угольник. Требуется найти его раскрой минимальной стоимости.

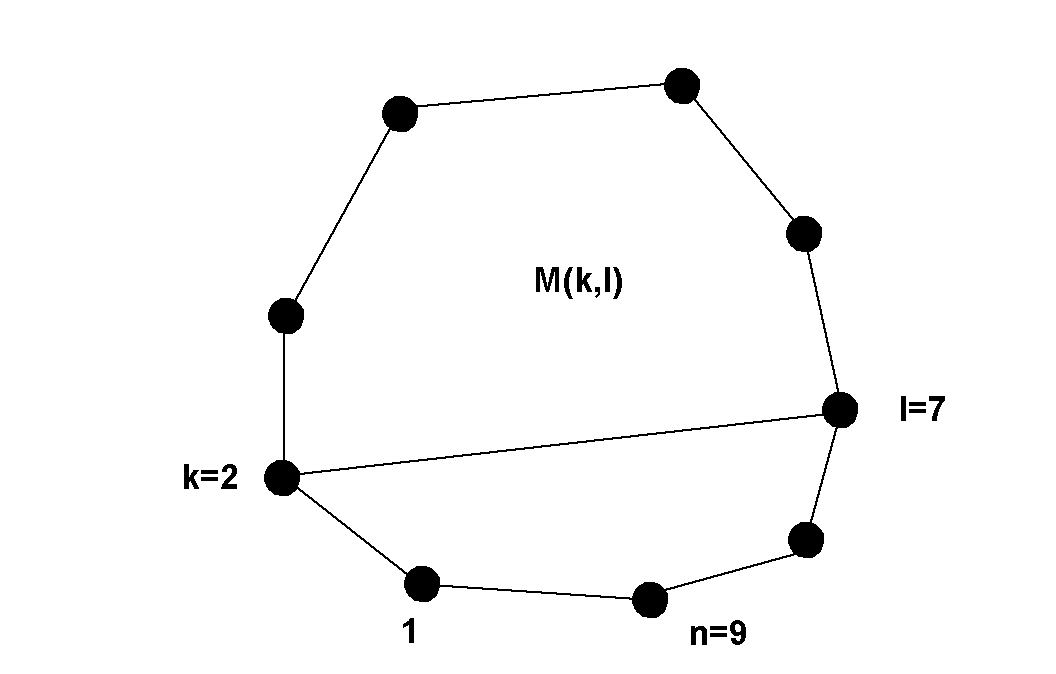
Рис. 24.

Будем считать, что все вершины исходного многоугольника пронумерованы в порядке обхода $n$-угольника по часовой стрелки, т.е. $n$-угольник образован отрезками $(1,2), (2,3),$$\ldots$, $(n-1,n),$$(n,1).$ Через $M(k,l)$ обозначим многоугольник, отрезаемый от исходного диагональю $(k,l),$ где $k\leq l.$ Он образован отрезками $(k,l)$, $(k+1,k+2)$, $\ldots$, $(l-1,l)$ (см. рис. 24). Ясно, что при $l=k+1$ многоугольник $M(k,l)$ вырождается в отрезок, при $l=k+2$ он -- треугольник, а $M(1,n)$ -- это исходный $n$-угольник.

Для любых вершин $k$ и $l$ через $с(k,l)$ обозначим минимальную стоимость раскроя многоугольника $M(k,l)$, если $l>k+2$, и полагаем $с(k,l)=0$, если $l=k+1$ или $l=k+2$. Получаем следующее очевидное рекуррентное соотношение (см. рис. 24):

$с(k,l)= \min \{с(k,i)+с(i,l)+ d(k,i)+ d(i,l) : k < i < l \}$,

где $d(s,r)$ -- это длина диагонали $(s,r)$, если $r > s+1$, и $d(s,r)=0$, если $r = s+1$.

Указанное соотношение позволяет составить таблицу для $с(k,l)$, заполняя ее в порядке возрастания числа $(l-k+1)$ -- количества вершин в многоугольнике $M(k,l)$. Программа такого заполнения таблицы будет использовать память $O(n^2)$ и требовать время $O(n^3)$, поскольку всего существует $O(n^2)$ элементов таблицы, а для однократного применения рекуррентной формулы требуется осуществить выбор минимального числа из не более чем $n$ чисел.

После того, как вычислена таблица значений $с(k,l)$, мы получаем минимальную стоимость раскроя (она равна $с(1,n)$) и легко можем вычислить раскрой минимальной стоимости. Для этого можно реализовать процесс обработки подзадач в порядке убывания их размера. Процесс начинается обработкой исходной задачи и постепенно шаг за шагом находит диагонали, образующие разрез минимальной стоимости. На каждом шаге рассматривается многоугольник $M(k,l)$ и ищется такая вершина $i$, $k<i<l$, что
$с(k,l)= с(k,i)+с(i,l)+ d(k,i)+ d(i,l)$.

Поскольку таких шагов будет меньше $n$, а на каждом шаге требуется осуществить сравнение числа $с(k,l)$ со значениями не более чем $n$ сумм

$с(k,i)+с(i,l)+ d(k,i)+ d(i,l)$,

получаем оценку $O(n^3)$ для суммарной временной сложности двух этапов рассмотренного алгоритма.

Next:4.10 Методы порождения объектов
Up:4 Разработка алгоритмов
Previous:4.8 Метод ветвей и границ

© В.Н. Касьянов, Е.В.Касьянова,2004