6.1.6 Использование процедур и функций для пошаговой разработки программ

Механизм подпрограмм является хорошим инструментом для поддержки пошаговой разработки программы "сверху вниз", начиная с ее внешней спецификации (см. п. 4.1.5). Эту разработку можно рассматривать как нисходящее программирование, при котором сначала задача решается в терминах операций (вызовов запрограммированных операций) виртуальной машины, наиболее подходящей для решения данной задачи, а затем, посредством последовательных декомпозиций, связанных с программированием этих операций в терминах менее абстрактных виртуальных машин, постепенно осуществляется спуск к виртуальной машине, реализованной в языке Zonnon (т.е. к ВМ). Например, использование подпрограмм в ходе нисходящего проектирования программы ДлинаМаксимумМинимум, рассмотренного в п. 4.1.5, приводит к следующему результату:

program ДлинаМаксимумМинимум;
    procedure Обработка;
        { Читает заданную непустую последовательность целых чисел и
        печатает длину последовательности,наибольшее и наименьшее числа в ней }
        var K : integer; (*Для хранения |Input| *)
                M : Integer; (* Для хранения Максимум(Input1) *)
                N : Integer; (* Для хранения Минимум(Input1) *)
        procedure ЧитатьПервый;
                (*Вводит первый непрочитанный элемент A и устанавливает M=A, N=A и K = 1*)
        begin read(M); N := M; K := 1 end ЧитатьПервый;
        procedure ЧитатьХвост;
               { Если не пуста последовательность $\beta=Input2$, то она вводится и вычисляются
                в переменных M, N, K значения $\max(M, Макс(\beta)),\min(N, Мин(\beta)),K +\mid \beta\mid$ }
              procedure ЧитатьТекущий;
                    {Вводит B=Голова(Input2)
                    и устанавливает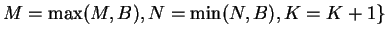$M =\max(M,B), N = \min(N,B), K = K + 1\}$
                    var X : Integer; {Для хранения Последний(Input1) }
                    procedure МиниМакс;
                          (*$\{M := \max(M,X), N := \min(N,X)\}$*)
                    begin if X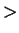$>$M then M:=X else if X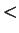$<$N then N:=X end МиниМакс;
              begin Read(X); МиниМакс; K := K + 1 end ЧитатьТекущий;
        begin whilenot Eof do ЧитатьТекущий end ЧитатьХвост;
        procedure Печать; begin Write(K,M,N) end;
    begin ЧитатьПервый; ЧитатьХвост; Печать end;
begin Обработка end.

Первый уровень описания решения нашей задачи, представленной внешней спецификацией "Длина, максимум и минимум последовательности целых чисел" (см. п. 4.1.5), -- это выполнение одной операции Обработка наиболее подходящей (абстрактной) виртуальной машины. На следующих шагах разработки уточняются те операции, использованные в программе, которые не являются операциями ВМ, путем их программирования в терминах элементарных операций виртуальной машины все более низкого уровня абстракции. Постепенно таким образом происходит спуск к конечному уровню, уровню языка Паскаль, реализованного в машинных операциях ВМ.

Видно, что механизм подпрограмм хорошо поддерживает принцип декомпозиции задачи на уровни абстракции. При этом он допускает не только нисходящее, но и восходящее программирование, когда, начиная с ВМ и поднимаясь к решаемой задаче (ее внешней спецификации), программист последовательно переходит ко все более и более высокому уровню абстракции, создавая виртуальные машины со все более "крупными" операциями.

Несомненно, что нисходящий метод программирования очень естествен: нет более логичного подхода к решению задачи, чем метод ее многократного разбиения на более простые подзадачи до тех пор, пока не будет достигнут уровень, на котором решение получается непосредственно (в языковых терминах). Вместе с тем имеется ряд сложностей, связанных с применением метода нисходящего программирования. Укажем на две основные из них. Первая сложность состоит в том, что решения по выбору структур данных и действий на более высоких уровнях становятся определяющими; если некоторый выбор на высоком уровне сделан преждевременно, то часто оказывается трудно к нему возвратиться, не переписав заново всю программу. Поэтому метод нисходящего программирования требует чрезвычайно строгого и внимательного выполнения основного принципа: на каждом шаге решать все те и только те вопросы, без решения которых нельзя обойтись на этом шаге, а решение всех остальных вопросов откладывать на более поздние шаги разработки. Другая сложность связана с тем, что, делая независимые уточнения, программист вынужден будет в разных частях программы похожие процессы вычисления записывать каждый раз заново. Поэтому иногда оказывается полезным восходящее программирование (всей программы или некоторых ее частей), позволяющее обнаружить части программы, поддающиеся обобщению ("запроцедуриванию").

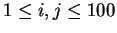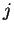Рассмотрим небольшой пример. Пусть на входе имеется двести вещественных чисел $a_1,\ldots,a_{100}, b_1,\ldots,b_{100}$. Требуется построить две матрицы $A = \{A_{ij}\}$ и $B = \{B_{ij}\}$, где $1 \leq i, j \leq 100$, $A_{ij} = a_j^{100-i+1}$ и $B_{ij} =b_j^{100-i+1}$ для всех $i$ и $j$, и напечатать ту из них, в которой больше сумма элементов. Задача построения подобной матрицы нам знакома (см. программу ПостроениеМатрицы в п. 5.2.3), и мы, выделяя подходящие подпрограммы, легко приходим к следующему решению:

module ПечатьМатрицы;
    const N = 100;
    type ИНДЕКС = integer; МАТРИЦА = array N, N of real;
    var A,B: МАТРИЦА;
    procedure ВВОД(var Z : МАТРИЦА);
        var K : ИНДЕКС;
    begin for K := 1 to N do Read(Z[N][K]) end end ВВОД;
    procedure ЗАПОЛНЕНИЕ(var Z : МАТРИЦА);
        var L,K : ИНДЕКС;
    begin
        for L := N-1 downto 1 do
            for K := 1 to N do Z[L, K] := Z[L+1,K] 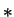$*$ Z[N,K] end
        end
    end ЗАПОЛНЕНИЕ;
    procedure Сумма(Z : МАТРИЦА) : Real;
        var L,K : ИНДЕКС; ОТВЕТ : Real;
    begin ОТВЕТ := 0;
        for L := 1 to N do
            for K := 1 to N do ОТВЕТ := ОТВЕТ + Z[L][K]
        end;
        return ОТВЕТ
    end Сумма;
    procedure ПЕЧАТЬ(Z : МАТРИЦА);
        var L,K : ИНДЕКС;
    begin
        for L := 1 to N do
            for K := 1 to N do write(Z[L][K]) end;
            writeln
        end
    end ПЕЧАТЬ;
    procedure ПОСТРОЕНИЕ(var Z : МАТРИЦА);
    begin ВВОД(Z); ЗАПОЛНЕНИЕ(Z) end;
begin
    ПОСТРОЕНИЕ(А); ПОСТРОЕНИЕ(В)
    if Сумма(A)> Сумма(B) then ПЕЧАТЬ(A) else ПЕЧАТЬ(B)end
end ДлинаМаксимумМинимум.

Из текста программы видно, что после программирования операций ВВОД, ЗАПОЛНЕНИЕ, Сумма и ПЕЧАТЬ выяснилась полезность операции ПОСТРОЕНИЕ, которая затем и была введена. Ясно, что более хорошим решением было бы вместо процедур ВВОД, ЗАПОЛНЕНИЕ и ПОСТРОЕНИЕ использовать в программе одну процедуру:

procedure ПОСТРОЕНИЕ (var Z : МАТРИЦА);
    var L,K : ИНДЕКС;
begin
     for K : =1 to N do
           read(Z[N][K]);
           for L := N-1 to 1 by -1 do Z[L,K] := Z[L+1,K] 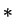$\ast$ [N,K]end
      end
end ПОСТРОЕНИЕ;

Этот пример показывает, что и при восходящем программировании выбор укрупненных операций и их программирование нужно проводить с определенными априорными предположениями об общей структуре решения задачи, что восходящее программирование, хотя иногда и удобно, является лишь дополнением к нисходящему программированию.

Как уже говорилось в п. 4.1.5, в процессе пошаговой разработки программы проводится и доказательство ее правильности. Не следует ожидать, что кто-нибудь возьмет чужую (или свою) большую программу и начнет доказывать ее правильность. Интеллектуальные затраты на такую работу были бы, вероятно, очень велики. Более того, шаги доказательства правильности программы являются существенной частью процесса ее пошаговой разработки. Программист, создавая программу по принципу "сверху вниз", составляет большой фрагмент программы, оставляя незапрограммированными некоторые его части. Доказывая правильность этого фрагмента, он исходит из того, что их выполнение будет приводит к справедливости некоторых постусловий, если до их выполнения были справедливы определенные предусловия. После этого, опираясь на эти утверждения, доказывается правильность указанного большого фрагмента. Позже, при программировании составляющих фрагмент частей, для доказательства их правильности (по отношению ко всей программе!) нужно лишь показать, что они удовлетворяют спецификации, представленной соответствующими предусловиями и постусловиями.

Механизм подпрограмм поддерживает как нисходящую, так и восходящую стратегию пошаговой разработки программ. При "восходящем" шаге, доказывая правильность получаемого фрагмента программы, можно трактовать те его части, правильность которых уже доказана, как отдельные операторы, для которых правила вывода свойств уже известны. Таким образом, при "восходящем" шаге, доказывая правильность фрагмента программы вовсе нет необходимости детально разбираться во всех его частях.
 

© В.Н. Касьянов, Е.В.Касьянова, 2004