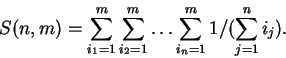
Next:6.2.4
Быстрая сортировка
Up:6.2
Построение программ с процедурами и функциями
Previous:6.2.2
Ханойские башни
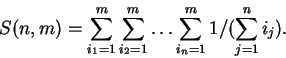
Решение. Введем в рассмотрение функцию
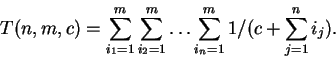
Тогда ![]() и
и
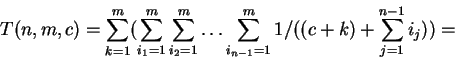
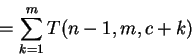
при ![]() .
При
.
При ![]() имеем
имеем ![]() .
.
Рекурсивное определение функции T можно записать на языке Zonnon.
module КратныеСуммы;
var M,N : integer;
procedure T (N,M,C : integer): real;
var I
: integer; Сумма : real;
begin Сумма := ![]() ;
;
if N
> 0 then
for I := 1 to M do Сумма := Сумма + T(N-1,M,C+I) end;
T := Сумма (* {Сумма = Т(N,M,C)} *)
else
T := 1/C (* {= T(0,M,C)} *)
end T;
begin
read(N,M); writeln('S(',N,',',M,')=',T(N,M,0))
end КратныеСуммы.
Для доказательства окончания этой программы заметим, что всякий вызов функции Т с положительным первым параметром приводит к M вызовам с меньшим на 1 значением первого параметра. Это значит, что в конце концов мы придем к вызовам функции Т с нулевым значением первого параметра, которые уже не порождают никаких вызовов.
Next:6.2.4
Быстрая сортировка
Up:6.2
Построение программ с процедурами и функциями
Previous:6.2.2
Ханойские башни