

Next:5.5
Задания
Up:5.4
Программы обработки матриц
Previous:5.4.4
Поиск номера строки-серии
5.4.5 Упражнения
1. Задана целочисленная матрица размера 20 х 20. Найти значение и координаты
(номера строки и столбца)
(1) максимального,
(2) минимального
среди всех ненулевых элементов матрицы, лежащих на главной диагонале.
Если матрица является диагональной (вне главной диагонали вся состоит из
нулей), напечатать сообщение об этом.
2. Дана целочисленная матрица размером 30 х 30. Требуется найти
(1) номер какой-нибудь из строк, содержащих наибольшее число ненулевых
элементов;
(2) номер какого-нибудь из столбцов, содержащих наименьшее число нулевых
элементов в строках с четными номерами;
(3) номер какой-нибудь из строк с минимумом среднего арифметического
положительных элементов;
(4) номер какого-нибудь из столбцов, в которых максимальное число попарно
различных элементов;
(5) номер какой-нибудь из строк, для которых скалярный квадрат (т.е.
скалярное произведение строки как вектора саму на себя) минимален;
(6) номера всех строк, представляющих собой перестановку чисел от 1
до 30;
(7) номера всех нулевых столбцов;
(8) номера всех строк, элементы которых -- степени двойки;
(9) номера всех столбцов, представляющих собой упорядоченные (по неубыванию
или невозрастанию) векторы;
(10) номера всех симметричных строк;
(11) номера всех столбцов, составленных только из четных элементов;
(12) номера всех строк, составленных только из нечетных элементов;
(13) наименьший номер строки, в которой заданное число положительных
элементов;
(14) наибольший номер столбца, элементы которого упорядочены по возрастанию;
(15) номера всех строк, совпадающих с первой;
(16) количество столбцов, совпадающих с первым;
(17) количество всех строк, содержащих не более двух разных чисел.
Если окажется, что в матрице нет ни одной строки (столбца) с требуемым
свойством, то напечатать сообщение об этом.
3. Для заданной матрицы вещественных чисел A размером 30 х 30
найти
(1) среднее арифметическое элементов, расположенных ниже главной диагонали;
(2) сумму элементов всех строк с четными номерами;
(3) произведение элементов всех столбцов, номера которых -- простые
числа;
(4) разность между средними арифметическими значений всех элементов,
расположенных ниже и выше побочной диагонали;

4. Для заданной целочисленной матрицы A размером 20 х 20 построить
вектор B длины 20 такой, что
(1) 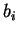 есть сумма элементов главной и побочной диагоналей, находящихся ниже
есть сумма элементов главной и побочной диагоналей, находящихся ниже 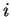 -й
строки;
-й
строки;

5. Расстояние между 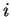 -м
и j-м (i#j) столбцами матрицы A определим как мощность множества
-м
и j-м (i#j) столбцами матрицы A определим как мощность множества 
Для данной целочисленной матрицы размера 20 х 30 найти какую-нибудь
пару
(1) максимально
(2) минимально
удаленных друг от друга столбцов и напечатать их номера.
6. Транспонировать заданную литерную матрицу A размера 30 х 30,
т.е. построить матрицу 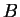 того же размера, такую что
того же размера, такую что 

В решении можно использовать только одну матрицу.
7. По заданной матрице литер размера 20 х 30 построить матрицу, которая
получается из исходной перестановкой столбцов -- первого с последним, второго
с предпоследним и т.д. В решении можно использовать только одну матрицу.
8. Построить по заданному вещественному x матрицу B следующего
вида:

9. Задана матрица A вещественных чисел размера 20 х 30. Построить
логический вектор B длины 20, в котором элемент 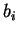 равен True тогда и только тогда, когда в матрице A
равен True тогда и только тогда, когда в матрице A
(1) все элементы 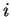 -й
строки превосходят заданное число x;
-й
строки превосходят заданное число x;
(2) все элементы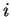 -й
строки одинаковы;
-й
строки одинаковы;
(3) 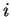 -я
строка -- упорядоченный по убыванию вектор;
-я
строка -- упорядоченный по убыванию вектор;
(4) 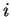 -я
строка содержит только нули;
-я
строка содержит только нули;
(5) 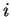 -я
строка содержит только степени двойки;
-я
строка содержит только степени двойки;
(6) 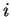 -я
строка -- симметричный вектор.
-я
строка -- симметричный вектор.
10. Упорядочить каждую строку вещественной матрицы, располагая ее элементы
(1) по неубыванию,
(2) по невозрастанию.
11. Соседями элемента матрицы  назовем
все ее элементы, у которых номера строки и столбца отличаются от
назовем
все ее элементы, у которых номера строки и столбца отличаются от 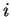 (соответственно от j) не более чем на единицу. Однако сам элемент
не считается своим собственным соседом. По заданной целочисленной матрице
A
размера 20х30 построить логическую матрицу B того же размера, в
которой элемент принимает значение
(соответственно от j) не более чем на единицу. Однако сам элемент
не считается своим собственным соседом. По заданной целочисленной матрице
A
размера 20х30 построить логическую матрицу B того же размера, в
которой элемент принимает значение  тогда и только тогда, когда
тогда и только тогда, когда
(1) все соседи элемента  строго меньше него;
строго меньше него;
(2) все соседи элемента  и
он сам равны нулю;
и
он сам равны нулю;
(3) среди соседей элемента  есть
хотя бы один нулевой;
есть
хотя бы один нулевой;
(4) среди соседей  имеется хотя бы два совпадающих с 306#192;
имеется хотя бы два совпадающих с 306#192;
(5) среди соседей элемента  имеется
ровно один четный элемент;
имеется
ровно один четный элемент;
(6) среди соседей элемента  нет
ненулевых и есть такие, знаки которых различны;
нет
ненулевых и есть такие, знаки которых различны;
(7) среди соседей элемента  есть
ровно три совпадающих.
есть
ровно три совпадающих.
12. Операция сглаживания матрицы A дает матрицу B, элемент  в которой получается как среднее арифметическое всех его соседей (см. условие
предыдущего упражнения). Построить сглаживание заданной матрицы вещественных
чисел размером 20 х 30.
в которой получается как среднее арифметическое всех его соседей (см. условие
предыдущего упражнения). Построить сглаживание заданной матрицы вещественных
чисел размером 20 х 30.
13. Назовем матрицу гладкой, если она совпадает с результатом ее сглаживания
(см. предыдущее упражнение). Определить, является ли гладкой заданная вещественная
матрица размером 20 х 30.
14. Элемент матрицы называется локальным минимумом, если он строго
меньше всех имеющихся у него соседей (см. задачу 11). Подсчитать количество
локальных минимумов заданной матрицы размером 23 x 30.
15. В условиях предыдущей задачи найти максимум среди всех локальных
минимумов заданной матрицы размеров 10 x 12.
16. Определить, становится ли симметричной (относительно главной диагонали)
заданная матрица размером 10 x 10 после замены на число 0 каждого локального
минимума (см. задачу 14).
17. Говорят, что матрица A имеет седловую точку (i, j),
если ее элемент является минимальным в
является минимальным в 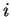 -й
строке и максимальным в j-м столбце. Найти для заданной вещественной матрицы
размером 20 х 30
-й
строке и максимальным в j-м столбце. Найти для заданной вещественной матрицы
размером 20 х 30
(1) номер строки и столбца какой-нибудь седловой точки;
(2) номера всех столбцов, в которых есть седловые точки;
(3) такую седловую точку, у которой сумма номеров строки и столбца
превышает заданное целое число.
Если соответствующих седловых точек нет, то напечатать сообщение об
этом.
18. Найти номер строки заданной литерной матрицы размером 20x30, в которой
находится самая длинная серия (серия -- это последовательность элементов,
составленная из одинаковых значений).
19. По заданной вещественной матрице A размером 20 х 20 построить
вектор
B длины 39, элементы которого -- максимумы элементов диагоналей
матрицы A, параллельных главной диагонали. При этом максимум элементов
диагонали, проходящей через элемент с индексами i, j, должен стать значением
элемента вектора 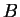 с индексом i-j+20.
с индексом i-j+20.
20. Назовем G строки вещественной матрицы G-свертку этой
строки (см. п. 5.4.4). Переставляя строки заданной матрицы размером 20х30,
расположить их в соответствии с ростом G-характеристик, где

21. Подсчитать, сколько раз встречается в заданной целочисленной матрице
размером 10 х 10 ее максимальное значение.
22. Таблица шахматного турнира задана квадратной целочисленной матрицей
размера 20 х 20, в которой все элементы главной диагонали равны нулю, а
все остальные элементы равны либо 2 (выигрыш), либо 0(проигрыш), либо 1
(ничья).
(1) подсчитать количество участников турнира, не потерпевших ни одного
поражения;
(2) найти количество участников турнира, набравших более 50% очков,
т.е. более 9.5 очков;
(3) определить номера всех участников, которые имели больше побед,
чем поражений;
(4) упорядочить участников турнира в порядке неубывания набранных ими
очков;
(5) найти самых сильных и самых слабых участников турнира;
(6) определить, есть ли среди участников трое таких, что первый выиграл
у второго, второй -- у третьего, а третий -- у первого.
23. Для заданной литерной матрицы A размером 40х50 определить
(1) номера строк, в которых нет цифр, либо встречается хотя бы одна
из букв "а", "о", "е" до первой цифры;
(2) номера столбцов, содержащих по крайней мере два пробела и по одной
каждой из букв;
(3) количество строк, в которых нет ни одной четной цифры, но есть
хотя бы один из знаков "+", "-" или "!";
(4) количество столбцов, в которых все символы попарно различны.
24. Дана целочисленная матрица размера nxn, элементы которой
положительны и расположены в каждой строке и в каждом столбце по неубыванию.
По заданному числу 
(1) проверить, есть ли число  в матрице;
в матрице;
(2) вычислить сумму элементов каждого квадрата матрицы размера  на
на  ;
;
(3) найти наименьшее целое положительное число, отличное от всех сумм
элементов подпоследовательностей  -й
строки матрицы;
-й
строки матрицы;
(4) проверить, есть ли в каждом столбце хотя бы одно число из отрезка
целых от  до 2m;
до 2m;
(5) найти "пересечение" первого и  -го
столбцов матрицы, т.е. последовательность целых чисел, состоящую из общих
элементов указанных столбцов (причем кратность повторения числа в последовательности
равна минимуму из его кратности в столбцах);
-го
столбцов матрицы, т.е. последовательность целых чисел, состоящую из общих
элементов указанных столбцов (причем кратность повторения числа в последовательности
равна минимуму из его кратности в столбцах);
(6) найти общий элемент строк матрицы с номерами 1,  и
и 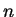 ,
если известно, что 1<
,
если известно, что 1<  <
< 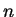 и общие элементы указанных строк существуют;
и общие элементы указанных строк существуют;
(7) проверить, если ли общий элемент у строк с номерами 1,  ,
, 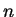 ,
1<
,
1<  <
< 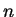 ;
;
(8) найти такой элемент x в первом столбце и такой элемент y
в последнем столбце, чтобы сумма x+y была бы наиболее близка к  .
.
25. В качестве допустимого возьмем одно из следующих преобразований
целочисленной матрицы:
(1) перестановка любых двух строк,
(2) перестановка любых двух столбцов,
(3) замена любого столбца на нулевой,
(4) замена любой строки на последовательность единиц,
(5) замена в любой строке всех нечетных элементов нулями,
(6) замена в любом столбце всех четных элементов числом пять,
(7) замена любой строки на строку, непосредственно ей предшествующую,
(8) замена любого столбца на столбец, непосредственно ему предшествующий,
(9) замена любого столбца на последовательность, содержащую не более
двух нечетных чисел,
(10) замена в любой строке произвольных трех элементов на любое нечетное
число,
(11) замена в любом столбце произвольного элемента на номер столбца,
(12) замена любой строки на первый столбец,
(13) замена любого столбца на последнюю строку,
(14) замена любой строки на произвольную неубывающую последовательность,
(15) замена любого столбца на произвольную возрастающую последовательность.
По заданным двум целочисленным матрицам размера 35x35 определить, можно
ли с помощью допустимых преобразований перейти от первой матрицы ко второй.
26. Найти максимальное из чисел, встречающихся в заданной матрице более
одного раза.
27. Расстояние между k-й и l-й строками целочисленной
матрицы  размера 40 на 40 определяется как
размера 40 на 40 определяется как 
В заданной матрице A найти
(1) номер строки, максимально удаленной от первой;
(2) номера двух наиболее удаленных строк;
(3) строку, равноудаленную от первой и последней.
28. Определить норму заданной матрицы  ,
т.е. число
,
т.е. число 
29. Начиная с центра, обойти по спирали все элементы квадратной матрицы
размером 13 x 13 (распечатывая их в порядке обхода).
30. По заданной квадратной матрице размером 10 x 10 построить вектор
длиной 19, элементы которого -- максимумы элементов, диагоналей, параллельных
главной диагонали.
31. Две строки целочисленной матрицы назовем похожими, если совпадают
множества чисел, встречающихся в этих строках. Найти размер максимального
по числу элементов множества попарно непохожих строк заданной матрицы.
32. Характеристикой строки целочисленной матрицы назовем сумму
ее положительных четных элементов. Переставляя строки заданной матрицы,
расположить их в соответствии с ростом характеристик.
33. Построить целочисленную матрицу  размером
10 x 10 следующим образом:
размером
10 x 10 следующим образом:

где  --
число сочетаний из
--
число сочетаний из 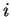 элементов по j.
элементов по j.
34. Найти номер строки заданной целочисленной матрицы размером 10 x
10, в которой находится самая длинная серия.
35. Для заданной целочисленной матрицы найти максимум среди сумм элементов
диагоналей, параллельных главной диагонали матрицы.
36. Для заданной целочисленной матрицы найти минимум среди сумм модулей
элементов диагоналей, параллельных побочной диагонали матрицы.
37. По целочисленной матрице  размером 10 x 10 построить матрицу
размером 10 x 10 построить матрицу 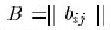 того же размера, элемент
того же размера, элемент которой
равен минимальному элементу треугольника в A, определяемого элементом
которой
равен минимальному элементу треугольника в A, определяемого элементом  :
:

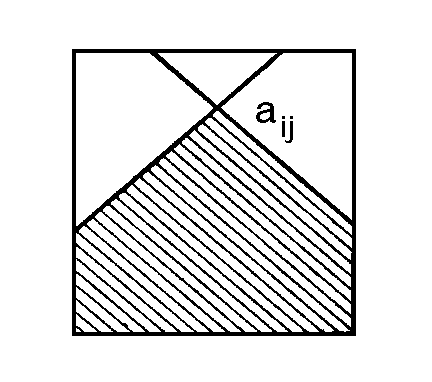
38. По целочисленной матрице  размером 10 x 10 построить матрицу
размером 10 x 10 построить матрицу 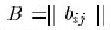 того же размера, где
того же размера, где  определяется следующим образом. Через
определяется следующим образом. Через  проведем в A диагонали, параллельные главной и побочной диагоналям;
проведем в A диагонали, параллельные главной и побочной диагоналям;  определяется как максимум в заштрихованной части матрицы A.
определяется как максимум в заштрихованной части матрицы A.
39. Дана матрица A размером 20 x 20. Считая ее составленной
из 100 квадратов размером 2 x 2 и переставляя эти квадраты, преобразовать
A так, чтобы в результирующей матрице для всяких двух квадратов 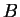 и C выполнялось следующее условие: если сумма элементов
и C выполнялось следующее условие: если сумма элементов 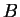 меньше суммы элементов C, то
меньше суммы элементов C, то 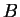 лежит либо выше, либо левее (когда
лежит либо выше, либо левее (когда 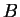 и C на одной горизонтали) квадрата C.
и C на одной горизонтали) квадрата C.
40. Дан текст -- последовательность литер длины не более 10000. Последовательность
содержит русские буквы, пробелы, знаки препинания -- запятую, точку с запятой,
двоеточие, круглые скобки, вопросительный и восклицательный знаки, -- и
заканчивается точкой. Слова -- это серии букв, отделенные друг от друга
в этой последовательности пробелами или знаками препинания. Известно, что
каждое слово содержит не более 20 букв. Построить
(1) словарь, содержащий все различные слова текста (представить его
литерной матрицей);
(2) лексикографически упорядоченный словарь, содержащий все различные
слова текста;
(3) 10 самых частых слов, с упорядочением по невозрастанию числа их
вхождений в текст и указанием этих количеств вхождений.
41. Найти максимальный среди всех элементов тех строк заданной матрицы,
которые упорядочены (либо по возрастанию, либо по убыванию).
42. Характеристикой столбца целочисленной матрицы назовем сумму
модулей его отрицательных нечетных элементов. Переставляя столбцы заданной
матрицы, расположить их в соответствии с ростом характеристик.
43. Подсчитать количество столбцов заданной целочисленной матрицы размером
20 x 20, которые составлены из попарно различных чисел.
44. Подсчитать количество строк заданной целочисленной матрицы размером
20 x 20, являющихся перестановкой чисел 1,2, ... , 20.
45. Напечатать элементы заданной целочисленной матрицы размером 10 x
10 в порядке неубывания их значений.
46. Напечатать элементы заданной литерной матрицы размером 10 x 10 в
порядке невозрастания их кодов.
47. Среди строк заданной целочисленной матрицы, содержащих только нечетные
элементы, найти строку с максимальной суммой модулей элементов.
48. Среди столбцов заданной целочисленной матрицы, содержащих только
такие элементы, которые по модулю не больше 10, найти столбец с минимальным
произведением элементов.
49. По заданной матрице размером 10 x 10 найти все такие k, что
k-я строка матрицы совпадает с k-м столбцом.
50. Пусть m(A,i) означает номер столбца матрицы A,
в котором находится последний в строке минимум 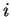 -й
строки. Проверить, верно ли, что для заданной матрицы A размером
20 x 20 выполняются неравенства
-й
строки. Проверить, верно ли, что для заданной матрицы A размером
20 x 20 выполняются неравенства

51. Найти максимальное из чисел, встречающихся в заданной целочисленной
матрице размером 20 х 30 более одного раза (или напечатать текст: "Все
элементы матрицы попарно различны").
52. Всякий элемент  заданной квадратной матрицы
заданной квадратной матрицы  размером 20 x 20 задает разбиение матрицы на четыре клетки с индексами
размером 20 x 20 задает разбиение матрицы на четыре клетки с индексами

 ,
,
хотя бы одна из которых непуста. Построить матрицу 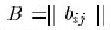 того же размера, в которой
того же размера, в которой  равен минимуму среди максимальных элементов непустых клеток, определяемых
в 209#95 элементом
равен минимуму среди максимальных элементов непустых клеток, определяемых
в 209#95 элементом  .
.
53. Проверить, удовлетворяет ли заданная матрица  размером 10 x 10 следующему условию: для всех i >1 и для всех j
>1 верно неравенство
размером 10 x 10 следующему условию: для всех i >1 и для всех j
>1 верно неравенство 
54. Для двух заданных матриц одинакового размера проверить, можно ли
получить вторую матрицу из первой применением (конечного числа раз) операций
транспонирования (симметричной замены положения всех элементов) относительно
главной и побочной диагоналей.
55. Найти и распечатать строку заданной целочисленной матрицы размером
10 x 10, в которой длина максимальной серии минимальна.
56. Две строки литерной матрицы назовем похожими, если совпадают
множества литер, встречающихся в этих строках. Для заданной литерной матрицы
размером 20 х 30
(1) выделить максимальное множество попарно непохожих строк;
(2) построить (симметричную) логическую матрицу 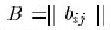 размером 20 х 30, в которой элемент
размером 20 х 30, в которой элемент  равен True тогда и только тогда, когда
равен True тогда и только тогда, когда 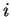 -я
и j-я строки исходной матрицы являются похожими;
-я
и j-я строки исходной матрицы являются похожими;
(3) построить вектор длины 20, в котором i-й элемент равен количеству
строк исходной матрицы (включая 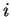 -ю),
похожих на
-ю),
похожих на  -ю
строку.
-ю
строку.
57. Напечатать элементы заданной матрицы размером 10 x 10 в следующем
порядке:


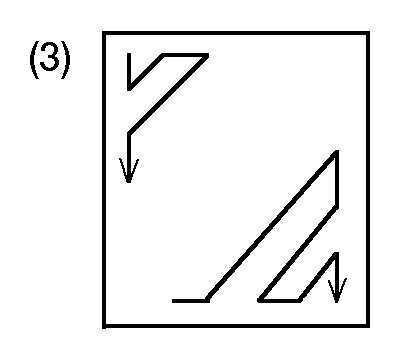
58. Взаимно однозначное отображение элементов матрицы на себя можно
задать с помощью двух целочисленных матриц: в первой указать номер строки,
куда переходит данный элемент, а во второй -- номер столбца. Построить
две матрицы, задающие отражение каждого элемента матрицы размером 10 x
10 на симметричный ему относительно главной диагонали.
Next:5.5
Задания
Up:5.4
Программы обработки матриц
Previous:5.4.4
Поиск номера строки-серии
© В.Н. Касьянов, Е.В.Касьянова,2004









