4.1.5 Пошаговая разработка программ

Уже отмечалось, что разработка программы представляет собой задачу на построение. Поэтому, как обычно в таких случаях (вспомним, например, геометрические задачи на построение из школьной математики), необходим этап анализа задачи. На этом этапе, задавая вопросы: что дано ? и что требуется ? нужно установить классы наборов входных и выходных данных будущего алгоритма, выделить основные необходимые отношения между входными и выходными наборами данных и компонентами этих наборов, выделить подцели, которые нужно достичь для решения задачи, и, как следствие этого, выработать подход к построению алгоритма.

Результатом этого этапа должна быть внешняя спецификация программы, т.е. строгая, точная и понятная формулировка в общем виде того, что (в рамках выбранного подхода -- см. две спецификации программы возведения в десятую степень в п. 2.3.1) должна делать программа, чтобы переработать входные данные в выходные.

Когда внешняя спецификация программы такова, что программисту не удается сразу представить детальный вид программы, с самого начала ее создания можно и нужно придерживаться некоторой дисциплины, позволяющей разбить процесс программирования на ряд последовательных шагов, выделить необходимые подцели каждого шага разработки и проследить взаимосвязь между ними.

Суть этой дисциплины, получившей название метода пошаговой разработки, состоит в том, что программа разрабатывается "сверху вниз", начиная с ее внешней спецификации, что сложная для программирования задача разбивается на несколько более простых подзадач, которые независимо программируются при дальнейшей детализации алгоритма.

При таком методе разработка текста программы происходит по шагам, на каждом из которых принимается небольшое число локальных решений и строится новое (более детальное) законченное описание решения задачи в виде аннотированного алгоритма. Это описание не обязано быть законченной программой на языке Zonnon, а может наряду с фрагментами окончательного вида программы также содержать фрагменты, подлежащие уточнению на следующих шагах разработки программы. Таким образом, получается последовательность все более детальных спецификаций алгоритма, приближающихся к окончательной версии программы.

В качестве иллюстрации рассмотрим применение метода для решения следующей задачи: прочитать непустую последовательность целых чисел и напечатать длину последовательности, наибольшее число в ней и наименьшее ее число. Указанная задача сразу сформулирована как математическая и не содержит сложностей, затрудняющих ее анализ. Ее внешняя спецификация может быть записана следующим образом:

Программа: Длина, максимум и минимум
Вход: $\alpha$
где$\alpha \in Integer^+$
Выход:$K M N$

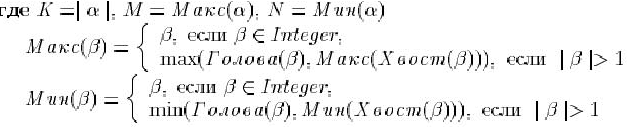
Спецификация не только фиксирует что дано на входе разрабатываемого алгоритма и что требуется получить, но и описывает метод, который может быть реализован этим алгоритмом. Теперь задача состоит в написании программного текста, который из любых состояний, удовлетворяющих предусловию (дано), переводит ВМ в состояние, удовлетворяющее постусловию (получить). В соответствии со спецификацией решение задачи можно представить в виде:

module ДлинаМаксимумМининмум;
    var K,M,N : integer;
begin Прочитать первое входное число A и присвоить переменным
         M, N, K значения A, A и 1 соответственно;
         (* $\{M$ = Макс(Input1), $N$ = Мин(Input1), $K = \mid Input1 \mid = 1\}$ *)
         Если не пуста последовательность $\beta$ непрочитанных чисел, т.е. $\mid Input2\mid > 0,$
         то прочитать ее всю, присвоив переменным M, N, K значения
         выражений $\max(M,$Макс$(\beta))$, $\min(N,$Мин$(\beta))$, $K+\mid \beta \mid$;
         (* $\{\mid Input2 \mid = 0, M =$Макс$(Input),$$N =$Мин(Input)$, K = \mid Input \mid \}$*)
        Напечатать значения К, M и N;
end ДлинаМаксимумМининмум.

Тем самым исходная задача оказалась разбита на три подзадачи, оформленные в виде фрагментов программы, являющихся словесными операторами. Для каждой из подзадач известны предусловие и постусловие; в частности, дано является предусловием первой подзадачи, а получить -- постусловием третьей подзадачи. Подзадачи можно теперь обдумывать и реализовывать независимо, применяя тот же самый подход, т.е. описывая их на языке Паскаль или, если они сложны для прямого решения, разбивая их на подзадачи и т.п.

В частности, наша программа состоит из трех последовательно работающих операторов, первый и последний из которых просты для реализации. Первый оператор может быть реализован следующей последовательностью операторов

    read(N); M := N; K := 1 ,

а последний -- оператором

    write (K, M, N).

В результате этих двух шагов уточнения получаем программу на языке Zonnon за исключением одного оператора, реализовать который можно оператором цикла с условием на продолжение:

    while ~ Eof do (* {Ограничивающее выражение: $\mid Input2 \mid \}$ *)
        (*$\{\mid Input2 \mid > 0, M$ = Макс(Input1), $N$ = Мин(Input1), $K = \mid Input1 \mid \}$ *)
        Ввести первое непрочитанное входное число В, присвоив переменным M, N, K
        значения выражений $\max(M,B)$, $\min(N,B)$, $K+1$ ;
        (* {M = Макс(Input1), $N$ = Мин(Input1), $K = \mid Input1 \mid \}$ *)
    end.

Телом этого оператора цикла является оператор, требующий уточнения. Зафиксировав переменную $Х$ для хранения только что прочитанного элемента входной последовательности (и добавив ее описание!), можно реализовать этот оператор следующей последовательностью операторов

     read(X);
     K :=K+1;
     Присвоить переменным M и N значения max(M,X) и min(N,X);
 

Последующие уточнения очевидны и приводят к программе, общий вид которой изображен ниже. Здесь словесные операторы, уточняемые на последующих шагах построения программы, сохраняются в программе в виде комментариев. Чтобы их отличать от комментариев-утверждений, описывающих свойства состояний программы в точках их расположения, словесные операторы не даются курсивом.

module ДлинаМаксимумМининмум;
    var K,M,N : Integer; X : integer;
begin
    (*Прочитать первое входное число A и присвоить переменным M, N, K
    значения A, A и 1 соответственно;*)
    read(N); M := N; K := 1;
    (* $\{M =$Макс(Input1), $N$ = Мин(Input1),$K = \mid Input1 \mid = 1$*)
    (*Если не пуста последовательность $\beta$ непрочитанных чисел, т.е.$\mid Input2\mid > 0,$ то прочитать ее всю,
    присвоив переменным M, N, K значения выражений $\max(M, Макс(\beta))$, $\min(N,$Мин$(\beta))$, $K+\mid \beta \mid$;*)
    while ~ Eof do (*{Ограничивающее выражение: $\mid Input2 \mid \}$*)
        (*{M=Макс(Input1), $N =$Мин(Input1), $K = \mid Input1 \mid \}$*)
        (*Ввести первое непрочитанное входное число В, присвоив
        переменным M, N, K значения выражений $\max(M,B)$, $\min(N,B)$, $K+1$;*)
        read(X); K :=K+1;
        (*Присвоить переменным M и N значения max(M,X) и min(N,X);*)
        if X $>$ M then M := X elseif X $<$ N then N := X end
        (*{ M= Макс(Input1), $N =$Мин(Input1), $K = \mid Input1 \mid \}$*)
    end;
    (*$\{\mid Input2 \mid = 0, M$= Макс(Input), $N$ = Мин(Input), $K = \mid Input\mid \}$*)
    (*Напечатать значения К, M и N;*)
    write (K, M, N)
end ДлинаМаксимумМининмум.

Важно отметить, что окончательный текст Zonnon-программы содержит весь ход ее разработки (это позволяет любому пользователю программы при желании повторить шаги уточнения алгоритма и убедиться, что программа правильна по построению). Ясно, что программа будет тем лучше понята и будет иметь тем больше шансов быть правильной, чем меньше "размеры" шагов уточнения и чем в большей степени эти шаги снабжаются точными утверждениями и строгими рассуждениями, демонстрирующими их корректность (для цикла, например, должны быть приведены и доказаны инварианты и условия завершения). Вместе с тем следует признать, что современные формальные методы доказательства невозможно систематически применять ко всем элементам большой программы. Напротив, можно рекомендовать достижение при программировании некоторого разумного компромисса между интуицией и формальной строгостью. Во многих местах программы можно ограничиться лишь набросками проведенных доказательств, но не в ущерб точности изложения и правильности разработанной программы. Особенно строго нужно разрабатывать "тонкие" места программы, с особым вниманием относясь к циклам.
 

© В.Н. Касьянов, Е.В.Касьянова, 2004