где
Выход:
где
Программа: Суммирование элементов последовательности
Вход: ![]()
где![]()
Выход: ![]()
где![]() = Сумма
= Сумма![]()
![]()
Решением задачи является следующая "программа", длина которой не может быть ограничена из-за отсутствия ограничения на длину входной последовательности:
module СуммаЭлементовПоследовательности;
var СУММА,ЭЛЕМ : real;
begin
СУММА := 0; (* { СУММА = Сумма (Input1), ![]() *)
*)
if ~ Eof then
read
(ЭЛЕМ); СУММА := СУММА + ЭЛЕМ
(* {СУММА = Сумма(Input1), ![]() *)
*)
if ~ Eof then
read (ЭЛЕМ); СУММА := СУММА + ЭЛЕМ
(* {СУММА = Сумма(Input1), ![]() *)
*)
![]()
end
end;
(* {СУММА = Сумма(Input1), ![]() *)
*)
write(СУММА)
end СуммаЭлементовПоследовательности.
В языке Zonnon такую неограниченную вложенность условных операторов
можно представить в виде одного оператора цикла с условием на продолжение,
синтаксис которого представлен на рис. 4.1.
WhileStatement = while Expression do StatementSequence end.
Рис. 4.1. Синтаксис оператора цикла с условием на продолжение
Пусть B обозначает некоторое логическое выражение, а ![]() -- последовательность операторов. Тогда действие, выражаемое оператором
-- последовательность операторов. Тогда действие, выражаемое оператором
while B do S end,
можно представить как
if B then S; while B do S end end,
т.е., следуя данному оператору, ВМ проверит истинность логического выражения ![]() ;
если на текущем состоянии памяти B истинно, то выполнится последовательность
операторов
;
если на текущем состоянии памяти B истинно, то выполнится последовательность
операторов ![]() ,
затем опять проверится истинность B, но уже на новом текущем состоянии
памяти, и опять выполнится последовательность операторов
,
затем опять проверится истинность B, но уже на новом текущем состоянии
памяти, и опять выполнится последовательность операторов ![]() ,
если B
,
если B![]() истинно; и так будет продолжаться (повторяться) перевычисление оператором
истинно; и так будет продолжаться (повторяться) перевычисление оператором ![]() текущего состояния памяти до тех пор, пока первый раз выражение B
не станет ложным. Управляющая структура оператора цикла while B
do
S end, в котором
текущего состояния памяти до тех пор, пока первый раз выражение B
не станет ложным. Управляющая структура оператора цикла while B
do
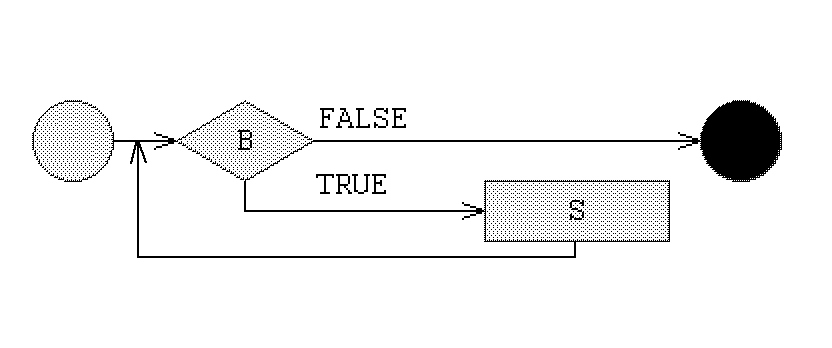
S end, в котором ![]() называется телом цикла, а while B do -- заголовком
цикла, описывается блок-схемой рис. 4.2.
называется телом цикла, а while B do -- заголовком
цикла, описывается блок-схемой рис. 4.2.
 |
Используя оператор цикла, программу![]() СуммаЭлементовПоследовательности
можно
переписать т как:
СуммаЭлементовПоследовательности
можно
переписать т как:
module СуммаЭлементовПоследовательности1;
var СУММА,ЭЛЕМ : real;
begin СУММА := 0; (* {СУММА = Сумма(Input1), ![]() *)
*)
while ~ Eof do
(* {СУММА = Сумма(Input1), ![]() *)
*)
read(ЭЛЕМ); СУММА := СУММА + ЭЛЕМ
(* {СУММА = Сумма(Input1), ![]() *)
*)
end;
(* {СУММА = Сумма(Input) }*)
write (СУММА)
end СуммаЭлементовПоследовательности1.
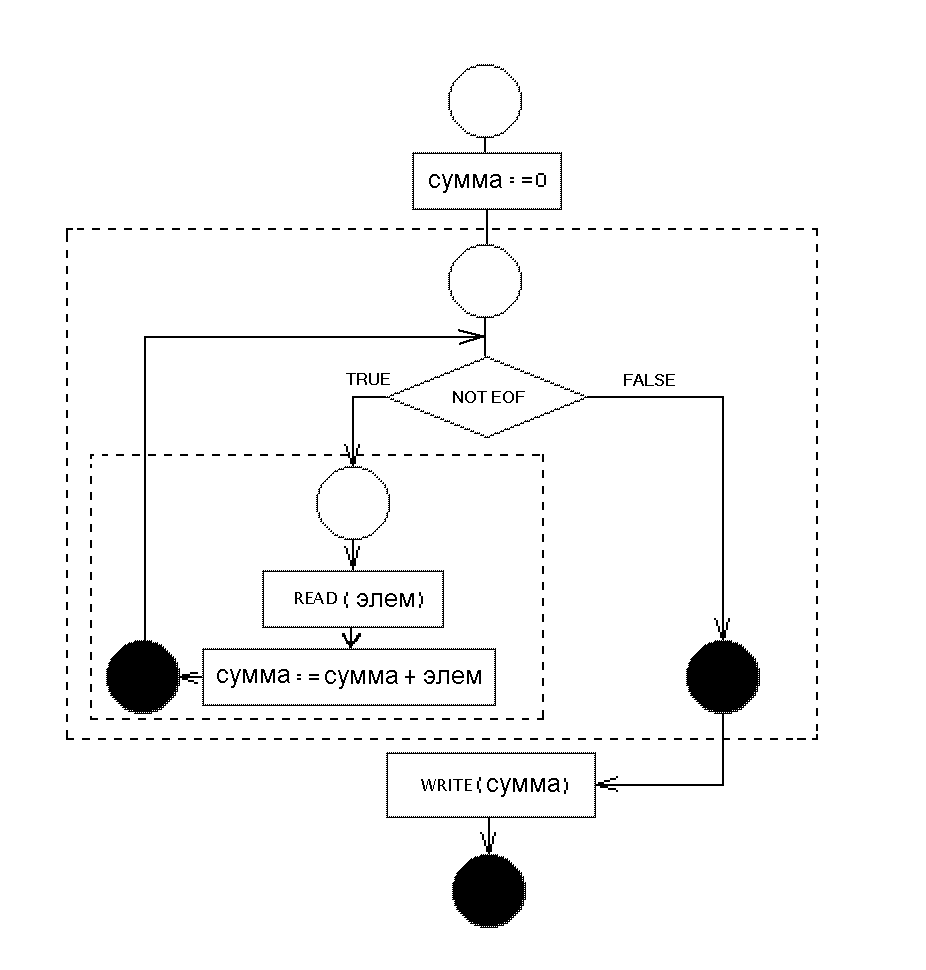
Блок-схема этой программы приведена на рис. 4.3. В ней штриховыми линиями выделены все ее структурные операторы.
 |
Теперь у нас имеется достаточно средств, чтобы записать на языке Zonnon алгоритм Евклида, рассмотренный п.1.1.3:
module НаибольшийОбщийДелитель;
var A,B,C : integer;
begin
read (A,B); (* {A>0, B>0}
*)
while A # B do
if A < B then C := A; A := B; B := C end;
A := A - B
end;
write(A)
end НаибольшийОбщийДелитель.
Next:4.1.2
Свойства оператора цикла
Up:4.1
Средства для организации
Previous:4.1
Средства для организации