
Next:4.5
Обработка последовательности последовательностей
Up:4.4
Функции на последовательностях
Previous:4.4.2
Количество максимумов
4.4.3 Упражнения
1. Даны натуральное число 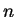 и вещественные числа
и вещественные числа 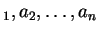 .
Вычислить:
.
Вычислить:
(1) 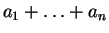 ,
,
(2) 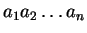 ,
,
(3) среднее арифметическое 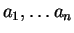 ,
,
(4) среднее геометрическое 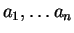 ,
,
(5) 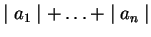 ,
,
(6) 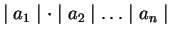 ,
,
(7) 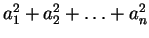 ,
,
(8)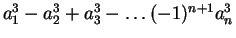 ,
,
(9)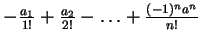 ,
,
(10) 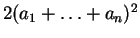 ,
,
(11) 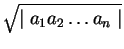 ,
,
(12) 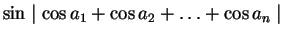 ,
,
(13) 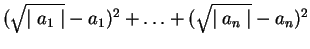 ,
,
(14) 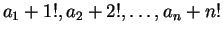 ,
,
(15) 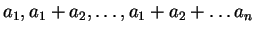 ,
,
(16) 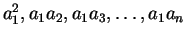 ,
,
(17) 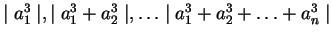 ,
,
(18) 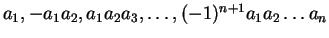 ,
,
(19) 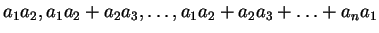 ,
,
(20) 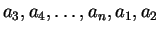 ,
,
(21) 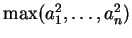 ,
,
(22) 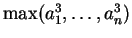 ,
,
(23) 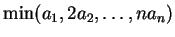 ,
,
(24) 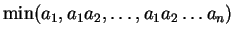 ,
,
(25) количество четных среди 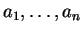 ,
,
(26) количество удвоенных нечетных среди 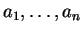 ,
,
(27) количество полных квадратов среди 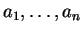 ,
,
(28) количество квадратов нечетных чисел среди 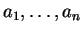 ,
,
(29) количество элементов 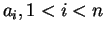 ,
имеющих соседей с различными знаками,
,
имеющих соседей с различными знаками,
(30) количество таких элементов 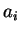 ,
что
,
что 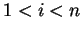 и
и
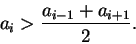
2. Даны натуральное n и вещественные числа 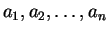 .
Выяснить, образуют ли монотонную (возрастающую или убывающую) последовательность
числа:
.
Выяснить, образуют ли монотонную (возрастающую или убывающую) последовательность
числа:
(1) 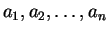 ,
,
(2) 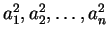 ,
,
(3) 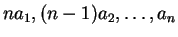 ,
,
(4) 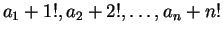 ,
,
(5) 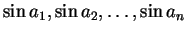 ,
,
(6) 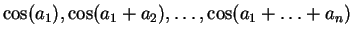 ,
,
(7) 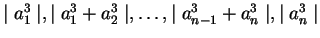 .
.
3. Задана последовательность символов. Определить:
(1) сколько раз в ней встречается буква 'X',
(2) входит ли в нее буква 'Y',
(3) верно ли, что в ней содержатся все буквы, входящие в BEGIN,
(4) имеется ли в ней подпоследовательность букв, образующих слово DO
или слово IF,
(5) верно ли, что в ней количество вхождений арифметических операций
превышает количество вхождений цифр,
(6) сколько букв встречается в ней между первым и вторым двоеточием,
(7) длину наибольшей серии подряд идущих пробелов,
(8) сколько цифр предшествует первой букве.
4. Преобразовать заданную последовательность символов, заменив в ней:
(1) все символы, не являющиеся буквами и цифрами, их номерами в литерном
типе (т.е. последовательностями цифр, составляющих эти номера),
(2) каждую точку, предшествующую первой запятой, многоточием (т.е.
тремя точками),
(3) каждую из групп стоящих рядом точек одной точкой,
(4) каждую группу букв ONE группой букв TWO,
(5) на пробел каждый арифметический знак, перед которым есть хотя бы
одна буква.
5. Преобразовать заданную последовательность символов, удалив из нее
(1) все предшествующие первой точке символы, не являющиеся буквами,
(2) все следующие за первой запятой четные цифры,
(3) группы символов, расположенные между скобками (и), вместе с этими
скобками (Предполагается, что внутри скобок нет других скобок),
(4) все запятые, предшествующие второй точке (если двух точек нет,
то все запятые), и заменив в ней знаком '+' все цифры, которым предшествует
ровно одна точка (например, последовательность "A1,2,3!" преобразуется
в "A123!", а "A,1,.,B,2C,.,D3.,E4" -- в "A1.B+C.,D3.,E4").
(5) все группы слов АВВА.
6. Определить количество составных операторов в заданной Паскаль-программе,
не содержащей комментариев.
7. Определить максимальную глубину вложенности составных операторов
в заданной Паскаль-программе, не содержащей комментариев и операторов выбора.
8. Пусть по некоторому каналу передается сообщение, имеющее вид последовательности
точек и тире. Поскольку из-за помех возможен ошибочный прием некоторых
сигналов (точка может быть воспринята как тире или наоборот), при передаче
каждый сигнал повторяется трижды, а при приеме три последовательные символа
расшифровываются тем символом, который среди них встречается по крайней
мере дважды. Написать программу расшифровки.
9. Зашифровать сообщение, заданное последовательностью 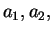
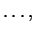
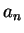 точек и тире, построив по нему последовательность
точек и тире, построив по нему последовательность 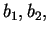
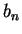 ,
образованную по следующим правилам:
,
образованную по следующим правилам:
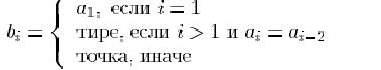
Next:4.5
Обработка последовательности последовательностей
Up:4.4
Функции на последовательностях
Previous:4.4.2
Количество максимумов
© В.Н. Касьянов, Е.В.Касьянова, 2004