(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
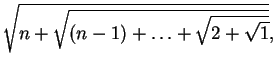
(12)
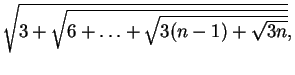
(13)
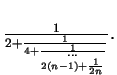
Next:4.4
Функции на последовательностях
Up:4.3
Программы вычисления элемента последовательности
Previous:4.3.3
Схема Горнера
(1) ![]() ,
,
(2) ![]() ,
,
(3) ![]() ,
,
(4) ![]() ,
,
(5) ![]()
(6) ![]()
(7) ![]() для нечетного n и
для нечетного n и![]() для четного
для четного ![]()
(8) ![]() для четного n и
для четного n и ![]() для нечетного
для нечетного ![]()
(9) ![]()
(10) ![]()
(11) 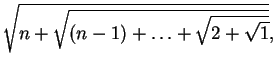
(12) 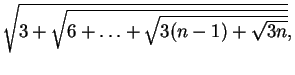
(13) 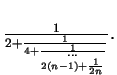
2. Даны целое число n и вещественное число х. Вычислить
(1) ![]() ,
,
(2) ![]() ,
,
(3) ![]() ,
,
(4) ![]() ,
,
(5) ![]() ,
,
(6) ![]() ,
,
(7) ![]() ,
,
(8) ![]() ,
,
(9) 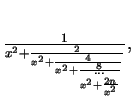
(10) ![]()
(11) ![]() ,
,
(12) ![]() .
.
3. Дано натуральное число ![]() .
Определить
.
Определить
(1) количество цифр в числе ![]() ,
,
(2) сумму квадратов цифр числа ![]() ,
,
(3) первую четную цифру в изображении числа ![]() ,
,
(4) все меньшие ![]() простые числа,
простые числа,
(5) есть ли среди чисел ![]() ,
, ![]() +1,
+1,![]() ,
2
,
2![]() такие, запись которых совпадает с последними цифрами записи их квадрата
(как, например, 6
такие, запись которых совпадает с последними цифрами записи их квадрата
(как, например, 6![]() = 36, 25
= 36, 25![]() = 625 и т.д.),
= 625 и т.д.),
(6) наименьшее число Армстронга, принадлежащее интервалу [1,![]() ].
(Натуральное число из
].
(Натуральное число из ![]() цифр является числом Армстронга, если сумма его цифр, возведенных в
цифр является числом Армстронга, если сумма его цифр, возведенных в ![]() -ю
степень, равна самому числу, как, например, 153 = 1
-ю
степень, равна самому числу, как, например, 153 = 1![]() + 5
+ 5![]() + 3
+ 3![]() ),
),
(7) можно ли его преобразовать в число 1, повторяя не более ![]() раз следующие действия: если число четно, то разделить его на 2, иначе
умножить число на 3 и прибавить 1,
раз следующие действия: если число четно, то разделить его на 2, иначе
умножить число на 3 и прибавить 1,
(8) в порядке возрастания ![]() первых натуральных чисел, которые не делятся ни на какие простые числа
кроме 2, 3 и 5,
первых натуральных чисел, которые не делятся ни на какие простые числа
кроме 2, 3 и 5,
(9) последовательность последних ![]() десятичных цифр числа
десятичных цифр числа ![]() ,
,
(10) двоичное представление числа ![]() ,
т.е. такую последовательность
,
т.е. такую последовательность ![]() нулей и единиц, что
нулей и единиц, что ![]() и
и ![]() ,
,
(11) последовательность ![]() ,
каждый член которой равен -1, 0 или 1, такую, что
,
каждый член которой равен -1, 0 или 1, такую, что
![]() и
и ![]() .
.
(12) такое натуральное число m, что запись числа ![]() получается из записи m изменением порядка цифр на обратный,
получается из записи m изменением порядка цифр на обратный,
(13) сколько раз каждая цифра встречается в записи числа ![]() .
.
4. Даны натуральное число ![]() и положительные вещественные числа
и положительные вещественные числа ![]() .
Найти
.
Найти ![]() первых таких членов
первых таких членов ![]() ,
для которых
,
для которых ![]() ,
в последовательности
,
в последовательности ![]() ,
образованной по следующим правилам:
,
образованной по следующим правилам:
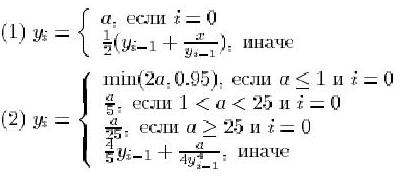
5. Дано натуральное n. Вычислить ![]() -е
элементы последовательностей
-е
элементы последовательностей ![]() и
и ![]() ,
построенных по следующим правилам:
,
построенных по следующим правилам:
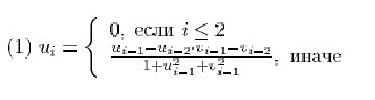
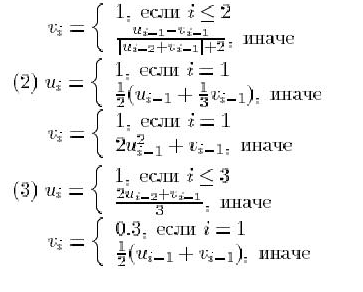
Next:4.4
Функции на последовательностях
Up:4.3
Программы вычисления элемента последовательности
Previous:4.3.3
Схема Горнера