4.2.3 Упражнения

1. Задана последовательность вещественных чисел четной длины. Предполагая, что каждая пара чисел задает границы отрезка на числовой оси, указать те отрезки, которые содержат четное число.

2. Даны целое число $n$$\geq$ 0 и последовательность целых чисел a$а_1$, a$а_2$,$\ldots$,a$а_n$. Найти те члены $a_i$ последовательности, которые

(1) являются удвоенными нечетными числами;
(2) при делении на 11 дают остаток 1, 2 или 5;
(3) обладают тем свойством, что уравнение x$х^2 + ix + a_i$ имеет два действительных корня;
(4) кратны 7 и не кратны 5;
(5) являются квадратами четных чисел;
(6) имеют четные порядковые номера и являются нечетными числами;
(7) являются степенями двойки;
(8) являются номерами букв в литерном типе;
(9) не являются номерами цифр в литерном типе;
(10) принадлежат интервалу [-i,i];
(11) являются простыми числами;
(12) совпадают с последними цифрами записи их квадрата (как, например, $6^2 = 36$, $25^2 = 625$ и т.д.);
(13) состоят из трех цифр и совпадают с суммой своих цифр, возведенных в третью степень (как, например,
153 = $1^3 + 5^3 + 3^3$);
(14) состоят из трех цифр и читаются одинаково с начала и с конца (как, например, 151, 212 и т.д.).

3. Пусть вещественные числа a,b и функция y = f(x) имеют следующий вид:

(1) y = sin x + cos x, a= 0, b = $\pi$,
(2) y = 2 sin x + 3 cos x, a = -$\pi$, b = $\pi$,
(3) y = x$^4$ + 1, a = -1, b = 2,
(4) y = $\frac {1}{x^2 - x + 1}$, a = -1, b = 3,
(5) y = $\frac {x-3}{x^2 +2}$, a = -1, b = 4,
(6) y = $x^2e^{-\mid x \mid}$, a = -1, b = 4,
(7) y = $e^{-x}$ sin 2x, a = - $\frac{\pi}{2}$, b = 2,
(8) y = $\sqrt[3]{(x+2)^2} - \sqrt[3]{(x-2)^2}$, a = -3, b = 3.

По заданному натуральному числу $n, n>0,$ построить график функции $y = f(n)$ на отрезке $[a,b]$, вычислив значения функции в точках $a, a+h, a+2h, \ldots, b,$ где $h = \frac{b-a}{n}.$ Ось абсцисс расположить вертикально, а ось ординат горизонтально. Шаг по оси абсцисс -- это переход на новую строку, шаг по оси ординат -- позиция следующего символа в текущей строке. Точки графика изображать символом "$*$".

4. Даны целое число $n, n\geq 0,$ и последовательность вещественных чисел $a_1, a_2,\ldots, a_n$.

(1) В последовательности $a_1, a_2,\ldots, a_n$ заменить каждый из $i-$й член $a_i$ остатком от деления его квадрата на $i$.
(2) Получить "сглаженные" значения $a_1, a_2,\ldots, a_n$, заменив в исходной последовательности все члены, кроме первого и последнего, на новые элементы $b_i$, вычисляемые по формуле $b_i = \frac{1}{3} (a_{i-1} + a_i + a_{i+1})$.
(3) Решить предыдущую задачу "сглаживания", считая, что $b_i = \frac{1}{3} (b_{i-1} + a_i + a_{i+1})$.

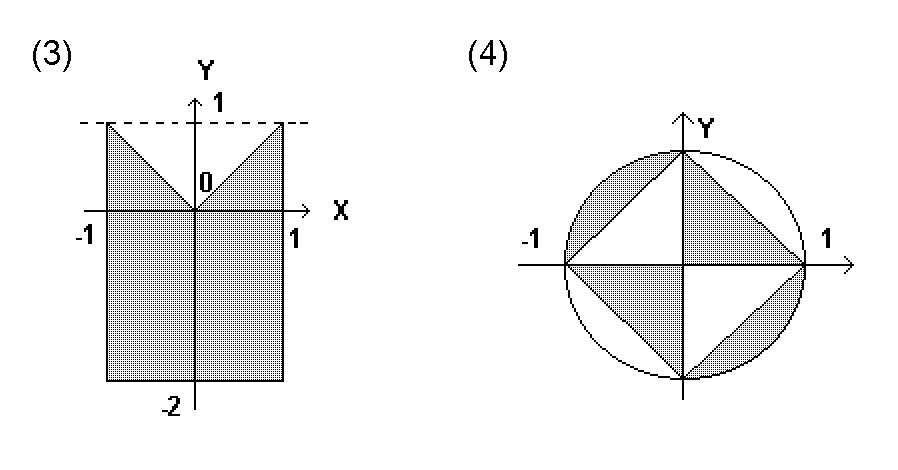
5. Дана последовательность вещественных чисел четной длины. Рассматривая пары соседних чисел в качестве координат точек, определить, принадлежат ли все заданные точки заштрихованной части плоскости рис. 4.7.

Рис. 4.7. Области плоскости

6. Даны натуральное число $n$ и вещественное число $r$. Вычислить координаты вершин правильного $n$-угольника, вписанного в окружность радиуса $r$ с центром в начале координат.

7. Даны натуральные числа $А,В,С$ и последовательность координат точек, являющихся также натуральными числами. Определить

(1) какие из заданных точек лежат внутри окружности радиуса $А$ с центром в точке (B,C),
(2) сколько заданных точек лежит вне окружности радиуса $А$ с центром в начале координат, но между прямыми y=B и y=C,
(3) есть ли такой отрезок, соединяющий две соседние точки, который бы пересекал окружность радиуса $А$ с центром в точке (B,C).

8. Прямая на плоскости задается уравнением $ах + by + c = 0$, где $a$ и $b$ одновременно не равны нулю. Пусть задана последовательность целых чисел $a_1, b_1, c_1, a_2, b_2,c_2,\ldots, a_n, b_n, c_n$, образованная из коэффициентов $n$прямых, где $n \geq 3$. Определить

(1) все прямые, которые параллельны первой из заданных прямых,
(2) верно ли, что все прямые пересекают первую из заданных прямых,
(3) прямые, перпендикулярные первой или второй из заданных прямых,
(4) количество прямых, расположенных над первой прямой и не пересекающих вторую,
(5) углы, под которыми каждая прямая, не параллельная первой прямой, пересекает первую прямую.

9. Дана последовательность вещественных чисел $a_1, a_2,\ldots, a_n$, длина которой кратна трем. Каждая тройка чисел $a_i, a_{i+1},a_{i+2}$, где $i$ кратно трем, задает центр круга $(a_i,a_{i+1})$ и его радиус $a_{i+2}$. Найти те круги, которые

(1) содержат точку начала координат;
(2) касаются одной из осей координат;
(3) пересекаются с прямой y = x.

10. Зашифровать заданный текст, заменив в нем каждую букву непосредственно следующей за ней по алфавиту (буква "Z" заменяется на "А"). Остальные символы текста изменяются по следующему правилу: "." переходит в "!", "," -- в ".", ";" -- в "+", "?" -- в "-", "!" -- в "$*$".

11. Преобразовать заданную последовательность символов,

(1) заменив в ней все восклицательные знаки вопросительными,
(2) заменив каждую запятую и точку многоточием (т.е. тремя точками),
(3) удалив из нее все символы, не являющиеся буквами,
(4) удалив из нее все четные цифры,
(5) удалив из нее все запятые и заменив точкой все цифры.

12. Выяснить, можно ли представить факториал каждого натурального числа из заданной последовательности в виде произведения трех последовательных натуральных чисел.
 

© В.Н. Касьянов, Е.В.Касьянова, 2004