2.1.3 Логический тип (Boolean)

2.1.3 Логический тип (boolean)

Next:2.1.4 Тип целый (integer)
Up:2.1 Стандартные типы данных
Previous:2.1.2 Операции и стандартные функции

A $\vee$ B

A $\wedge$ B

A $\leftrightarrow$ B

Тип boolean состоит из двух логических значений, имеющих стандартные имена true (истина) и false (ложь).

Само название типа происходит от имени Дж.Буля (G.Boole, 1815-1864), заложившего основы алгебры логики, часть сведений о которой мы кратко напомним.

В математике для логических значений обычно используются обозначения 1 (истина) и 0 (ложь) и рассматривается следующий набор функций: дизъюнкция -- $\vee$ (или), конъюнкция -- $\wedge$ (и), отрицание -- $\neg$ (не), импликация -- $\to$ (следует) и эквивалентность -- $\leftrightarrow$ (тогда и только тогда). Эти функции можно задать следующей таблицей:

Из этой таблицы можно вывести следующие законы (тавтологии) -- формулы, принимающие истинные значения при любых логических значениях, взятых в качестве и (а следовательно, и для любых утверждений (утверждение -- это некоторая функция, принимающая логические значения), взятых в качестве и ):

1) законы ассоциативности
$(А\vee (B\vee C)) \leftrightarrow ((A\veeB)\vee C)$
$(A\wedge (B\wedge C)) \leftrightarrow ((A\wedge B) \wedge C)$

2) законы дистрибутивности
$(A\vee (B \wedge C)) \leftrightarrow ((A\veeB)\wedge (A \vee C))$
$(A \wedge (B \vee C))\leftrightarrow ((A \wedge B) \vee (A \wedge C))$

3) законы де Моргана
$(\neg (A \wedge B)) \leftrightarrow ((\neg A)\vee (\neg B))$
$(\neg (A \vee B)) \leftrightarrow ((\neg A)\wedge (\neg B))$

4) закон отрицания $(\neg(\neg A))\leftrightarrow A$

5) закон импликации $(A\to B)\leftrightarrow((\neg A)\vee B)$

6) закон противоречия $(A\wedge(\neg A))\leftrightarrow 0$

7) закон исключенного третьего $(A\vee(\neg A))\leftrightarrow 1$

8) законы упрощения
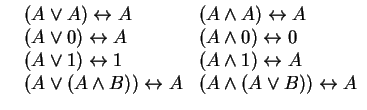
$\begin{array}{ll}\hspace*{3mm} (A\vee A)\leftrightarrow A & (A\wedge A)\lef......))\leftrightarrow A &(A\wedge (A\vee B))\leftrightarrow A \\\end {array}$

9) закон необходимости и достаточности
$(A \leftrightarrow B)\leftrightarrow((A \to B)\wedge (B \to A))$

10) закон вывода следствий
$(A\wedge (A\to B)) \to B$

11) закон транзитивности
$((A\to B)\wedge(B \to C))\to(A \to C)$

12) закон доказательства от противного
$((\neg A) \to 0) \to A$

13) закон доказательства контрпозицией
$(A\to B)\leftrightarrow ((\neg B)\to(\neg A))$ .

В языке Zonnon имеются следующие операции над логическими значениями: or -- дизъюнкция, & -- конъюнкция, ~ -- отрицание.

Next:2.1.4 Тип целый (integer)
Up:2.1 Стандартные типы данных
Previous:2.1.2 Операции и стандартные функции