nextupprevious
Next:2.3.3 Утверждения как множества Up:2.3 Доказательство свойств программ
Previous:2.3.1 Зачем нужны доказательства

2.3.2 Внешняя спецификация программы

При составлении программы мы стремимся к тому, чтобы программа решала некоторую определенную задачу. Понятно, что нельзя доказать правильность программы, если отсутствует ее внешняя спецификация -- достаточно точная и понятная формулировка решаемой задачи. Построение внешней спецификации программы является неотъемлемым этапом пошаговой разработки программ (см. п. 4.1.5), когда хорошие (правильные, надежные, хорошо документированные, легко модифицируемые и достаточно эффективные) программы разрабатываются по шагам, систематическим образом.

Каждая рассматриваемая нами Zonnon-программа реализует некоторую функцию, отображающую множество значений входного файла в множестве значений выходного файла, сопоставляет каждому элементу из области определения функции в точности один элемент из области значений. Поэтому любой "хороший" способ определения реализуемой функции может использоваться в качестве внешней спецификации программы. Рассмотрим небольшой пример.

Пусть имеется задача нахождения максимального из двух натуральных чисел. Внешняя ее спецификация может быть представлена следующим образом:

Программа: Максимальное из двух натуральных чисел
Вход: $N M$
где$N \in$ Integer, $M \in$ Integer, $N \geq 0$, $M \geq 0$
Выход: $L$
где L=Макс(N,M)

Здесь первая строчка (раздел "Программа") содержит название программы. Вторая строчка (раздел "Вход") -- это обозначения для содержимого входного файла в начальном состоянии вычисления, а третья (раздел "где") -- это набор утверждений, описывающих допустимое множество входных данных (допустимы те и только те наборы значений, на которых утверждения принимают истинное значение). Четвертая строчка (раздел "Выход") содержит обозначение содержимого выходного файла в заключительном состоянии вычисления, а пятая и последующие (второй раздел "где") описывают функциональную связь результата программы с ее аргументом. Для записи утверждений и функциональной связи используется язык математики, в том числе системы функциональных равенств (см. п. 1.1.3), а также понятия и конструкции, присутствующие в языке Zonnon. В спецификации ясно и точно указано, что областью определения функции, реализуемой программой, является множество всех пар неотрицательных чисел $N$ и $M$, а также то, что программа должна печатать значение $N$, если $N \geq M$, и M, если N < M.

Заметим, что способ, использованный нами для определения функции $Макс$, является достаточно удобным и наглядным. Вместе с тем, при таком задании область определения функции (множество тех объектов, которые можно подставлять вместо параметров определения; для определения функции $Макс$ параметрами являются $х$ и $у$) и область ее значений даны неявно и не всегда очевидны. То, что функции $Макс$ предполагаются в качестве аргументов произвольные пары неотрицательных целых чисел, выражается в дополнительных ограничениях, а тот факт, что областью значений в этом случае является множество неотрицательных целых чисел, хотя и выводится из правила получения результата функции, тем не менее не выражен явно. Фактически можно считать, что рассмотренное правило задает функцию $Макс$ с существенно более широкими областями определения и значений. Например, в нем явно задано, как получить максимальное из любых двух целых или вещественных чисел. Более точно, правило получения значения функции Макс(N,M) определено для любых таких объектов N$х$ и M, для которых определены операции "$\geq$" и "$<$".

Рассмотрим другой пример. Пусть требуется найти наибольшее из трех вещественных чисел, т.е. требуется построить программу, удовлетворяющую следующей спецификации:

Программа: Наибольшее из трех вещественных чисел
Вход: $N M K$
где$N, M, K \in Real$
Выход: $S$
где  S=Наиб(N,M,K)

   Наиб(x,y,z)=Макс(x,Макс(y,z)),

В общем случае спецификация программы может включать целую систему определений функций, каждое из которых является равенством
 

$f(x_1,\ldots,x_n) = F_1$

или имеет вид

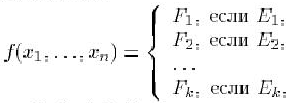
где $n\geq 1$, $k\geq 1$, $x_1,\ldots,x_n$ -- переменные, называемые параметрами определения, $F_1,\ldots,F_к$ -- выражения одного и того же типа (это тип результата определяемой функции $f$), а $ E_1, \ldots, E_k$ -- логические выражения. Предполагается, что выражения $F_1, \ldots, F_к,$$ E_1, \ldots, E_k$, строятся из констант и переменных $x_1,\ldots,x_n$ применением к ним имеющихся в языке операций и стандартных функций, а также функций, определяемых с помощью данной системы определений.

Как уже отмечалось в п. 1.1.3, правила нахождения для конкретных значений c$с_1, \ldots, c_n$ значения функции $f(c_1,\ldots, c_n)$, заданной такими определениями, предполагают подстановку значений $c_i$ вместо параметров $x_i$ в выражения $ E_1, \ldots, E_k$ и нахождение их значений. Если ни одно из логических выражений $ E_1, \ldots, E_k$ не принимает после подстановки истинного значения, то значение $f(c_1,\ldots, c_n)$ не определено. Если же для некоторого $i$ есть выражение E $Е_i$, принимающее значение true, то в качестве значения $f(c_1,\ldots, c_n)$ берется значение выражения, полученного из $F_i$ подстановкой $c_i$ вместо $x_i$.

Нахождение значения некоторого выражения B$В$(например, $E_i$ или $F_i$) осуществляется по шагам, на каждом из которых в B$В$ рассматривается первое слева подвыражение B$В_1$, содержащее только одно применение операции или функции, и делается замена B$В_1$, либо на его значение, если B$В_1$ не содержит определяемых функций, либо на то подвыражение B$В_2$, значение которого определяет значение выражения B$В_1$ в соответствии с определением функции, образующей B$В_1$.

Таким образом, внешняя спецификация рассмотренного вида по существу является программой на языке математических определений, процесс выполнения которой -- это преобразование формул с помощью подстановок.

Следует иметь в виду, что при пошаговой разработке программ качество результирующей программы во многом определяется тем, как мы определим ее внешнюю спецификацию. Рассмотрим две разные спецификации задачи возведения вещественного числа $А$ в десятую степень.
 

Программа: Возведение в десятую степень

Вход: $А$A
где$A \in Real$
Выход: $B$
где
,

.
 

Программа: Быстрое возведение в десятую степень
Вход: A$А$
где A$А \in Real$
Выход: $B$
где

,

.
 

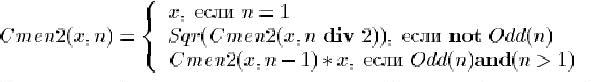Первая спецификация задает процесс преобразований выражений, который соответствует вычислениям по программе $Х$X10 (см. п. 2.2.6), в то время, как вторая описывает идею, лежащую в основе более эффективных программ X10A, X10B, X10C (например, для числа 2 получается следующая последовательность выражений:
B$В$ = Степ$Степ2(2,10)$ = 
= $Sqr(Sqr(4) * 2)$ = $Sqr(16 * 2)$ = $Sqr(32)$ = $1024$.
 

Next:2.3.3 Утверждения как множества Up:2.3 Доказательство свойств программ
Previous:2.3.1 Зачем нужны доказательства

© В.Н. Касьянов, Е.В.Касьянова, 2004