nextupprevious
Next:2.3 Доказательство свойств программ Up:2.2 Выражения, операторы и выражения
Previous:2.2.7 Определяемые функции

2.2.8 Упражнения

1. Указать, какие из следующих выражений не содержат ошибок:

(1) true;
(2) 15;
(3) 3 $<$ X $<$ 5;
(4) $2 \le A$;
(5) A + B = 3;
(6) 3 - Ord(Chr(Abs(X) + 12)));
(7) $A < 3 = B > 4$;
(8) 'A'$>$A;
(9) (Cos X + Sin X) - Z;
(10) Sqrt(X) div5;
(11) (A mod B = 3 + 2) &(A $>$ 3);
(12) Succ(X/Y);
(13) Pred('A');
(14) Succ(Chr(Ord('A')+3)).

2. Пусть A, B, C, D -- переменные целого, вещественного, логического и литерного типа соответственно. Указать, какие из приведенных ниже операторов не содержат ошибок:

(1) C := A $>$ 0;
(2) B := A + 1;
(3) A := B + 2;
(4) D := Chr(A mod 40);
(5) A := Round(B + 2.14);
(6) A := A/3 + 15;
(7) A := Sqrt(A) + 1;
(8) begin end;
(9) begin D := ' D' end;
(10) write(B:A:2);
(11) read(A,B,D),
(12) write(' WRITE' :A);
(13) read(A+1, B+2);
(14) writeln(' A' $>$ D);
(15) begin read(A,B); write(B,A) end.

3. Указать, какие из приведенных ниже программ содержат ошибки.

(1) module A1; var X : real; begin read(X) end A1.

(2) module A2; var A2:real; begin read(A2); write(A2) end A2.

(3) module A3;
        const B ='1'; C = True; D = 3.14; E = 12;
        var F,G : real; H : boolean; K,L : integer; AAAA : integer; BB : char;
        begin writeln (B:10; C:5, D:4:1, E:5);;;; end A3.

(4) module A4; var A: integer; begin READ(A); Write(A) end A4.

(5) module A5 ;
    function C(D:integer): integer;begin return  (D+1) mod 10 end C;
    begin write('ОТВЕТ=',C(15)) end A5.

(6) module A6;
    const R = 10,2;
    var X,Y : real;
    function D(Z,W : real) : boolean;
    begin D := Sqr(Z) + Sqr(W) $>=$ R end D;
    function E(Z:real; W:real) : boolean;
    begin E := (Z$>$0) & (W$<$0) end E;
    begin read(X,Y); write(D(X,Y) & E(X,Y)) end A6.

4. Пусть $А, В$ и $С$ -- переменные целого типа. Указать, какие из следующих операторов решают задачу обмена значениями у $А$A и $В$B:

(1) begin A := B; B := A end,
(2) begin C := A; A := B; B := C end,
(3) begin A := A+B; B := A-B; A := A-B end,
(4) begin C := A; A := B; B := A end.

5. Представить в виде Zonnon-выражений следующие алгебраические выражения:

(1) $-X^Y,$
(2) $\frac{1}{2\cos X} + \ln (\mbox{tg} (\frac{z}{2})) + \frac{12 + 31X}{7,5 - 8X},$
(3) $1 - \frac {\frac {1}{1 + (\frac{R \cdot G}{K})^2}}{\frac {e^2}{s^2} (1 + \frac {R \cdot G}{L})^2)}, $
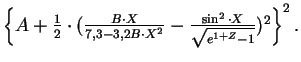
(4) $\left \{A + \frac{1}{2}\cdot ( \frac {B\cdot X}{7,3 - 3,2B\cdot X^2} -\frac {\sin^2\cdot X}{\sqrt{e^{1+Z} - 1}})^2\right \}^2. $

6. Для каждого из следующих выражений определить его тип и типы всех переменных, из которых это выражение составлено:

(1) (A = 'A') or B & (C mod 2 + 1 $>$ D div 3),
(2) Chr(A + B) $>$ D,
(3) Odd(A$*$ B - 1) $>$ C,
(4) (Pred(A) $>$ 'B') or (C mod(D + 1) = E).

7. Пусть $X$ и $Y$ -- две вещественные переменные, используемые для хранения координат точки, а $D$ -- заштрихованная часть плоскости, изображенная на рис. 2. 14.

Записать логическое выражение, принимающее истинное значение тогда и только тогда, когда справедливо высказывание "точка с координатами (X,Y) принадлежит $D$".

Рис. 2.14. Области на плоскости

8. Пусть имеется три вещественных числа A$А$, B$В$ и C$С$. Записать в виде логического выражения высказывание:

(1) существует треугольник со сторонами A$А, В$ B и $С$C;
(2) существует прямоугольный треугольник со сторонами A$А, В$ B и C$С$;
(3) A$А$ является максимумом из чисел A$А, В$B и C$С$, а B$В$ -- минимумом;
(4) если треугольник со сторонами A$А, В$ B и C$С$ существует, то он является остроугольным;
(5) уравнение $АХ^2 + ВХ + С = 0$ не имеет действительных корней.

9. Пусть имеется три литеры A$А, В$ B и C$С$. Записать в виде логического выражения следующие высказывание:

(1) ABC$АВС$ изображают число, кратное семнадцати;
(2) A$А$ является знаком арифметической операции, B$В$ -- четной цифрой, а C -- буквой;
(3) AB$АВ$ изображают номер литеры C$С$ в литерном типе;
(4) либо A$А$ является буквой, а B$В$ не является цифрой, либо одна из литер A$А$ или B$С$ расположена в литерном типе рядом с $В$C.

10. Даны вещественные числа X1, X2, X3, Y1, Y2 и $Y3$. Записать логическое выражение, принимающее истинное значение тогда и только тогда, когда начало координат принадлежит треугольнику с вершинами, имеющими координаты$(X1, Y1), (X2, Y2), (X3, Y3)$.

11. Написать функцию, которая по заданным вещественным числам $X1, X2, X3, X4, Y1, Y2, Y3, Y4$ проверяет:

(1) пересекается ли отрезок, соединяющий вершины с координатами $(X1, Y1), (X2, Y2)$, с отрезком, граничные вершины которого имеют координаты $(X3,Y3)$ и $(X4,Y4)$,

(2) находится ли точка $(X1, Y1)$ внутри треугольника, вершины которого имеют координаты $(X2, Y2), (X3, Y3)$ и $(X4,Y4)$.
 

Next:2.3 Доказательство свойств программ Up:2.2 Выражения, операторы и выражения
Previous:2.2.7 Определяемые функции

© В.Н. Касьянов, Е.В.Касьянова, 2004