Древесная ширина графа
Древесная ширина графа (Treewidth of a graph) — для заданного графа [math]\displaystyle{ G = (V,E) }[/math] древесной декомпозицией называется пара [math]\displaystyle{ (\{X_{i}| \, i \in I\}, T = (I,F)) }[/math], где [math]\displaystyle{ \{X_{i} | \, i \in I\} }[/math] — семейство подмножеств [math]\displaystyle{ V }[/math] и [math]\displaystyle{ T }[/math] — дерево с множеством вершин [math]\displaystyle{ I }[/math] и множеством ребер [math]\displaystyle{ F \subseteq I \times I }[/math] такими, что
- 1) [math]\displaystyle{ \cup_{i \in I} X_{i} = V; }[/math]
- 2) для всех ребер [math]\displaystyle{ (v,w) \in E }[/math] существует [math]\displaystyle{ i \in I }[/math] такое, что [math]\displaystyle{ v \in X_{i} }[/math]и [math]\displaystyle{ w \in X_{i} }[/math]
- 3) для всех [math]\displaystyle{ i, j, k \in I }[/math] таких, что [math]\displaystyle{ j }[/math] лежит на пути в [math]\displaystyle{ T }[/math] из [math]\displaystyle{ i }[/math] в [math]\displaystyle{ k }[/math], справедливо включение [math]\displaystyle{ X_{i} \cap X_{k} \subseteq X_{j} }[/math].
Шириной древесной декомпозиции называется [math]\displaystyle{ \max_{i \in I} |X_{i}| - 1 }[/math]. Древесная ширина графа [math]\displaystyle{ G }[/math] определяется как наименьшая ширина древесной декомпозиции [math]\displaystyle{ G }[/math] и обозначается [math]\displaystyle{ tw(G) }[/math]. В частности, если в этом определении рассматривать не деревья, а пути (точнее, цепи), то получим определение путевой ширины [math]\displaystyle{ pw(G) }[/math].Так как всякий путь есть дерево, то имеет место неравенство
- [math]\displaystyle{ tw(G) \leq pw(G). }[/math]
Древесная ширина (и соответственно путевая ширина) графа [math]\displaystyle{ G }[/math] связана с кликовым числом [math]\displaystyle{ \omega(G) }[/math] наименьшего хордального (соответственно интервального) графа, в который рассматриваемый граф [math]\displaystyle{ G }[/math] может быть вложен, следующим образом:
- [math]\displaystyle{ tw(G) = \min \{\omega(H)| \; H\mbox{ есть хордальный граф и } G \subseteq H\} - 1 }[/math];
- [math]\displaystyle{ pw(G) = \min \{\omega(H)| \; H\mbox{ есть интервальный граф и } G \subseteq H\} - 1 }[/math].
Графы с древесной шириной [math]\displaystyle{ k }[/math] известны также как частичные [math]\displaystyle{ k }[/math]-деревья.
Ключевые слова и синонимы
Частичное k-дерево; размерность; k-разложимые графы
Постановка задачи
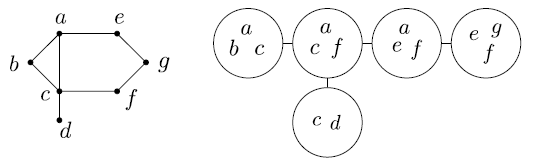
Пример. Граф и его древесная декомпозиция ширины 2
Альтернативное определение древесной ширины дается в терминах хордальных графов. Граф G = (V, E) является хордальным в том и столько том случае, если любой цикл длиной не менее 4 содержит хорду, т.е. дугу между двумя непоследовательными вершинами цикла. Древесная ширина графа G не превышает значения k в том и только том случае, если G является подграфом хордального графа H, имеющего максимальную клику размером не более k.
Также можно дать еще одно определение в терминах упорядочения вершин. Пусть [math]\displaystyle{ \pi \; }[/math] – перестановка (в данном контексте называемая схемой исключения) вершин G = (V, E). Повторить следующий шаг для i = 1, ..., |V|: взять вершину [math]\displaystyle{ \pi (i) \; }[/math], превратить множество ее соседей в клику, а затем исключить v. Ширина [math]\displaystyle{ \pi \; }[/math] равна максимуму по всем вершинам той же степени после ее исключения. Древесная ширина G равна минимальной ширине по всем схемам исключения.
Входными данными задачи нахождения древесной ширины являются неориентированный граф G = (V, E), предположительно представленный в виде списка смежности, и целое положительное число k < |V|. Необходимо определить, верно ли, что древесная ширина графа G не превышает k, и в случае положительного ответа предложить древесную декомпозицию G с шириной не более k.
Основные результаты
Теорема 1 (Арнборг и др. [1]). Пусть даны граф G и целое число k. Задача определения того факта, что древесная ширина графа G не превышает k, является недетерминированной и имеет полиномиальное время выполнения (является NP-полной).
Во многих вариантах применения древесной ширины и древесной декомпозиции графа исключительно важен случай, когда k предполагается фиксированной константой. Арнборг и др. [1] в 1987 году предложили алгоритм решения этой задачи за время [math]\displaystyle{ O(n^{k+2}) \; }[/math]. Было разработано несколько более быстрых алгоритмов для решения задачи при фиксированном значении k; обзор этих алгоритмов см, например, в [6].
Теорема 2 (Бодлендер [4]). Для каждого фиксированного значения k существует алгоритм, который для заданного графа G = (V, E) и целочисленного k может определить, верно ли, что древесная ширина G не превышает k, и в случае положительного ответа предложить древесную декомпозицию G с шириной не более k за время O(n).
Теорема 2 имеет только теоретическую значимость: на практике этот алгоритм работает слишком медленно из-за большого константного коэффициента, скрытого в O-нотации. В случае древесной ширины, равной 1, задача эквивалентна задаче распознавания деревьев. Для случаев древесной ширины 2 и 3 были предложены эффективные алгоритмы, основанные на небольшом множестве правил редукции [2].
Для поиска древесной ширины часто используются две эвристики – минимального заполнения и минимальной степени. При применении эвристики минимальной степени выбирается вершина v с минимальной степенью. Граф G' строится в результате превращения окрестности вершины v в клику и последующего удаления вершины v и инцидентных ей дуг. Хордальный суперграф H' графа G' вычисляется рекурсивным образом при помощи эвристики. Затем строится хордальный суперграф H графа G в результате добавления вершины v и инцидентных ей дуг из G в H'. Эвристика минимального заполнения работает сходным образом, однако в данном случае выбирается такая вершина v, чтобы количество ребер, добавляемых для превращения ее окрестности в клику, было минимально возможным.
Теорема 3 (Фомин и др. [9]). Существует алгоритм, который для данного графа G = (V, E) определяет его древесную ширину и находит его древесную декомпозицию минимальной ширины за время [math]\displaystyle{ O(1,8899^n) \; }[/math].
Бушитте и Тодинка [8] показали, что древесная ширина может быть вычислена за полиномиальное время для графов, имеющих полиномиальное число минимальных сепараторов. На этой основе были разработаны алгоритмы с полиномиальным временем выполнения для нескольких классов графов – таких как перестановочные графы или слабо триангулированные графы.
Применение
Один из основных способов применения понятий древесной ширины и древесной декомпозиции заключается в следующем: многие задачи, трудноразрешимые (например, NP-полные) в случае произвольных графов, становятся разрешимыми за полиномиальное или линейное время в случае графов с ограниченной древесной шириной. К числу задач, для которых может быть применена эта техника, относятся многие классические графовые и сетевые задачи – такие как нахождение гамильтонова контура, дерева Штейнера, вершинного покрытия, независимого множества и раскраски графа – однако она может применяться и к множеству других задач. Она также используется алгоритмом, разработанным Лауритценом и Шпигельхальтером [11], для решения задачи логического вывода на вероятностных сетях (байесовых или «сетях доверия»). Подобные алгоритмы обычно имеют следующий вид. Вначале вычисляется древесная декомпозиция ограниченной ширины, а затем выполняется динамический алгоритм, использующий эту древесную декомпозицию. Нередко время выполнения динамического алгоритма оказывается экспоненциальным относительно ширины используемой древесной декомпозиции, в силу чего ее желательно выбирать насколько возможно малой.
Также известны общие характеристики классов задач, разрешимых за линейное время на графах с ограниченной древесной шириной. Наиболее важным является класс задач, которые можно сформулировать в терминах монадической логики второго порядка и ее расширений.
Древесная ширина использовалась в контексте нескольких приложений или теоретических исследований, включая теорию миноров графов, базы данных, удовлетворение ограничений, распределение частот, компиляторную оптимизацию и электрические сети.
Открытые вопросы
Существуют алгоритмы нахождения древесной ширины с полиномиальным временем выполнения, гарантирующие нахождение ширины [math]\displaystyle{ O(k \sqrt{log \; k}) }[/math] для графов с древесной шириной k, однако остается открытым вопрос, существует ли алгоритм аппроксимации для нахождения древесной ширины за полиномиальное время с постоянным качественным коэффициентом. Еще один давний вопрос заключается в том, существует ли алгоритм вычисления древесной ширины с полиномиальным временем выполнения для планарных графов.
Также не решена задача разработки алгоритма для случая, когда граница древесной ширины графа k фиксирована – такого, чтобы время выполнения алгоритма как функция от n было полиномиальным, а как функция от k было значительно лучше, чем у алгоритма из теоремы 2.
Основание степени для экспоненциального времени выполнения алгоритма из теоремы 3, вероятно, может быть улучшено.
Экспериментальные результаты
Были предложены и экспериментально протестированы различные алгоритмы вычисления древесной ширины (эвристики нахождения верхней границы, эвристики нахождения нижней границы, точные алгоритмы и методы предварительной обработки). Обзор результатов многих подобных проверок приведен в работе [7]. Вариант алгоритма Арнборга и др. [1] внедрили Шойхет и Гейгер [15]. Рориг [14] провел экспериментальную оценку алгоритма Бодлендера с линейным временем выполнения [4] и установил, что он оказывается непрактичным даже для малых значений k. Часто используются эвристики минимальной степени и минимального заполнения [10].
Наборы данных
Набор тестовых графов и результаты применения многих алгоритмов на этих графах можно найти в библиотеке TreewidthLIB [16].
См. также
Литература
1. Arnborg, S., Corneil, D.G., Proskurowski, A.: Complexity of finding embeddings in a k-tree. SIAM J. Algebr. Discret. Methods 8, 277-284(1987)
2. Arnborg, S., Proskurowski, A.: Characterization and recognition of partial 3-trees. SIAM J. Algebr. Discret. Methods 7, 305-314 (1986)
3. Bodlaender, H.L.: A tourist guide through treewidth. Acta Cybernetica 11,1-23 (1993)
4. Bodlaender, H.L.: A linear time algorithm for finding tree-decompositions of small treewidth. SIAM J. Comput. 25, 1305-1317(1996)
5. Bodlaender, H.L.: A partial k-arboretum of graphs with bounded treewidth. Theor. Comp. Sci. 209,1-45 (1998)
6. Bodlaender, H.L.: Discovering treewidth. In: P. Vojtas, M. Bielikova, B. Charron-Bost (eds.) Proceedings 31st Conference on Current Trends in Theory and Practive of Computer Science, SOFSEM 2005. Lecture Notes in Computer Science, vol. 3381, pp. 1-16. Springer, Berlin (2005)
7. Bodlaender, H.L.: Treewidth: Characterizations, applications, and computations. In: Fomin, F.V. (ed.) Proceedings 32nd International Workshop on Graph-Theoretic Concepts in Computer Science WG'06. Lecture Notes in Computer Science, vol. 4271, pp. 1-14. Springer, Berlin (2006)
8. Bouchitte, V., Todinca, I.: Listing all potential maximal cliques of a graph. Theor. Comput. Sci. 276,17-32 (2002)
9. Fomin, F.V., Kratsch, D., Todinca, I., Villanger, I.: Exact (exponential) algorithms for treewidth and minimum fill-in (2006). To appear in SIAM Journal of Computing, Preliminary version appeared in ICALP 2004
10. Koster, A.M.C.A., Bodlaender, H.L., van Hoesel, S.P.M.: Treewidth: Computational experiments. In: Broersma, H., Faigle, U., Hurink, J., Pickl, S. (eds.) Electronic Notes in Discrete Mathematics, vol. 8, pp. 54-57. Elsevier, Amsterdam (2001)
11. Lauritzen, S.J., Spiegelhalter, D.J.: Local computations with probabilities on graphical structures and their application to expert systems. J. Royal Stat. Soc. Ser. B (Methodological) 50, 157-224(1988)
12. Reed, B.A.: Tree width and tangles, a new measure of connectivity and some applications, LMS Lecture Note Series, vol. 241, pp. 87-162. Cambridge University Press, Cambridge (1997)
13. Reed, B.A.: Algorithmic aspects of tree width, pp. 85-107. CMS Books Math. Ouvrages Math. SMC, 11. Springer, New York (2003)
14. Rohrig, H.: Tree decomposition: A feasibility study. Master's thesis, Max-Planck-Institut fur Informatik, SaarbrCicken, Germany (1998)
15. Shoikhet, K., Geiger, D.: A practical algorithm for finding optimal triangulations. In: Proc. National Conference on Artificial Intelligence (AAAI '97), pp. 185-190. Morgan Kaufmann, San Fransisco(1997)
16. Bodlaender, H.L.: Treewidthlib. http://www.cs.uu.nl/people/hansb/treewidthlib (2004)
Литература
- Workshop. Herrsching, 1994 // Lect. Notes Comp. Sci., 1995, vol. 903.