Сходство между сжатыми строками
Ключевые слова и синонимы
Приближенное сравнение сжатых строк; выравнивание сжатых строк
Постановка задачи
Задача вычисления сходства между двумя строками заключается в сравнении двух строк с помощью некоторой метрики оценки. Существуют различные метрики оценки; одной из самых популярных является метрика расстояния Левенштейна (или расстояния редактирования). Стандартное решение для метрики расстояния Левенштейна, предложенное Вагнером и Фишером [13], основано на динамическом программировании. Также широко используются такие метрики оценки, как метрика самой длинной общей подпоследовательности, метрика взвешенного расстояния редактирования и метрика аффинного штрафа за гэп (пропуск в последовательности). Последняя имеет наиболее общий характер и является довольно сложной для применения. В таблице 1 показаны различия между этими четырьмя метриками.
| Метрика | Совпадение | Несовпадение | Indel-расстояние | Indel-расстояние для k символов |
|---|---|---|---|---|
| Самая длинная общая подпоследовательность | 1 | 0 | 0 | 0 |
| Расстояние Левенштейна | 0 | 1 | 1 | [math]\displaystyle{ k }[/math] |
| Взвешенное расстояние редактирования | 0 | [math]\displaystyle{ \delta }[/math] | [math]\displaystyle{ \mu }[/math] | [math]\displaystyle{ k \mu }[/math] |
| Аффинный штраф за гэп | 1 | [math]\displaystyle{ - \delta }[/math] | [math]\displaystyle{ -\gamma - \mu }[/math] | [math]\displaystyle{ -\gamma - k \mu }[/math] |
Таблица 1. Различные метрики оценки
Далее будет рассматриваться задача поиска сходства между двумя сжатыми строками. Она связана с эффективным вычислением сходства без декомпрессии двух строк. В литературе рассматривалось решение этой задачи для случаев сжатия методом кодирования длин серий (run-length encoding) и сжатия Лемпеля-Зива (LZ) [14].
Кодирование длин серий
Строка S кодируется по длине серии, если она описывается упорядоченной последовательностью пар [math]\displaystyle{ (\sigma, i) }[/math], часто обозначаемых как [math]\displaystyle{ \sigma^i }[/math], каждая из которых состоит из символа алфавита, [math]\displaystyle{ \sigma }[/math], и целого числа, [math]\displaystyle{ i }[/math]. Каждая пара соответствует длине серии в S, состоящей из i последовательных вхождений [math]\displaystyle{ \sigma }[/math]. Например, строка aaabbbbbaccccbb может быть закодирована в виде [math]\displaystyle{ a^3 b^4 a^1 c^4 b^2 }[/math] или, что эквивалентно, (a, 3) (b, 4) (a, 1) (c, 4) (b, 2). Пусть A и B – две строки длиной n и m, соответственно, A' и B' – закодированные при помощи длин серий строки A и B, а n' и m' – длины строк A' и B', соответственно.
Задача 1
Дано: две строки A' и B', закодированные при помощи длин серий; метрика оценки d.
Требуется: найти сходство между A' и B' с использованием метрики d.
Сжатие Лемпеля-Зива (LZ-компрессия)
Пусть X и Y – две строки длиной O(n); X' и Y' – сжатые алгоритмом LZ строки X и Y, соответственно. Тогда длины X' и Y' равны O(hn/log n), где [math]\displaystyle{ h \le 1 }[/math] – энтропия строк X и Y.
Задача 2
Дано: две LZ-сжатые строки X' и Y', метрика оценки d.
Требуется: найти сходство между X' и Y' с использованием метрики d.
Блочное вычисление
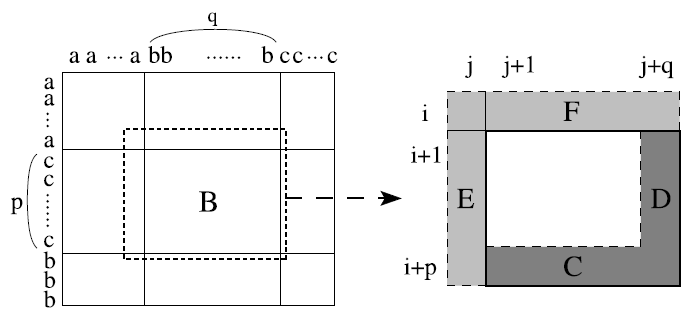
Для эффективного вычисления сходства между сжатыми строками можно использовать метод блочного вычисления. Таблицы динамического программирования делятся на подматрицы, называемые блоками. Для строк с кодированием длин серий блок представляет собой подматрицу, состоящую из двух элементов – серий по A и серий по B. Для строк с LZ-сжатием блоком является подматрица, состоящая из двух фраз – по одной фразе из каждой строки. Подробнее об этом см. в [5]. Затем блоки вычисляются слева направо и сверху вниз. Для каждого блока вычисляются только нижняя строка и крайний правый столбец. Пример вычисления блоков приведен на рис. 1.
Рисунок 1. Таблица динамического программирования для строк [math]\displaystyle{ a^r c^p b^t }[/math] и [math]\displaystyle{ a^s b^q c^u }[/math], разбитая на 9 блоков. Для одного из блоков, например, B, из E и F вычисляются только нижняя строка C и крайний правый столбец D
Основные результаты
Задача вычисления сходства двух строк A' и B', закодированных длинами серий, была изучена для различных метрик оценки. Бунке и Цирик [4] первыми предложили решение задачи 1, используя метрику самой длинной общей подпоследовательности. Их алгоритм основан на блочном вычислении таблицы динамического программирования.
Теорема 1 (Бунке и Цирик, 1995 [4]). Самая длинная общая подпоследовательность строк A' и B', закодированных длинами серий, может быть вычислена за время O(nm' + n'm).
Для метрики расстояния Левенштейна Арбелл, Ландау и Митчелл [2] и Мякинен, Наварро и Укконен [10] независимо друг от друга представили алгоритмы с временем выполнения O(nm' + n'm). Эти алгоритмы являются расширениями алгоритма Бунке и Цирика.
Теорема 2 (Арбелл, Ландау и Митчелл, 2002 [2]; Мякинен, Наварро и Укконен [10]). Расстояние Левенштейна между строками A' и B', закодированными длинами серий, может быть вычислено за время O(nm' + n'm).
Для метрики взвешенного расстояния редактирования Крочмор, Ландау и Зив-Укельсон [6] и Мякинен, Наварро и Укконен [11] предложили алгоритмы с временем выполнения O(nm' + n'm), используя совершенно отличные друг от друга методы. Алгоритм Крочмора, Ландау и Зив-Укельсона [6] основывается на технике, которая используется в алгоритме сравнения с шаблоном для текста с LZ-сжатием [6], тогда как алгоритм Мякинена, Наварро и Укконена [11] является расширением алгоритма для метрики расстояния Левенштейна.
Теорема 3 (Крочмор, Ландау и Зив-Укельсон, 2003 [6]; Мякинен, Наварро и Укконен [11]). Взвешенное расстояние редактирования между строками A' и B', закодированными длинами серий, может быть вычислено за время O(nm' + n'm).
Для метрики аффинного штрафа за гэп Ким, Амир, Ландау и Парк [8] предложили алгоритм с временем выполнения O(nm' + n'm). Для эффективного вычисления сходства в этой метрике задача преобразуется в задачу поиска пути в ориентированном ациклическом графе, и при ее решении используются некоторые свойства максимальных путей в этом графе. Нет необходимости строить граф в явном виде, так как авторы предложили новые рекуррентности, использующие свойства графа.
Теорема 4 (Ким, Амир, Ландау и Парк, 2005 [8]). Сходство между закодированными длинами серий строками A' и B' согласно метрике аффинного штрафа за гэп может быть вычислено за время O(nm' + n'm).
Приведенные выше результаты показывают, что сравнение закодированных длинами серий строк с использованием метрики самой длинной общей подпоследовательности успешно распространяется на метрики оценки более общего плана.
Для метрики самой длинной общей подпоследовательности существуют более эффективные алгоритмы. Апостолико, Ландау и Скиена [1] предложили алгоритм с временем выполнения O(n' m' log(n' m')), основанный на отслеживании конкретных оптимальных путей.
Теорема 5 (Апостолико, Ландау и Скиена, 1999 [1]). Самая длинная общая подпоследовательность строк A' и B', закодированных длинами серий, может быть вычислена за время O(n' m' log(n' + m')).
Митчелл [12] получил алгоритм с временем выполнения O((d + n' + m') log(d + n' + m')), где d – число совпадений сжатых символов. Этот алгоритм основан на вычислении геометрических кратчайших путей с помощью специальных выпуклых функций расстояния.
Теорема 6 (Митчелл, 1997 [12]). Самая длинная общая подпоследовательность строк A' и B', закодированных длинами серий, может быть вычислена за время O((d + n' + m') log(d + n' + m')), где d – число совпадений сжатых символов.
Мякинен, Наварро и Укконен [11] пришли к выводу, что среднее время работы алгоритма составляет O(n'm') в предположении, что распределение длин серий одинаково в обеих строках.
Гипотеза 1 (Мякинен, Наварро и Укконен, 2003 [11]). Самая длинная подпоследовательность строк A' и B', закодированных длинами серий, в среднем может быть вычислена за время O(n'm').
Для задачи 2 Крочмор, Ландау и Зив-Укельсон [6] представили решение с использованием метрики аддитивного штрафа за гэп. Метрика аддитивного штрафа за гэп состоит из трех элементов: 1 – для совпадения, [math]\displaystyle{ - \delta }[/math] для несовпадения и [math]\displaystyle{ - \mu }[/math] для indel (вставки и удаления), что практически совпадает с метрикой взвешенного расстояния редактирования.
Теорема 7 (Крочмор, Ландау и Зив-Укельсон, 1993 [6]). Сходство между LZ-сжатыми строками X' и Y' в метрике аддитивного штрафа за гэп может быть вычислено за время [math]\displaystyle{ O(h n^2 / log \; n) }[/math], где [math]\displaystyle{ h \le 1 }[/math] – энтропия строк X и Y.
Применение
Кодирование длин серий является популярным методом сжатия изображений, поскольку многие классы изображений (например, двоичные изображения при факсимильной передаче или при использовании в оптическом распознавании символов) обычно содержат большие участки пикселей с одинаковыми значениями. Нахождение приближенного соответствия в изображениях может быть полезным инструментом для работы с искажениями. Даже одномерный алгоритм приближенного сравнения для сжатого текста был бы полезен для ускорения двумерного приближенного сравнения, допускающего несовпадения и даже повороты [3, 7, 9].
Открытые вопросы
Сложность задачи в наихудшем случае не вполне понятна. Для метрики самой длинной общей подпоследовательности найдены некоторые результаты с временной сложностью оптимальнее O(nm' + n'm) при вычислении сходства двух строк, закодированных при помощи длин серий [1, 11, 12]. Остается открытым вопрос о распространении этих результатов на метрику расстояния Левенштейна, метрику взвешенного расстояния редактирования и метрику аффинного штрафа за гэп.
Кроме того, для метрики самой длинной общей подпоследовательности не решена задача доказательства гипотезы 1.
См. также
- Сравнение с шаблоном для сжатого текста
- Локальное выравнивание (с аффинными штрафами за гэп)
- Последовательное приближенное сравнение строк
Литература
1. Apostolico, A., Landau, G.M., Skiena, S.: Matching for Run-Length Encoded Strings. J. Complex. 15(1), 4-16 (1999)
2. Arbell, O., Landau, G.M., Mitchell, J.: Edit Distance of Run-Length Encoded Strings. Inf. Proc. Lett. 83(6), 307-314 (2002)
3. Baeza-Yates, R., Navaro, G.: New Models and Algorithms for Multidimensional Approximate Pattern Matching. J. Discret. Algorithms 1(1), 21^9 (2000)
4. Bunke, H., Csirik, H.: An Improved Algorithm for Computing the Edit Distance of Run Length Coded Strings. Inf. Proc. Lett. 54, 93-96(1995)
5. Crochemore, M., Landau, G.M., Schieber, B., Ziv-Ukelson, M.: Re-Use Dynamic Programming for Sequence Alignment: An Algorithmic Toolkit. In: Iliopoulos, C.S., Lecroq, T. (eds.) String Algorithmics, pp. 19-59. King's College London Publications, London (2005)
6. Crochemore, M., Landau, G.M.,Ziv-Ukelson, M.: A Subquadratic Sequence Alignment Algorithm for Unrestricted Scoring Matrices. SIAM J. Comput. 32(6), 1654-1673 (2003)
7. Fredriksson, K., Navarro, G., Ukkonen, E.: Sequential and Indexed Two-Dimensional Combinatorial Template Matching Allowing Rotations. Theor. Comput. Sci. 347(1-2), 239-275 (2005)
8. Kim, J.W., Amir, A., Landau, G.M., Park, K.: Computing Similarity of Run-Length Encoded Strings with Affine Gap Penalty. In: Proc. 12th Symposium on String Processing and Information Retrieval (SPIRE'05). LNCS, vol. 3772, pp. 440-449 (2005)
9. Krithivasan, K., Sitalakshmi, R.: Efficient Two-Dimensional Pattern Matching in The Presence of Errors. Inf. Sci. 43, 169-184 (1987)
10. Makinen, V., Navarro, G., Ukkonen, E.: Approximate Matching of Run-Length Compressed Strings. In: Proc. 12th Symposium on Combinatorial Pattern Matching (CPM'01). LNCS, vol. 2089, pp. 31-49 (2001)
11. Makinen, V., Navarro, G., Ukkonen, E.: Approximate Matching of Run-Length Compressed Strings. Algorithmica 35, 347-369 (2003)
12. Mitchell, J.: A Geometric Shortest Path Problem, with Application to Computing a Longest Common Subsequence in Run-Length Encoded Strings. Technical Report, Dept. of Applied Mathematics, SUNY Stony Brook (1997)
13. Wagner, R.A., Fischer, M.J.: The String-to-String correction Problem. J.ACM 21(1), 168-173(1974)
14. Ziv, J., Lempel, A.: Compression of Individual Sequences via Variable Rate Coding. IEEE Trans. Inf. Theory 24(5), 530-536 (1978)