Супердерево максимального соответствия

Постановка задачи

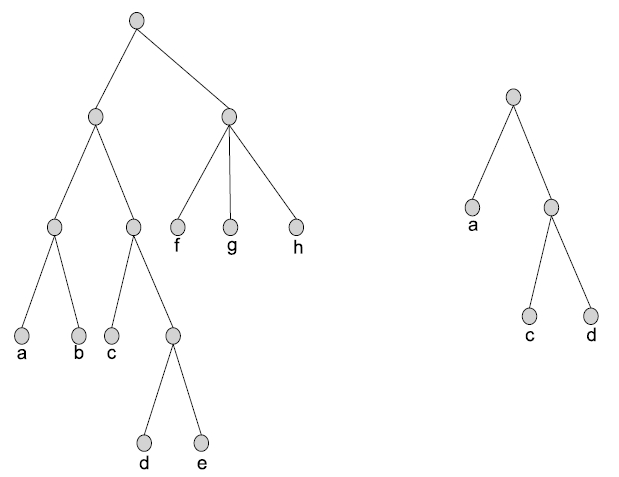
Пусть T – дерево, листья которого уникальным образом снабжены метками из набора таксонов S. Под уникальным образом мы понимаем то обстоятельство, что в T нет двух листьев с одинаковыми метками. Если дано подмножество S' множества S, то топологическое ограничение T согласно S' (обозначается T|S') представляет собой дерево, полученное в результате удаления из T всех вершин, не лежащих ни на одном пути из корня к листу из подмножества S', вместе с инцидентными им ребрами, и последующего сжатия каждого ребра между вершиной, имеющей только одного потомка, и самим этим потомком (см. рисунок). Для любого дерева T обозначим множество меток его листьев как [math]\displaystyle{ \Lambda (T) \; }[/math].

Пусть T – исходное дерево с левой стороны. Тогда дерево справа T|{a, c, d} – это топологическое ограничение дерева T.

Задача нахождения супердерева максимального соответствия (maximum agreement supertree problem, MASP) [8] определяется следующим образом.

Задача 1. Пусть [math]\displaystyle{ D = \{ T_1, T_2, ..., T_k \} \; }[/math] – множество корневых неупорядоченных деревьев, в котором каждое дерево [math]\displaystyle{ T_i \; }[/math] имеет уникальные метки листьев, при этом множества меток листьев [math]\displaystyle{ \Lambda (T_i) \; }[/math] могут перекрываться. Задача нахождения супердерева максимального соответствия заключается в построении дерева [math]\displaystyle{ Q \; }[/math] с уникальными метками листьев, с множеством меток листьев [math]\displaystyle{ \Lambda (Q) \subseteq \bigcup_{T_i \in D} \Lambda (T_i) \; }[/math], таким, что [math]\displaystyle{ | \Lambda (Q) | \; }[/math] максимально и для каждого [math]\displaystyle{ T_i \in D \; }[/math] топологическое ограничение [math]\displaystyle{ T_i \; }[/math] согласно [math]\displaystyle{ \Lambda (Q) \; }[/math] изоморфно топологическому ограничению [math]\displaystyle{ Q \; }[/math] согласно [math]\displaystyle{ \Lambda (T_i) \; }[/math].

Далее будут использоваться следующие обозначения: [math]\displaystyle{ n = | \bigcup_{T_i \in D} \Lambda (T_i) | \; }[/math], [math]\displaystyle{ k = | D | \; }[/math] и [math]\displaystyle{ D = max_{T_i \in D} \big\{ deg(T_i) \big\} \; }[/math], где [math]\displaystyle{ deg(T_i) \; }[/math] – степень [math]\displaystyle{ T_i \; }[/math].

Основные результаты

Лемма устанавливает отношение между задачами нахождения супердерева максимального соответствия и поддерева максимального соответствия.

Лемма 1 ([8]). Для любого множества [math]\displaystyle{ D = \{ T_1, T_2, ..., T_k \} \; }[/math] корневых неупорядоченных деревьев с уникальными метками листьев, таких, что [math]\displaystyle{ \Lambda(T_1) = \Lambda(T_2) = ... = \Lambda(T_k) \; }[/math], оптимальное решение задачи MASP для D является оптимальным решением задачи MAST для D, и наоборот.

Из леммы следует теорема 2, описывающая время вычисления супердерева максимального соответствия для двух деревьев.

Теорема 2. ([8]) Если k = 2 (имеются два дерева), супердерево максимального соответствия может быть найдено за время [math]\displaystyle{ O(T_{MAST} + n) \; }[/math], где [math]\displaystyle{ T_{MAST} \; }[/math] – время, необходимое для вычисления поддерева максимального соответствия двух деревьев с O(n) листьями. Заметим, что [math]\displaystyle{ T_{MAST} = O( \sqrt{Dn} \; log(2n/D)) \; }[/math] (см. [9]).

В [11] было приведено обобщение теоремы 2 и предложено следующее решение.

Теорема 3 ([1]). Для любого фиксированного k > 2 в случае, если каждый лист D встречается в 1 дереве либо в k деревьев, супердерево максимального соответствия может быть найдено за время [math]\displaystyle{ O(T'_{MAST} + kn) \; }[/math], где [math]\displaystyle{ T'_{MAST} \; }[/math] – время, необходимое для вычисления поддерева максимального соответствия k деревьев с метками листьев из [math]\displaystyle{ \bigcap_{T_i \in D} \Lambda(T_i) \; }[/math]. Заметим, что [math]\displaystyle{ T'_{MAST} = O(km^3 + m^D) \; }[/math], где [math]\displaystyle{ n = | \bigcap_{T_i \in D} \Lambda(T_i) | \; }[/math] (см. [4]).

Следующие две теоремы доказывают, что в общем случае задача вычисления супердерева максимального соответствия является NP-полной.

Теорема 4 ([8, 1]). Для любого фиксированного [math]\displaystyle{ k \ge 3 \; }[/math] задача MASP с неограниченной величиной D является NP-полной. Более того, задача MASP является NP-полной даже в случае, когда мы ограничиваемся корневыми триплетами. (Корневой триплет – это бинарное корневое неупорядоченное дерево с уникальными метками листьев, имеющее три листа).

Теорема 5 ([1]). Задача MASP не может быть приближенно решена за полиномиальное время с константным множителем, если только не верно соотношение [math]\displaystyle{ \mathcal{P} = \mathcal{N} \mathcal{P} }[/math].

Хотя задача MASP является NP-полной, существует аппроксимационный алгоритм для ее приближенного решения.

Теорема 6 ([8]). Задача MASP может быть приближенно решена с множителем [math]\displaystyle{ \frac{n}{log \; n} }[/math] за время [math]\displaystyle{ O(n^2) \cdot min \{ O(k \cdot (log \; log \; n)^2), O(k + log \; n \cdot log \; log \; n) \} }[/math]. MASP, ограниченная корневыми триплетами, может быть приближенно решена с множителем [math]\displaystyle{ \frac{n}{log \; n} }[/math] за время [math]\displaystyle{ O(k + n^2 log^2 \; n) }[/math].

Также существуют алгоритмы вычисления MASP с фиксированными параметрами и полиномиальным временем решения. Случай с множеством k бинарных деревьев T с n различных меток листьев рассматривался множеством исследователей. Дженссон и коллеги [8] первыми предложили алгоритм вычисления MAST на T с временем исполнения [math]\displaystyle{ O(k(2n^2)^{3k^2}) \; }[/math]. Недавно Гийемо и Берри [5] улучшили это время до [math]\displaystyle{ O((8n)^k) \; }[/math]; Хоанг и Сунг [7] снизили его до [math]\displaystyle{ O((6n)^k) \; }[/math], что показано в теореме 7.

Теорема 7 ([7]). Пусть дано множество k бинарных деревьев T с n различных меток листьев; их супердерево максимального соответствия может быть найдено за время [math]\displaystyle{ O((6n)^k) \; }[/math].

Для случая, когда множество k бинарных деревьев T имеют степень D и n различных меток листьев, Хоанг и Сунг [7] предложили следующее решение для нахождения MASP с фиксированными параметрами и полиномиальным временем исполнения.

Теорема 8 ([7]). Пусть дано множество k бинарных деревьев T степени D с n различных меток листьев; их супердерево максимального соответствия может быть найдено за время [math]\displaystyle{ O((kD)^{kD+3} (2n)^k) \; }[/math].

Применение

Важной задачей филогенетики является разработка хороших методов слияния наборов филогенетических деревьев на перекрывающихся множествах таксонов в единое супердерево таким образом, чтобы был потерян минимально возможный (желательно – нулевой) объем информации о ветвлении. В идеале полученное супердерево может в дальнейшем использоваться для вывода эволюционных взаимоотношений между таксонами, не содержавшихся ни в одном из исходных деревьев. Методы исследований с использованием супердеревьев имеют практическую пользу, поскольку большинство отдельных исследований изучают не очень большое число таксонов [11], а также в силу того, что из-за смещения выборки некоторые таксоны исследуются намного чаще других [2]. Кроме того, методы формирования супердеревьев способны объединять деревья, построенные для различных типов данных или согласно различным моделям эволюции. Далее, хотя методы построения надежных филогенетических деревьев, требующие очень большого объема вычислений, непригодны для работы с большими наборами таксонов, они могут применяться для получения высокоточных деревьев для небольших перекрывающихся подмножеств таксонов, которые впоследствии могут быть слиты вместе при помощи менее «тяжеловесных» техник на основе супердеревьев (см., например, [3, 6, 10]).

Поскольку множества деревьев, требующих объединения, могут содержать противоречивую структуру ветвления (например, если они были построены из данных, происходящих от различных генов, либо в случае, если экспериментальные данные содержат ошибки), метод построения супердерева должен обозначить, как разрешить подобные конфликты. Интуитивно понятная идея заключается в том, чтобы определить и удалить наименьшее возможное подмножество таксонов таким образом, чтобы оставшиеся таксоны можно было объединить без каких-либо конфликтов. При использовании этого подхода нужно получить уведомление о том, какие отношения наследования можно считать беспроблемными и какие таксоны следует предложить для дальнейшего изучения. Вышеупомянутая биологическая задача может быть формализована в виде вычислительной задачи нахождения супердерева максимального соответствия (MASP).

С ней связана задача нахождения супердерева максимальной совместимости (maximum compatible supertree problem, MCSP) [ ], которая определяется следующим образом.

Задача 2. Пусть [math]\displaystyle{ D = \{ T_1, T_2, ..., T_k \} \; }[/math] – множество корневых неупорядоченных деревьев, в котором каждое дерево [math]\displaystyle{ T_i \; }[/math] имеет уникальные метки листьев, при этом множества меток листьев [math]\displaystyle{ \Lambda(T_i) \; }[/math] могут перекрываться. Задача нахождения супердерева максимальной совместимости (MCSP) заключается в построении дерева [math]\displaystyle{ Q \; }[/math] с уникальными метками листьев, с множеством меток листьев [math]\displaystyle{ \Lambda(Q) \subseteq \bigcup_{T_i \in D} \Lambda(T_i) \; }[/math], таким, что [math]\displaystyle{ | \Lambda(Q) | \; }[/math] максимально и для каждого [math]\displaystyle{ T_i \in D \; }[/math] топологическое ограничение поддерева [math]\displaystyle{ Q_i' \; }[/math] дерева [math]\displaystyle{ Q \; }[/math] согласно [math]\displaystyle{ \Lambda(T_i) \; }[/math] уточняет топологическое ограничение [math]\displaystyle{ T'_i \; }[/math] согласно [math]\displaystyle{ T_i \; }[/math]; иначе говоря, [math]\displaystyle{ T'_i \; }[/math] может быть получено путем коллапсирования определенных ребер [math]\displaystyle{ Q'_i \; }[/math].

Открытые вопросы

Существующие алгоритмы вычисления MASP с фиксированными параметрами и полиномиальным временем решения непрактичны. Важно найти эвристические подходы или улучшить время выполнения имеющихся алгоритмов.

См. также

• Поддерево максимального соответствия (для двух бинарных деревьев)
• Поддерево максимального соответствия (для трех или более деревьев)
• Дерево максимальной совместимости

Литература

1. Berry, V., Nicolas, F.: Maximum agreement and compatible supertrees. J. Discret. Algorithms (2006)

2. Bininda-Emonds, O., Gittleman, J., Steel, M.: The (super)tree of life: Procedures, problems, and prospects. Ann. Rev. Ecol. System. 33, 265-289 (2002)

3. Chor, B., Hendy, M., Penny, D.: Analytic solutions for three-taxon MLMC trees with variable rates across sites. In: Proceedings of the 1st Workshop on Algorithms in Bioinformatics (WABI 2001). Lecture Notes in Computer Science, vol. 2149, pp. 204-213. Springer (2001)

4. Farach, M., Przytycka, T., Thorup, M.: On the agreement of many trees. Information Process. Lett. 55,297-301 (1995)

5. Guillemot, S., Berry, V.: Fixed-parameter tractability of the maximum agreement supertrees. In: Proceedings of the 18th Annual Symposium on Combinatorial Pattern Matching (CPM 2007). Lecture Notes in Computer Science. Springer, (2007)

6. Henzinger, M.R., King, V., Warnow, T.: Constructing a tree from homeomorphic subtrees, with applications to computational evolutionary biology. Algorithmica 24(1), 1 -13 (1999)

7. Hoang, V.T., Sung, W.K.: Fixed Parameter Polynomial Time Algorithms for Maximum Agreement and Compatible Supertrees. In: Albers, S., Weil, P., 25th International Symposium on Theoretical Aspects of Computer Science (STACS 2008). Dagstuhl, Germany (2007)

8. Jansson, J., Joseph, H., Ng, K., Sadakane, K., Sung, W.-K.: Rooted maximum agreement supertrees. Algorithmica 43(4), 293-307 (2005)

9. Kao, M.-Y., Lam, T.-W., Sung, W.-K., Ting, H.-F.: An even faster and more unifying algorithm for comparing trees via unbalanced bipartite matchings.J.Algorithms 40(2),212-233 (2001)

10. Kearney, P.: Phylogenetics and the quartet method. In: Jiang, T., Xu, Y., Zhang, M.Q. (eds.) Current Topics in Computational Molecular Biology. The MIT Press, Massachusetts, pp. 111 -133 (2002)

11. Sanderson, M.J., Purvis, A., Henze, C.: Phylogenetic supertrees: assembling the trees of life. TRENDS in Ecology & Evolution, 13(3),105-109(1998)