Прямолинейное дерево Штейнера: различия между версиями
Irina (обсуждение | вклад) мНет описания правки |
Irina (обсуждение | вклад) мНет описания правки |
||
| (не показано 17 промежуточных версий этого же участника) | |||
| Строка 7: | Строка 7: | ||
В силу высокой значимости этой задачи для ее решения было разработано немало алгоритмов, которые можно разбить на два класса: точные и эвристические. Поскольку задача SMT является NP-полной, любой точный алгоритм будет иметь ожидаемое экспоненциальное время | В силу высокой значимости этой задачи для ее решения было разработано немало алгоритмов, которые можно разбить на два класса: точные и эвристические. Поскольку задача SMT является NP-полной, любой точный алгоритм будет иметь ожидаемое экспоненциальное время выполнения в наихудшем случае. Однако в этой области были достигнуты два значительных улучшения. Одним из них стал алгоритм GeoSteiner в реализации Уорма, Уинтера и Захарисена [14, 15] – самый быстрый на данный момент точный алгоритм для решения этой задачи. Второй алгоритм, аппроксимационная схема с полиномиальным временем выполнения (Polynomial Time Approximation Scheme, PTAS) Ароры [1], имеет скорее теоретическую значимость. Поскольку время выполнения точных алгоритмов получается очень долгим, особенно для входных данных большого объема, намного больше внимания было уделено разработке эвристических алгоритмов. Многие из них генерируют дерево Штейнера посредством улучшения топологии [[минимальное остовное дерево|минимального остовного дерева]] (MST) [7], так как было доказано, что MST является 3/2-аппроксимацией SMT [8]. Однако из-за того, что в этих подходах базовые структуры ограничены топологией минимального остовного дерева, степень улучшений по сравнению с ним ограничена. Итерационный алгоритм 1-Steiner Канга и Робинса [10] был одной из первых попыток обойти это ограничение, а его улучшенная реализация [6] стала самой популярной из подобных программ общедоступного класса. Время выполнения этого алгоритма в версии [10] составляет <math>O(n^4 \; log \; n)</math>, а реализации в [6] – <math>O(n^3) \;</math>. Намного более эффективный алгоритм позднее предложили Бора и коллеги [2]. В их версии остовное дерево итеративно улучшается за счет подключения точки к ребру и последующего удаления самого длинного ребра в получившейся схеме. Время выполнения этого алгоритма в наихудшем случае составляет <math>\Theta(n^2) \;</math>, также была предложена альтернативная реализация с временем <math>O(n \; log \; n)</math>. Поскольку базовые структуры теперь уже не ограничены топологией МОД, эффективность данного подхода сравнялась с эффективностью итеративного алгоритма 1-Steiner [2]. Недавно был предложен новый эвристический алгоритм Мандуи и др. [11], основанный на 3/2-аппроксимации алгоритма вычисления метрического дерева Штейнера на квази-двудольных графах [12]. Он работает несколько лучше итеративного алгоритма 1-Steiner, но слегка уступает этому же алгоритму в случае использования последним проверки на пустые прямоугольники [11]. Недавно Чу [3], а также Чу и Вонг [4] предложили эффективный подход на базе таблицы поиска для построения прямолинейного дерева Штейнера. | ||
== Основные результаты == | == Основные результаты == | ||
Представленный алгоритм основан на эвристике подстановки ребер, предложенной Борой и коллегами [2] и работающей следующим образом. Эвристика начинает работу с имеющегося минимального остовного дерева и итеративно рассматривает возможность подключения точки ( | Представленный алгоритм основан на эвристике подстановки ребер, предложенной Борой и коллегами [2] и работающей следующим образом. Эвристика начинает работу с имеющегося минимального остовного дерева и итеративно рассматривает возможность подключения точки (например, p на рис. 1) к ближайшему ребру (например, (a, b)) и удаления самого длинного ребра (b, c)) из получившейся схемы. Алгоритм использует [[остовный граф]] [17] как базовую структуру вычисления: вначале он используется для генерации исходного минимального остовного дерева, а затем – пар «точка-ребро» для улучшения этого дерева. Подобная унификация наблюдается также при вычислении остовного дерева и самого длиного ребра для каждой пары «точка-ребро»: эти два вычисления объединяет использование алгоритма Крускала для операций на непересекающихся множествах [5] вместо алгоритма Прима. | ||
| Строка 19: | Строка 18: | ||
Для сокращения количества потенциальных пар «точка-ребро» с O( | Для сокращения количества потенциальных пар «точка-ребро» с <math>O(n^2) \;</math> до <math>O(n) \;</math> Бора и коллеги предложили использовать параметр видимости точки со стороны ребра: только точка, видимая от ребра, может рассматриваться для подключения к нему. Для поиска отношений видимости между точками и ребрами необходим заметающий алгоритм. Чтобы избежать выполнения этого сложного этапа, используется информация о геометрической близости, встроенная в остовный граф. Поскольку у точки имеется восемь ближайших точек, подключенных вблизи нее, то можно заметить: если точка видима от ребра, то она обычно подключена в графе по меньшей мере к одной из конечных точек ребра. Алгоритм использует остовный граф для генерации пар-кандидатов «точка-ребро». Для каждого ребра текущего дерева все точки, являющиеся соседями одной из конечных точек ребра, будут рассматриваться в качестве потенциальных кандидатов на подключение к ребру. Поскольку мощность остовного графа составляет O(n), количество возможных пар, сгенерированных таким образом, также укладывается в эту оценку. | ||
При подключении точки к ребру самое длинное ребро получившейся схемы необходимо удалить. Для эффективного поиска соответствующего самого длиного ребра для каждой пары «точка-ребро» используется подход к вычислению остовного дерева при помощи алгоритма Крускала. Этот алгоритм сортирует ребра в порядке неубывания длины и рассматривает поочередно каждое ребро. Если конечные точки ребра были соединены, оно исключается из остовного дерева; в противном случае ребро включается в остовное дерево. Структура операций подключения может быть представлена бинарным деревом, листьями которого являются точки, а внутренними вершинами – ребра. После включения ребра в остовное дерево создается вершина, представляющая ребро, а также два ее потомка, представляющие два компонента, соединенные этим ребром. Пример остовного дерева и представляющего его бинарного дерева приведен на рис. 2. Легко увидеть, что самое длинное ребро между двумя точками является наименьшим общим предком этих двух точек в бинарном дереве. Например, самое длинное ребро между точками p и b на рис. 2 – ребро (b, c), наименьший общий предок p и b в бинарном дереве. Чтобы найти самое длинное ребро в схеме, образованной подключением точки к ребру, необходимо найти самое длинное ребро между этой точкой и той из конечных точек ребра, с которой она находилась в одном компоненте до подключения к ребру. Например, рассмотрим | При подключении точки к ребру самое длинное ребро получившейся схемы необходимо удалить. Для эффективного поиска соответствующего самого длиного ребра для каждой пары «точка-ребро» используется подход к вычислению остовного дерева при помощи алгоритма Крускала. Этот алгоритм сортирует ребра в порядке неубывания длины и рассматривает поочередно каждое ребро. Если конечные точки ребра были соединены, оно исключается из остовного дерева; в противном случае ребро включается в остовное дерево. Структура операций подключения может быть представлена бинарным деревом, листьями которого являются точки, а внутренними вершинами – ребра. После включения ребра в остовное дерево создается вершина, представляющая ребро, а также два ее потомка-дерева, представляющие два компонента, соединенные этим ребром. Пример остовного дерева и представляющего его бинарного дерева приведен на рис. 2. Легко увидеть, что самое длинное ребро между двумя точками является наименьшим общим предком этих двух точек в бинарном дереве. Например, самое длинное ребро между точками p и b на рис. 2 – ребро (b, c), наименьший общий предок p и b в бинарном дереве. Чтобы найти самое длинное ребро в схеме, образованной подключением точки к ребру, необходимо найти самое длинное ребро между этой точкой и той из конечных точек ребра, с которой она находилась в одном компоненте до подключения к ребру. Например, рассмотрим пару из точки p и ребра (a, b). Поскольку p и b принадлежали к одному компоненту до подключения (a, b), самым длинным ребром оказывается ребро между p и b; его и нужно удалить. | ||
| Строка 30: | Строка 29: | ||
На основе вышеприведенных рассуждений создан псевдокод алгоритма, представленный на рис. 3. На начальном этапе работы алгоритма для генерации остовного графа G для заданного множества точек используется алгоритм построения прямолинейного остовного графа Чжоу и др [17]. Затем к графу применяется алгоритм Крускала для генерации минимального остовного дерева. Структура данных на основе непересекающихся множеств [ ] используется для слияния компонентов и проверки, принадлежат ли две точки к одному и тому же компоненту (первый цикл for). В процессе выполнения также генерируются бинарное дерево слияния и запросы по поводу наименьших общих предков для всех пар «точка-ребро». Здесь s, s1 и s2 представляют непересекающиеся множества, каждое из которых хранит корень компонента в бинарном дереве слияния. При каждом добавлении дуги (u, v) к T следует рассматривать любого соседа u или v, обозначим его за w, как кандидата на подключение к (u, v). Самое длиное ребро для этой пары будет наименьшим общим предком w и u либо w и v, в зависимости от того, какая точка оказывается в одном компоненте с точкой w. Добавление этого опроса производится при помощи процедуры lca_add_query. Соединение двух компонентов | На основе вышеприведенных рассуждений создан псевдокод алгоритма, представленный на рис. 3. На начальном этапе работы алгоритма для генерации остовного графа G для заданного множества точек используется алгоритм построения прямолинейного остовного графа Чжоу и др [17]. Затем к графу применяется алгоритм Крускала для генерации минимального остовного дерева. Структура данных на основе непересекающихся множеств [5] используется для слияния компонентов и проверки, принадлежат ли две точки к одному и тому же компоненту (первый цикл '''for'''). В процессе выполнения также генерируются бинарное дерево слияния и запросы по поводу наименьших общих предков для всех пар «точка-ребро». Здесь s, s1 и s2 представляют непересекающиеся множества, каждое из которых хранит корень компонента в бинарном дереве слияния. При каждом добавлении дуги (u, v) к T следует рассматривать любого соседа u или v, обозначим его за w, как кандидата на подключение к (u, v). Самое длиное ребро для этой пары будет наименьшим общим предком w и u либо w и v, в зависимости от того, какая точка оказывается в одном компоненте с точкой w. Добавление этого опроса производится при помощи процедуры lca_add_query. Соединение двух компонентов посредством (u, v) также будет записано в бинарном дереве слияния при помощи процедуры lca_tree_edge. После генерации минимального остовного дерева у нас также имеются соответствующее бинарное дерево слияния и запросы по поводу наименьших общих предков. При помощи оффлайнового алгоритма Тарьяна для нахождения наименьших общих предков [5] (представленного процедурой lca_answer_queries) можно сгенерировать все самые длинные ребра для пар. При наличии информации о самом длинном ребре для каждой пары «точка-ребро» можно решить задачу подключения точки к ребру. После этого можно осуществить подключения точек к ребрам в порядке невозрастания прироста. Подключение может быть осуществлено только в случае, если ни ребро подключения, ни ребро удаления еще не были удалены. | ||
Большую часть времени | Большую часть времени выполнения алгоритма занимают генерация остовного графа и сортировка ребер, требующие O(n log n) времени. Поскольку количество ребер в остовном графе составляет O(n), и алгоритм Крускала, и алгоритм Тарьяна для поиска наименьших общих предков занимают <math>O(n \alpha (n)) \;</math> времени, где <math>\alpha (n) \;</math> – обратная функция Аккермана, растущая исключительно медленно. | ||
| Строка 40: | Строка 39: | ||
'''for''' (каждой дуги <math>(u, v) \in G \;</math> по порядку неубывания длины) { | '''for''' (каждой дуги <math>(u, v) \in G \;</math> по порядку неубывания длины) { | ||
s1 = find_set(u); s2 = find_set(v); | s1 = find_set(u); s2 = find_set(v); | ||
'''if''' (s1!=s2){ | '''if''' (s1 != s2) { | ||
добавить (u, v) в дерево T; | добавить (u, v) в дерево T; | ||
'''for''' (каждого соседа w точек u, v в G) | '''for''' (каждого соседа w точек u, v в G) | ||
| Строка 51: | Строка 50: | ||
} | } | ||
} | } | ||
сгенерировать пары «точка-ребро» | сгенерировать пары «точка-ребро» при помощи lca_answer_queries; | ||
'''for''' (каждой пары (p, (a, b), (c, d)) в порядке невозрастания положительного прироста) | '''for''' (каждой пары (p, (a, b), (c, d)) в порядке невозрастания положительного прироста) | ||
'''if''' (ребро (a, b), (c ,d) не было удалено из T) { | '''if''' (ребро (a, b), (c ,d) не было удалено из T) { | ||
| Строка 59: | Строка 58: | ||
Рисунок 3. Алгоритм построения прямолинейного дерева Штейнера. | Рисунок 3. Алгоритм построения прямолинейного дерева Штейнера. | ||
== Применение == | == Применение == | ||
| Строка 66: | Строка 64: | ||
== Экспериментальные результаты == | == Экспериментальные результаты == | ||
Как отмечалось в работе [16], первая серия экспериментов была проведена на Linux-системе с процессором Intel Pentium III с тактовой частотой | Как отмечалось в работе [16], первая серия экспериментов была проведена на Linux-системе с процессором Intel Pentium III с тактовой частотой 928 МГц и 512 Мбайт оперативной памяти. Алгоритм RST сравнивался с другими публично доступными программами: точным алгоритмом GeoSteiner (версии 3.1) Уорма, Уинтера и Захарисена [14], пакетным итеративным алгоритмом 1-Steiner (Batched Iterated 1-Steiner, BI1S) Робинса и алгоритмом Боры и коллег, реализованным Мэдденом (BOI). | ||
В таблице 1 приведены результаты первой серии экспериментов. Для каждого экземпляра входных данных объемом от 100 до 5000 точек при помощи программы rand_points пакета GeoSteiner было случайно сгенерировано 30 различных тестовых сценариев. Коэффициент улучшения алгоритма вычисления дерева Штейнера St по сравнению с соответствующим алгоритмом вычисления минимального остовного дерева MST определяется как 100 x (MST - St)/MST. Для каждого варианта объема входных данных были вычислены средние значения коэффициента улучшения и времени | В таблице 1 приведены результаты первой серии экспериментов. Для каждого экземпляра входных данных объемом от 100 до 5000 точек при помощи программы rand_points пакета GeoSteiner было случайно сгенерировано 30 различных тестовых сценариев. Коэффициент улучшения алгоритма вычисления дерева Штейнера St по сравнению с соответствующим алгоритмом вычисления минимального остовного дерева MST определяется как 100 x (MST - St)/MST. Для каждого варианта объема входных данных были вычислены средние значения коэффициента улучшения и времени выполнения (в секундах) каждой из программ. Легко увидеть, что RST всегда обеспечивает более высокую эффективность по сравнению с BOI при меньшей продолжительности работы. | ||
Во второй серии экспериментов сравнивались алгоритмы RST, версия Боры его собственного алгоритма (Borah), алгоритм Роэ на базе подхода Прима (Rohe) [13] и жадный пакетный алгоритм Канга и др. (Batched Greedy Algorithm, BGA) [9]. Они | Во второй серии экспериментов сравнивались алгоритмы RST, версия Боры его собственного алгоритма (Borah), алгоритм Роэ на базе подхода Прима (Rohe) [13] и жадный пакетный алгоритм Канга и др. (Batched Greedy Algorithm, BGA) [9]. Они выполнялись на различных Linux-системах с процессором Intel Xeon с 2,4 ГГц тактовой частоты и 2 ГБ оперативной памяти. Помимо случайно сгенерированных тестовых сценариев, также использовались промышленные тестовые сценарии из области разработки СБИС [9]. Результаты представлены в таблице 2. | ||
{| class = "wikitable" | {| class = "wikitable" | ||
| Строка 79: | Строка 77: | ||
! colspan="2" width="200" | BI1S | ! colspan="2" width="200" | BI1S | ||
! colspan="2" width="200" | BOI | ! colspan="2" width="200" | BOI | ||
! colspan="2" width="200" | | ! colspan="2" width="200" | RST | ||
|- | |- | ||
! | улучш. | ! | улучш. | ||
| Строка 92: | Строка 90: | ||
| 100||11,440||0,487||10,907||0,633||9,300||0,0267||10,218||0,004 | | 100||11,440||0,487||10,907||0,633||9,300||0,0267||10,218||0,004 | ||
|- | |- | ||
| 200||11,492|3,557||10,897||4,810||9,192||0,1287||10,869||0,020 | | 200||11,492||3,557||10,897||4,810||9,192||0,1287||10,869||0,020 | ||
|- | |- | ||
| 300||11,492||12,685||10,931||18,770||9,253||0,2993||10,255||0,041 | | 300||11,492||12,685||10,931||18,770||9,253||0,2993||10,255||0,041 | ||
| Строка 117: | Строка 115: | ||
! colspan="2" width="200" | BI1S | ! colspan="2" width="200" | BI1S | ||
! colspan="2" width="200" | BOI | ! colspan="2" width="200" | BOI | ||
! colspan="2" width="200" | | ! colspan="2" width="200" | RST | ||
|- | |- | ||
! | улучш. | ! | улучш. | ||
Текущая версия от 14:32, 1 октября 2023
Ключевые слова и синонимы
Метрическое минимальное дерево Штейнера; кратчайшее дерево маршрутизации
Постановка задачи
Пусть даны точки на плоскости. Минимальное дерево Штейнера (SMT) соединяет эти точки при помощи дополнительных точек, называемых точками Штейнера, так, чтобы общая сумма расстояний между ними была минимальной. Если в качестве расстояния между двумя точками берется расстояние по прямой, такое дерево называется прямолинейным минимальным деревом Штейнера.
В силу высокой значимости этой задачи для ее решения было разработано немало алгоритмов, которые можно разбить на два класса: точные и эвристические. Поскольку задача SMT является NP-полной, любой точный алгоритм будет иметь ожидаемое экспоненциальное время выполнения в наихудшем случае. Однако в этой области были достигнуты два значительных улучшения. Одним из них стал алгоритм GeoSteiner в реализации Уорма, Уинтера и Захарисена [14, 15] – самый быстрый на данный момент точный алгоритм для решения этой задачи. Второй алгоритм, аппроксимационная схема с полиномиальным временем выполнения (Polynomial Time Approximation Scheme, PTAS) Ароры [1], имеет скорее теоретическую значимость. Поскольку время выполнения точных алгоритмов получается очень долгим, особенно для входных данных большого объема, намного больше внимания было уделено разработке эвристических алгоритмов. Многие из них генерируют дерево Штейнера посредством улучшения топологии минимального остовного дерева (MST) [7], так как было доказано, что MST является 3/2-аппроксимацией SMT [8]. Однако из-за того, что в этих подходах базовые структуры ограничены топологией минимального остовного дерева, степень улучшений по сравнению с ним ограничена. Итерационный алгоритм 1-Steiner Канга и Робинса [10] был одной из первых попыток обойти это ограничение, а его улучшенная реализация [6] стала самой популярной из подобных программ общедоступного класса. Время выполнения этого алгоритма в версии [10] составляет [math]\displaystyle{ O(n^4 \; log \; n) }[/math], а реализации в [6] – [math]\displaystyle{ O(n^3) \; }[/math]. Намного более эффективный алгоритм позднее предложили Бора и коллеги [2]. В их версии остовное дерево итеративно улучшается за счет подключения точки к ребру и последующего удаления самого длинного ребра в получившейся схеме. Время выполнения этого алгоритма в наихудшем случае составляет [math]\displaystyle{ \Theta(n^2) \; }[/math], также была предложена альтернативная реализация с временем [math]\displaystyle{ O(n \; log \; n) }[/math]. Поскольку базовые структуры теперь уже не ограничены топологией МОД, эффективность данного подхода сравнялась с эффективностью итеративного алгоритма 1-Steiner [2]. Недавно был предложен новый эвристический алгоритм Мандуи и др. [11], основанный на 3/2-аппроксимации алгоритма вычисления метрического дерева Штейнера на квази-двудольных графах [12]. Он работает несколько лучше итеративного алгоритма 1-Steiner, но слегка уступает этому же алгоритму в случае использования последним проверки на пустые прямоугольники [11]. Недавно Чу [3], а также Чу и Вонг [4] предложили эффективный подход на базе таблицы поиска для построения прямолинейного дерева Штейнера.
Основные результаты
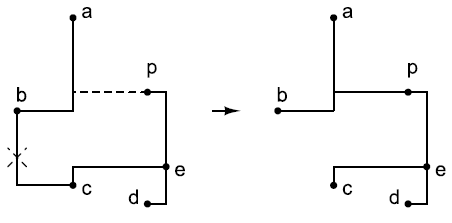
Представленный алгоритм основан на эвристике подстановки ребер, предложенной Борой и коллегами [2] и работающей следующим образом. Эвристика начинает работу с имеющегося минимального остовного дерева и итеративно рассматривает возможность подключения точки (например, p на рис. 1) к ближайшему ребру (например, (a, b)) и удаления самого длинного ребра (b, c)) из получившейся схемы. Алгоритм использует остовный граф [17] как базовую структуру вычисления: вначале он используется для генерации исходного минимального остовного дерева, а затем – пар «точка-ребро» для улучшения этого дерева. Подобная унификация наблюдается также при вычислении остовного дерева и самого длиного ребра для каждой пары «точка-ребро»: эти два вычисления объединяет использование алгоритма Крускала для операций на непересекающихся множествах [5] вместо алгоритма Прима.
Рисунок 1. Подстановка ребра в алгоритме Боры и др.
Для сокращения количества потенциальных пар «точка-ребро» с [math]\displaystyle{ O(n^2) \; }[/math] до [math]\displaystyle{ O(n) \; }[/math] Бора и коллеги предложили использовать параметр видимости точки со стороны ребра: только точка, видимая от ребра, может рассматриваться для подключения к нему. Для поиска отношений видимости между точками и ребрами необходим заметающий алгоритм. Чтобы избежать выполнения этого сложного этапа, используется информация о геометрической близости, встроенная в остовный граф. Поскольку у точки имеется восемь ближайших точек, подключенных вблизи нее, то можно заметить: если точка видима от ребра, то она обычно подключена в графе по меньшей мере к одной из конечных точек ребра. Алгоритм использует остовный граф для генерации пар-кандидатов «точка-ребро». Для каждого ребра текущего дерева все точки, являющиеся соседями одной из конечных точек ребра, будут рассматриваться в качестве потенциальных кандидатов на подключение к ребру. Поскольку мощность остовного графа составляет O(n), количество возможных пар, сгенерированных таким образом, также укладывается в эту оценку.
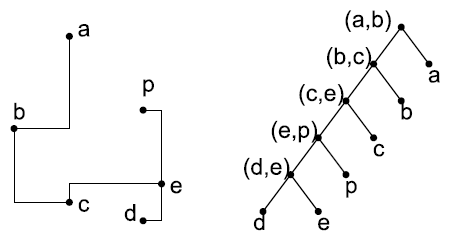
При подключении точки к ребру самое длинное ребро получившейся схемы необходимо удалить. Для эффективного поиска соответствующего самого длиного ребра для каждой пары «точка-ребро» используется подход к вычислению остовного дерева при помощи алгоритма Крускала. Этот алгоритм сортирует ребра в порядке неубывания длины и рассматривает поочередно каждое ребро. Если конечные точки ребра были соединены, оно исключается из остовного дерева; в противном случае ребро включается в остовное дерево. Структура операций подключения может быть представлена бинарным деревом, листьями которого являются точки, а внутренними вершинами – ребра. После включения ребра в остовное дерево создается вершина, представляющая ребро, а также два ее потомка-дерева, представляющие два компонента, соединенные этим ребром. Пример остовного дерева и представляющего его бинарного дерева приведен на рис. 2. Легко увидеть, что самое длинное ребро между двумя точками является наименьшим общим предком этих двух точек в бинарном дереве. Например, самое длинное ребро между точками p и b на рис. 2 – ребро (b, c), наименьший общий предок p и b в бинарном дереве. Чтобы найти самое длинное ребро в схеме, образованной подключением точки к ребру, необходимо найти самое длинное ребро между этой точкой и той из конечных точек ребра, с которой она находилась в одном компоненте до подключения к ребру. Например, рассмотрим пару из точки p и ребра (a, b). Поскольку p и b принадлежали к одному компоненту до подключения (a, b), самым длинным ребром оказывается ребро между p и b; его и нужно удалить.
Рисунок 2. Минимальное остовное дерево и его бинарное дерево слияния.
На основе вышеприведенных рассуждений создан псевдокод алгоритма, представленный на рис. 3. На начальном этапе работы алгоритма для генерации остовного графа G для заданного множества точек используется алгоритм построения прямолинейного остовного графа Чжоу и др [17]. Затем к графу применяется алгоритм Крускала для генерации минимального остовного дерева. Структура данных на основе непересекающихся множеств [5] используется для слияния компонентов и проверки, принадлежат ли две точки к одному и тому же компоненту (первый цикл for). В процессе выполнения также генерируются бинарное дерево слияния и запросы по поводу наименьших общих предков для всех пар «точка-ребро». Здесь s, s1 и s2 представляют непересекающиеся множества, каждое из которых хранит корень компонента в бинарном дереве слияния. При каждом добавлении дуги (u, v) к T следует рассматривать любого соседа u или v, обозначим его за w, как кандидата на подключение к (u, v). Самое длиное ребро для этой пары будет наименьшим общим предком w и u либо w и v, в зависимости от того, какая точка оказывается в одном компоненте с точкой w. Добавление этого опроса производится при помощи процедуры lca_add_query. Соединение двух компонентов посредством (u, v) также будет записано в бинарном дереве слияния при помощи процедуры lca_tree_edge. После генерации минимального остовного дерева у нас также имеются соответствующее бинарное дерево слияния и запросы по поводу наименьших общих предков. При помощи оффлайнового алгоритма Тарьяна для нахождения наименьших общих предков [5] (представленного процедурой lca_answer_queries) можно сгенерировать все самые длинные ребра для пар. При наличии информации о самом длинном ребре для каждой пары «точка-ребро» можно решить задачу подключения точки к ребру. После этого можно осуществить подключения точек к ребрам в порядке невозрастания прироста. Подключение может быть осуществлено только в случае, если ни ребро подключения, ни ребро удаления еще не были удалены.
Большую часть времени выполнения алгоритма занимают генерация остовного графа и сортировка ребер, требующие O(n log n) времени. Поскольку количество ребер в остовном графе составляет O(n), и алгоритм Крускала, и алгоритм Тарьяна для поиска наименьших общих предков занимают [math]\displaystyle{ O(n \alpha (n)) \; }[/math] времени, где [math]\displaystyle{ \alpha (n) \; }[/math] – обратная функция Аккермана, растущая исключительно медленно.
[math]\displaystyle{ T = \empty }[/math]; Сгенерировать остовный граф G при помощи алгоритма RSG; for (каждой дуги [math]\displaystyle{ (u, v) \in G \; }[/math] по порядку неубывания длины) { s1 = find_set(u); s2 = find_set(v); if (s1 != s2) { добавить (u, v) в дерево T; for (каждого соседа w точек u, v в G) if (s1 == find_set(w)) lca_add_query(w, u, (u, v)); else lca_add_query(w, v, (u, v)); lca_tree_edge((u, v), s1.edge); lca_tree_edge((u, v), s2.edge); s = union_set(s1, s2); s.edge = (u, v); } } сгенерировать пары «точка-ребро» при помощи lca_answer_queries; for (каждой пары (p, (a, b), (c, d)) в порядке невозрастания положительного прироста) if (ребро (a, b), (c ,d) не было удалено из T) { подключить p к (a, b), добавив три ребра к T; удалить (a, b), (c, d) из T; }
Рисунок 3. Алгоритм построения прямолинейного дерева Штейнера.
Применение
Алгоритм построения минимального дерева Штейнера (SMT) широко применяется в САПР для проектирования СБИС. Он обычно используется при создании инициальной топологии некритических сетей в процессе физического синтеза. Для критических по времени сетей минимизации длины кабелей обычно бывает недостаточно. Однако, поскольку большинство сетей являются некритическими в проектировании и алгоритм SMT дает наиболее желаемый маршрут для подобных сетей, он часто используется в качестве точной оценки нагруженности и длины кабелей в процессе планирования на плоскости и размещения. В силу этого алгоритм построения дерева Штейнера будет вызываться миллионы раз. С другой стороны, при разработке современных СБИС применяются различные варианты предварительной разводки. Эти варианты обычно моделируются в виде больших множеств точек, из-за чего объем входных данных для задачи построения дерева Штейнера повышается. Поскольку эта задача будет вычисляться миллионы раз и во многих случаях на очень больших объемах входных данных, для ее вычисления нужны очень эффективные решения.
Экспериментальные результаты
Как отмечалось в работе [16], первая серия экспериментов была проведена на Linux-системе с процессором Intel Pentium III с тактовой частотой 928 МГц и 512 Мбайт оперативной памяти. Алгоритм RST сравнивался с другими публично доступными программами: точным алгоритмом GeoSteiner (версии 3.1) Уорма, Уинтера и Захарисена [14], пакетным итеративным алгоритмом 1-Steiner (Batched Iterated 1-Steiner, BI1S) Робинса и алгоритмом Боры и коллег, реализованным Мэдденом (BOI).
В таблице 1 приведены результаты первой серии экспериментов. Для каждого экземпляра входных данных объемом от 100 до 5000 точек при помощи программы rand_points пакета GeoSteiner было случайно сгенерировано 30 различных тестовых сценариев. Коэффициент улучшения алгоритма вычисления дерева Штейнера St по сравнению с соответствующим алгоритмом вычисления минимального остовного дерева MST определяется как 100 x (MST - St)/MST. Для каждого варианта объема входных данных были вычислены средние значения коэффициента улучшения и времени выполнения (в секундах) каждой из программ. Легко увидеть, что RST всегда обеспечивает более высокую эффективность по сравнению с BOI при меньшей продолжительности работы.
Во второй серии экспериментов сравнивались алгоритмы RST, версия Боры его собственного алгоритма (Borah), алгоритм Роэ на базе подхода Прима (Rohe) [13] и жадный пакетный алгоритм Канга и др. (Batched Greedy Algorithm, BGA) [9]. Они выполнялись на различных Linux-системах с процессором Intel Xeon с 2,4 ГГц тактовой частоты и 2 ГБ оперативной памяти. Помимо случайно сгенерированных тестовых сценариев, также использовались промышленные тестовые сценарии из области разработки СБИС [9]. Результаты представлены в таблице 2.
| Входные данные | GeoSteiner | BI1S | BOI | RST | ||||
|---|---|---|---|---|---|---|---|---|
| улучш. | время | улучш. | время | улучш. | время | улучш. | время | |
| 100 | 11,440 | 0,487 | 10,907 | 0,633 | 9,300 | 0,0267 | 10,218 | 0,004 |
| 200 | 11,492 | 3,557 | 10,897 | 4,810 | 9,192 | 0,1287 | 10,869 | 0,020 |
| 300 | 11,492 | 12,685 | 10,931 | 18,770 | 9,253 | 0,2993 | 10,255 | 0,041 |
| 500 | 11,525 | 72,192 | - | - | 9,274 | 0,877 | 10,381 | 0,084 |
| 800 | 11,343 | 536,173 | - | - | 9,284 | 2,399 | 10,719 | 0,156 |
| 1000 | - | - | - | - | 9,367 | 4,084 | 10,433 | 0,186 |
| 2000 | - | - | - | - | 9,326 | 31,098 | 10,523 | 0,381 |
| 3000 | - | - | - | - | 9,390 | 104,919 | 10,449 | 0,771 |
| 5000 | - | - | - | - | 9,356 | 307,977 | 10,499 | 1,330 |
Таблица 1. Сравнение с другими алгоритмами (первая серия).
| Входные данные | GeoSteiner | BI1S | BOI | RST | ||||
|---|---|---|---|---|---|---|---|---|
| улучш. | время | улучш. | время | улучш. | время | улучш. | время | |
| Случайно сгенерированные тестовые сценарии | ||||||||
| 100 | 10,272 | 0,006 | 10,341 | 0,004 | 9,617 | 0,000 | 10,218 | 0,002 |
| 500 | 10,976 | 0,068 | 10,778 | 0,178 | 10,028 | 0,010 | 10,381 | 0,041 |
| 1000 | 10,979 | 0,162 | 10,829 | 0,689 | 9,768 | 0,020 | 10,433 | 0,121 |
| 5000 | 11,012 | 1,695 | 11,015 | 25,518 | 10,139 | 0,130 | 10,499 | 0,980 |
| 10000 | 11,108 | 4,135 | 11,101 | 249,924 | 10,111 | 0,310 | 10,559 | 2,098 |
| 50000 | 11,120 | 59,147 | - | - | 10,109 | 1,890 | 10,561 | 13,029 |
| 100000 | 11,098 | 161,896 | - | - | 10,079 | 4,410 | 10,514 | 28,527 |
| 500000 | - | - | - | - | 10,059 | 27,210 | 10,527 | 175,725 |
| Тестовые сценарии из области разработки СБИС | ||||||||
| 337 | 6,434 | 0,035 | 6,503 | 0,037 | 5,958 | 0,010 | 5,870 | 0,016 |
| 830 | 3,202 | 0,070 | 3,185 | 0,213 | 3,102 | 0,020 | 2,966 | 0,033 |
| 1944 | 7,850 | 0,342 | 7,772 | 2,424 | 6,857 | 0,040 | 7,533 | 0,238 |
| 2437 | 7,965 | 0,549 | 7,956 | 4,502 | 7,094 | 0,050 | 7,595 | 0,408 |
| 2676 | 8,928 | 0,623 | 8,994 | 3,686 | 8,067 | 0,060 | 8,507 | 0,463 |
| 12052 | 8,450 | 4,289 | 8,465 | 232,779 | 7,649 | 0,300 | 8,076 | 2,281 |
| 22373 | 9,848 | 11,330 | 9,832 | 1128,365 | 8,987 | 0,570 | 9,462 | 4,605 |
| 34728 | 9,046 | 18,416 | 9,010 | 2367,629 | 8,158 | 0,900 | 8,645 | 5,334 |
Таблица 2. Сравнение с другими алгоритмами (вторая серия).
См. также
Литература
1. Arora, S.: Polynomial-time approximation schemes for euclidean tsp and other geometric problem. J. ACM 45, 753-782 (1998)
2. Borah, M., Owens, R.M., Irwin, M.J.: An edge-based heuristic for steiner routing. IEEE Transac. Comput. Aided Des. 13, 1563-1568(1994)
3. Chu, C.: FLUTE: Fast lookup table based wirelength estimation technique. In: Proc. Intl. Conf. on Computer-Aided Design, San Jose, Nov. 2004, pp. 696-701
4. Chu, C., Wong, Y.C.: Fast and accurate rectilinear steiner minimal tree algorithm for vlsi design. In: International Symposium on Physical Design, pp. 28-35 (2005)
5. Cormen, T.H., Leiserson, C.E., Rivest, R.L.: Introduction to Algorithms. MIT Press, Cambridge (1989)
6. Griffith, J., Robins, G., Salowe, J.S., Zhang, T.: Closing the gap: Near-optimal steiner trees in polynomial time. IEEE Transac. Comput. Aided Des. 13,1351-1365 (1994)
7. Ho, J.M., Vijayan, G., Wong, C.K.: New algorithms for the rectilinear steiner tree problem. IEEE Transac. Comput. Aided Des. 9,185-193(1990)
8. Hwang, F.K.: On Steiner minimal trees with rectilinear distance. SIAM J. Appl. Math. 30,104-114 (1976)
9. Kahng, A.B., Mandoiu, I.I., Zelikovsky, A.: Highly scalable algorithms for rectilinear and octilinear steiner trees. In: Proc. Asia and South Pacific Design Automation Conference, Kitakyushu, Japan, (2003) pp. 827-833
10. Kahng, A.B., Robins, G.: A new class of iterative steiner tree heuristics with good performance. IEEE Transac. Comput. Aided Des. 11,893-902 (1992)
11. Mandoiu, I.I., Vazirani, V.V., Ganley, J.L.: A new heuristic for rectilinear Steiner trees. In: Proc. Intl. Conf. on Computer-Aided Design, San Jose, (1999)
12. Rajagopalan, S., Vazirani, V.V.: On the bidirected cut relaxation for the metric Steiner tree problem. In: 10th ACM-SIAM Symposium on Discrete Algorithms, Baltimore, (1999), pp. 742-751
13. Rohe, A.: Sequential and Parallel Algorithms for Local Routing. Ph.D. thesis, Bonn University, Bonn, Germany, Dec. (2001)
14. Warme, D.M., Winter, P., Zacharisen, M.: GeoSteiner 3.1 package. ftp://ftp.diku.dk/diku/users/martinz/geosteiner-3.1.tar.gz. Accessed Oct. 2003
15. Warme, D.M., Winter, P., Zacharisen, M.: Exact algorithms for plane steiner tree problems: A computational study, Tech. Rep. DIKU-TR-98/11, Dept. of Computer Science, University of Copenhagen (1998)
16. Zhou, H.: A new efficient retiming algorithm derived by formal manipulation. In: Workshop Notes of Intl. Workshop on Logic Synthesis, Tem ecula, CA, June (2004)
17. Zhou, H., Shenoy, N., Nicholls, W.: Efficient spanning tree construction without delaunay triangulation. Inf. Process. Lett. 81, 271-276(2002)