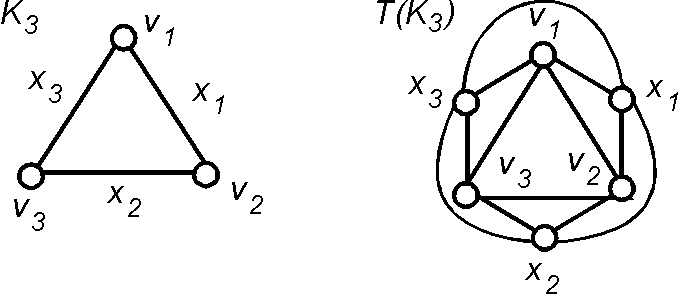Тотальный граф: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''Тотальный граф''' (''[[Total graph]]'') | '''Тотальный граф''' (''[[Total graph]]'') — | ||
для данного [[граф|графа]] <math>G</math> граф <math>T(G)</math>, у которого множеством [[вершина|вершин]] является | для данного [[граф|графа]] <math>\,G</math> граф <math>\,T(G)</math>, у которого множеством [[вершина|вершин]] является | ||
<math>V(G) \cup E(G)</math> и две вершины в <math>T(G)</math> [[смежные вершины|смежны]], если они соседние (т.е. смежные | <math>V(G) \cup E(G)</math> и две вершины в <math>\,T(G)</math> [[смежные вершины|смежны]], если они соседние (т.е. смежные | ||
или [[инцидентность|инцидентные]]) в графе <math>G</math>. | или [[инцидентность|инцидентные]]) в графе <math>\,G</math>. | ||
[[Файл:Total graph.gif|500px]] | [[Файл:Total graph.gif|500px]] | ||
==Литература== | ==Литература== | ||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
* Харари Ф. Теория графов. — М.: Мир, 1973. | |||
Текущая версия от 05:43, 20 сентября 2011
Тотальный граф (Total graph) — для данного графа [math]\displaystyle{ \,G }[/math] граф [math]\displaystyle{ \,T(G) }[/math], у которого множеством вершин является [math]\displaystyle{ V(G) \cup E(G) }[/math] и две вершины в [math]\displaystyle{ \,T(G) }[/math] смежны, если они соседние (т.е. смежные или инцидентные) в графе [math]\displaystyle{ \,G }[/math].
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.
- Харари Ф. Теория графов. — М.: Мир, 1973.