Схема с косвенной адресацией: различия между версиями
KVN (обсуждение | вклад) |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
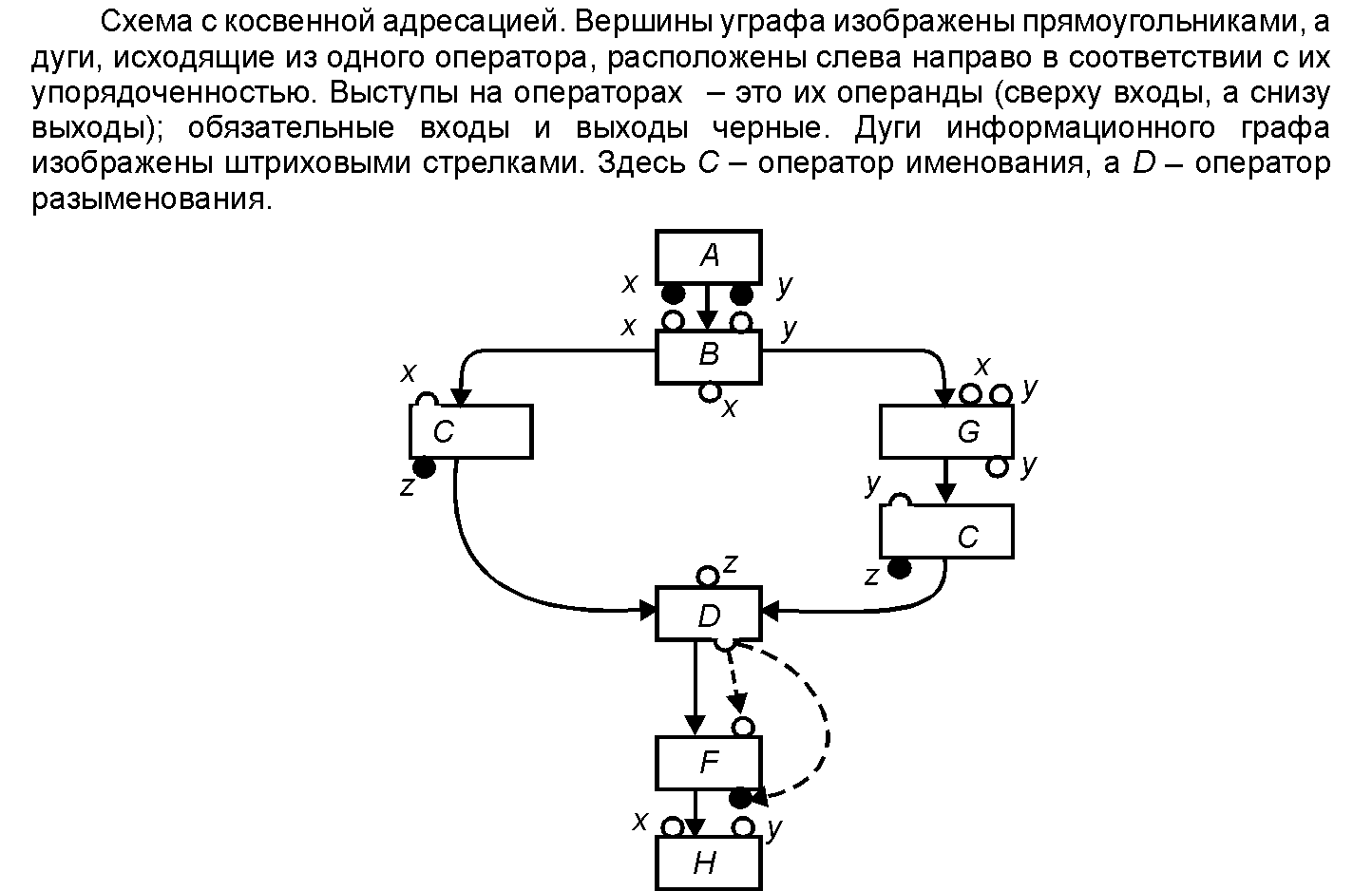
'''Схема с косвенной адресацией''' (''[[Scheme with indirect addressing]]'') | '''Схема с косвенной адресацией''' (''[[Scheme with indirect addressing]]'') — | ||
При рассмотрении среди переменных особых величин | При рассмотрении среди переменных особых величин — | ||
''указателей'', значениями которых являются имена других | ''указателей'', значениями которых являются имена других | ||
переменных (в частности, указателей), | переменных (в частности, указателей), — возникают две новые | ||
операции: ''именования'' (присваивания указателю имени | операции: ''именования'' (присваивания указателю имени | ||
переменной) и ''разыменования'' (выборки имени переменной как | переменной) и ''разыменования'' (выборки имени переменной как | ||
| Строка 10: | Строка 10: | ||
имеет одного преемника, один [[вход]] и один [[выход]]. | имеет одного преемника, один [[вход]] и один [[выход]]. | ||
Входы операторов именования и выходы операторов | Входы операторов именования и выходы операторов | ||
разыменования называются фиктивными. '''Схема с косвенной адресацией''' | разыменования называются фиктивными. '''Схема с косвенной адресацией''' — это тройка | ||
<math>(G,J,R)</math>, в которой <math>G</math> | <math>(G,J,R)</math>, в которой <math>G</math> — ''[[управляющий граф]]'', <math>J</math> — | ||
''[[информационный граф]]'', [[дуга|дуги]] которого исходят из фиктивных | ''[[информационный граф]]'', [[дуга|дуги]] которого исходят из фиктивных | ||
выходов, а <math>R</math> | выходов, а <math>R</math> — ''[[раскраска]]'', ставящая в соответствие переменные тем | ||
операндам, которые не имеют [[инцидентность|инцидентных]] дуг в <math>J</math>. | операндам, которые не имеют [[инцидентность|инцидентных]] дуг в <math>J</math>. | ||
| Строка 25: | Строка 25: | ||
Другое название | Другое название — ''[[КА-Схема]]''. | ||
==См. также == | ==См. также == | ||
''[[Крупноблочная схема программ]], [[Неинтерпретированные схемы]], [[Стандартные схемы]], [[Схема программ]], [[Схема с распределенной памятью]], [[Схемы Мартынюка]].'' | * ''[[Крупноблочная схема программ]],'' | ||
* ''[[Неинтерпретированные схемы]],'' | |||
* ''[[Стандартные схемы]],'' | |||
* ''[[Схема программ]],'' | |||
* ''[[Схема с распределенной памятью]],'' | |||
* ''[[Схемы Мартынюка]].'' | |||
==Литература== | ==Литература== | ||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
[[Категория:Теория схем программ]] | [[Категория:Теория схем программ]] | ||
Текущая версия от 04:49, 12 сентября 2011
Схема с косвенной адресацией (Scheme with indirect addressing) — При рассмотрении среди переменных особых величин — указателей, значениями которых являются имена других переменных (в частности, указателей), — возникают две новые операции: именования (присваивания указателю имени переменной) и разыменования (выборки имени переменной как значения указателя). В соответствии с этим можно рассматривать в схемах программ интерпретированные операторы именования и разыменования, каждый из которых имеет одного преемника, один вход и один выход. Входы операторов именования и выходы операторов разыменования называются фиктивными. Схема с косвенной адресацией — это тройка [math]\displaystyle{ (G,J,R) }[/math], в которой [math]\displaystyle{ G }[/math] — управляющий граф, [math]\displaystyle{ J }[/math] — информационный граф, дуги которого исходят из фиктивных выходов, а [math]\displaystyle{ R }[/math] — раскраска, ставящая в соответствие переменные тем операндам, которые не имеют инцидентных дуг в [math]\displaystyle{ J }[/math].
Основной вопрос в исследовании схемы с косвенной адресацией состоит в нахождении покрывающих множеств для аргументов и результатов операторов и информационных связей схемы.
Другое название — КА-Схема.
См. также
- Крупноблочная схема программ,
- Неинтерпретированные схемы,
- Стандартные схемы,
- Схема программ,
- Схема с распределенной памятью,
- Схемы Мартынюка.
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.