T-Нумерация: различия между версиями
Перейти к навигации
Перейти к поиску
KVN (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''T-Нумерация''' (''[[T-Numbering]]'') | '''<math>\,T</math>-Нумерация''' (''[[T-Numbering|<math>\,T</math>-Numbering]]'') — | ||
такая ''[[нумерация вершин]]'' [[уграф|уграфа]], что для некоторой фиксированной его | такая ''[[нумерация вершин]]'' [[уграф|уграфа]], что для некоторой фиксированной его | ||
''[[обратная нумерация|обратной нумерации]]'' <math>N</math> справедливы следующие свойства: | ''[[обратная нумерация|обратной нумерации]]'' <math>\,N</math> справедливы следующие свойства: | ||
(1) для любых | (1) для любых | ||
''[[бивершина|бивершин]]'' <math>p</math> и <math>q</math>: <math>T(p) < T(q)</math> тогда и только тогда, когда | ''[[бивершина|бивершин]]'' <math>\,p</math> и <math>\,q</math>: <math>\,T(p) < T(q)</math> тогда и только тогда, когда | ||
<math>N(p) < N(q)</math>; | <math>\,N(p) < N(q)</math>; | ||
(2) <math>T</math>-номера [[вершина|вершин]] [[F-Область|<math>N</math>-''области'']] <math>N[p]</math> вершины <math>p</math> | (2) <math>\,T</math>-номера [[вершина|вершин]] [[F-Область|<math>\,N</math>-''области'']] <math>\,N[p]</math> вершины <math>\,p</math> | ||
образуют отрезок <math>[T(p),T(p)+|N[p]| - 1]</math>. | образуют отрезок <math>\,[T(p),T(p)+|N[p]| - 1]</math>. | ||
[[Файл:T-Numbering.png|500px]] | [[Файл:T-Numbering.png|500px]] | ||
==Литература== | ==Литература== | ||
* Евстигнеев В. А., Касьянов В. Н. Графы в программировании: обработка, визуализация и применение. — СПб.: БХВ-Петербург, 2003. | |||
*Касьянов В. Н. | * Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | ||
Версия от 05:23, 20 мая 2011
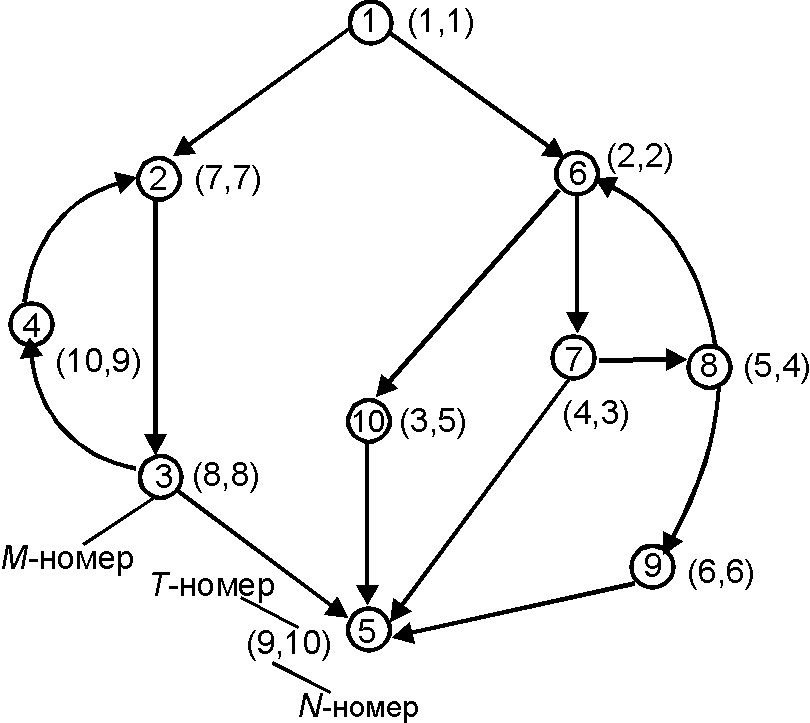
[math]\displaystyle{ \,T }[/math]-Нумерация ([math]\displaystyle{ \,T }[/math]-Numbering) — такая нумерация вершин уграфа, что для некоторой фиксированной его обратной нумерации [math]\displaystyle{ \,N }[/math] справедливы следующие свойства:
(1) для любых бивершин [math]\displaystyle{ \,p }[/math] и [math]\displaystyle{ \,q }[/math]: [math]\displaystyle{ \,T(p) \lt T(q) }[/math] тогда и только тогда, когда [math]\displaystyle{ \,N(p) \lt N(q) }[/math];
(2) [math]\displaystyle{ \,T }[/math]-номера вершин [math]\displaystyle{ \,N }[/math]-области [math]\displaystyle{ \,N[p] }[/math] вершины [math]\displaystyle{ \,p }[/math] образуют отрезок [math]\displaystyle{ \,[T(p),T(p)+|N[p]| - 1] }[/math].
Литература
- Евстигнеев В. А., Касьянов В. Н. Графы в программировании: обработка, визуализация и применение. — СПб.: БХВ-Петербург, 2003.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.