Редукция данных для доминирования в графах: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 13 промежуточных версий 1 участника) | |||
| Строка 4: | Строка 4: | ||
NP-полная задача поиска доминирующего множества (DOMINATING SET), как известно, представляет значительную сложность. | NP-полная задача поиска доминирующего множества (DOMINATING SET), как известно, представляет значительную сложность. | ||
Дано: неориентированный граф <math>G = (V, E) \; </math> и целое число <math>k \ge 0 \; </math>. | |||
Дано: неориентированный граф G = (V, E) и целое число k > | |||
Вопрос: существует ли подграф S | Вопрос: существует ли подграф <math>S \subseteq V</math> с <math>|S| \le k \; </math>, такой, что каждая вершина <math>v \in V \; </math> входит в S, либо по крайней мере один из ее соседей входит в S? | ||
К примеру, построить оптимизированную версию графа с n вершинами за полиномиальное время можно только с точностью до множителя | К примеру, построить оптимизированную версию графа с n вершинами за полиномиальное время можно только с точностью до множителя <math>\Theta (log \; n) \; </math>, если не выполняются некоторые стандартные теоретико-сложностные предположения [9]. В терминах параметризованной сложности эта задача, как было показано в [8], является W[2]-полной. Для планарных графов она по-прежнему является NP-полной, однако в данном случае ситуация оказывается намного проще. В своей основополагающей работе Бэйкер показала, что существует аппроксимационная схема с полиномиальным временем выполнения (PTAS) [6], и что в случае планарных графов эта задача становится разрешимой при помощи алгоритмов с фиксированными параметрами [2, 4]. В частности, задача может иметь решение при использовании достаточно эффективных правил редукции; может быть доказан результат кернелизации (общее описание редукции данных и кернелизации см. в [16]). | ||
== Основные результаты == | == Основные результаты == | ||
Основная идея редукции данных заключается в предварительной обработке на основе локально применяемых правил упрощения. В качестве примера может служить правило, согласно которому рассматривается локальная окрестность каждой вершины графа. Для этого потребуются следующие определения. | Основная идея редукции данных заключается в предварительной обработке на основе локально применяемых правил упрощения. В качестве примера может служить правило, согласно которому рассматривается локальная окрестность каждой вершины графа. Для этого потребуются следующие определения. | ||
Окрестность N(v) произвольной вершины v | Окрестность N(v) произвольной вершины <math>v \in V \; </math> входного графа разбивается на три непересекающихся множества <math>N_1(v) \; </math>, <math>N_2(v) \; </math> и <math>N_3(v) \; </math>, зависящих от структуры локальной окрестности. Эти множества таковы: | ||
В левой части рисунка показано подобное разбиение. Понятная и полезная интерпретация данного разбиения заключается в том, что вершины из | <math>N_1(v) \; </math> содержит всех соседей вершины v, от которых идут дуги к вершинам, не являющимся соседями v; | ||
Рассмотрим вершину w | |||
Если | <math>N_2(v) \; </math> содержит все вершины из <math>N(v) \setminus N_1(v) \; </math>, связанные дугами по крайней мере с одной вершиной из <math>N_1(v) \; </math>; | ||
<math>N_3(v) \; </math> содержит всех соседей вершины v, не принадлежащих к <math>N_1(v) \; </math> или <math>N_2(v) \; </math>. | |||
[[Файл:DRDG.jpg]] | |||
''Редукция данных для доминирования в графах'' | |||
''В левой части показано разбиение окрестности вершины v; в правой части показан результат применения приведенного ниже правила редукции данных к этому конкретному (под)графу.'' | |||
В левой части рисунка показано подобное разбиение. Понятная и полезная интерпретация данного разбиения заключается в том, что вершины из <math>N_1(v) \; </math> рассматриваются как «выходы», поскольку они имеют прямые связи с «внешним миром» за пределами ближайшей окрестности v; вершины из <math>N_2(v) \; </math> – как «стражи», поскольку они имеют прямую связь с выходами, а вершины из <math>N_3(v) \; </math> – как «заключенные», поскольку они не видят «мира» за пределами <math> \{ v \} \cup N_1(v) \; </math>. | |||
Рассмотрим вершину <math>w \in N_3(v) \; </math>. Такая вершина имеет соседей только из <math> \{ v \} \cup N_1(v) \cup N_3(v) \; </math>. Следовательно, для того, чтобы доминировать вершину w, по меньшей мере одна вершина из <math> \{ v \} \cup N_1(v) \cup N_3(v) \; </math> должна входить в доминирующее множество входного графа. Поскольку v может доминировать все вершины, которые были бы доминированы в результате выбора из <math>N_1(v) \cup N_3(v) \; </math> в доминирующее множество, это дает следующее правило редукции данных: | |||
Если <math>N_3(v) \ne \emptyset \; </math> для некоторой вершины v, удалить <math>N_2(v) \; </math> и <math>N_3(v) \; </math> из G и добавить в G новую вершину v' с дугой {v, v'}. | |||
Новая вершина v' может рассматриваться как «вершина-гаджет», которая «заставляет» выбрать v в доминирующее множество. Корректность этого правила нетрудно проверить, поскольку она сводится к тому, что исходный граф имеет доминирующее множество размера k в том и только том случае, если приведенный в результате редукции граф имеет доминирующее множество размера k. Очевидно, что редукция данных может быть проведена за полиномиальное время [5]. Однако существуют «ромбовидные» структуры, к которым данное правило редукции неприменимо. Для них было предложено несколько более сложное правило, основанное на рассмотрении объединенной окрестности двух вершин [5]. | |||
В [5] была доказана справедливость следующей теоремы. | В [5] была доказана справедливость следующей теоремы. | ||
Теорема 1. Планарный граф G = (V, E) может быть за полиномиальное время приведен при помощи редукции к планарному графу | |||
Иными словами, теорема утверждает, что задача нахождения доминирующего множества в планарных графах (DOMINATING SET) имеет ядро линейного размера. Значение верхней границы | | '''Теорема 1. Планарный граф G = (V, E) может быть за полиномиальное время приведен при помощи редукции к планарному графу G' = (V', E'), такому, что G имеет доминирующее множество размера k в том и только том случае, если G0 имеет доминирующее множество размера k и |V'| = O(k).''' | ||
Иными словами, теорема утверждает, что задача нахождения доминирующего множества в планарных графах (DOMINATING SET) имеет ядро линейного размера. Значение верхней границы |V'| вначале было установлено равным 335k [5], затем снижено до 67k [7]. Эти результаты могут быть расширены на графы ограниченного рода [10]. Кроме того, подобные же результаты (линейная кернелизация) были недавно получены для задачи нахождения полноразмерного остовного дерева в планарном графе (FULL-DEGREE SPANNING TREE) [13]. Впоследствии эти результаты были обобщены в виде методологической схемы [12]. | |||
== Применение == | == Применение == | ||
| Строка 45: | Строка 60: | ||
== Литература == | == Литература == | ||
1. Alber, J., Betzler, N., Niedermeier, R.: Experiments on data reduction for optimal domination in networks. Ann. Oper. Res. 146(1), 105–117 (2006) | 1. Alber, J., Betzler, N., Niedermeier, R.: Experiments on data reduction for optimal domination in networks. Ann. Oper. Res. 146(1), 105–117 (2006) | ||
2. Alber, J., Bodlaender, H.L., Fernau, H., Kloks, T., Niedermeier, R.: Fixed parameter algorithms for Dominating Set and related problems on planar graphs. Algorithmica 33(4), 461–493 (2002) | 2. Alber, J., Bodlaender, H.L., Fernau, H., Kloks, T., Niedermeier, R.: Fixed parameter algorithms for Dominating Set and related problems on planar graphs. Algorithmica 33(4), 461–493 (2002) | ||
3. Alber, J., Dorn, B., Niedermeier, R.: A general data reduction scheme for domination in graphs. In: Proc. 32nd SOFSEM. LNCS, vol. 3831, pp. 137-147. Springer, Berlin (2006) | 3. Alber, J., Dorn, B., Niedermeier, R.: A general data reduction scheme for domination in graphs. In: Proc. 32nd SOFSEM. LNCS, vol. 3831, pp. 137-147. Springer, Berlin (2006) | ||
4. Alber, J., Fan, H., Fellows, M.R., Fernau, H., Niedermeier, R., Rosamond, F., Stege, U.: A refined search tree technique for Dominating Set on planar graphs. J. Comput. Syst. Sci. 71(4), 385^05 (2005) | 4. Alber, J., Fan, H., Fellows, M.R., Fernau, H., Niedermeier, R., Rosamond, F., Stege, U.: A refined search tree technique for Dominating Set on planar graphs. J. Comput. Syst. Sci. 71(4), 385^05 (2005) | ||
5. Alber, J., Fellows, M.R., Niedermeier, R.: Polynomial time data reduction for Dominating Set. J. ACM 51 (3), 363-384 (2004) | 5. Alber, J., Fellows, M.R., Niedermeier, R.: Polynomial time data reduction for Dominating Set. J. ACM 51 (3), 363-384 (2004) | ||
6. Baker, B.S.: Approximation algorithms for NP-complete problems on planar graphs. J. ACM 41(1), 153-180 (1994) | 6. Baker, B.S.: Approximation algorithms for NP-complete problems on planar graphs. J. ACM 41(1), 153-180 (1994) | ||
7. Chen, J., Fernau, H., Kanj, I.A., Xia, G.: Parametric duality and kernelization: lower bounds and upper bounds on kernel size. SIAM J. Comput. 37(4), 1077-1106 (2007) | 7. Chen, J., Fernau, H., Kanj, I.A., Xia, G.: Parametric duality and kernelization: lower bounds and upper bounds on kernel size. SIAM J. Comput. 37(4), 1077-1106 (2007) | ||
8. Downey, R.G., Fellows, M.R.: Parameterized Complexity. Springer, New York (1999) | 8. Downey, R.G., Fellows, M.R.: Parameterized Complexity. Springer, New York (1999) | ||
9. Feige, U.: A threshold of lnn for approximating set cover. J. ACM 45(4), 634-652 (1998) | 9. Feige, U.: A threshold of lnn for approximating set cover. J. ACM 45(4), 634-652 (1998) | ||
10. Fomin, F.V., Thilikos, D.M.: Fast parameterized algorithms for graphs on surfaces: Linear kernel and exponential speed-up. In: Proc. 31st ICALP. LNCS, vol. 3142, pp. 581-592. Springer, Berlin (2004) | 10. Fomin, F.V., Thilikos, D.M.: Fast parameterized algorithms for graphs on surfaces: Linear kernel and exponential speed-up. In: Proc. 31st ICALP. LNCS, vol. 3142, pp. 581-592. Springer, Berlin (2004) | ||
11. Guo, J., Niedermeier, R.: Invitation to data reduction and problem kernelization. ACM SIGACT News 38(1), 31-45 (2007) | 11. Guo, J., Niedermeier, R.: Invitation to data reduction and problem kernelization. ACM SIGACT News 38(1), 31-45 (2007) | ||
12. Guo, J., Niedermeier, R.: Linear problem kernels for NP-hard problems on planar graphs. In: Proc. 34th ICALP. LNCS, vol. 4596, pp. 375-386. Springer, Berlin (2007) | 12. Guo, J., Niedermeier, R.: Linear problem kernels for NP-hard problems on planar graphs. In: Proc. 34th ICALP. LNCS, vol. 4596, pp. 375-386. Springer, Berlin (2007) | ||
13. Guo, J., Niedermeier, R., Wernicke, S.: Fixed-parameter tractability results for full-degree spanning tree and its dual. In: Proc. 2nd IWPEC. LNCS, vol. 4196, pp. 203-214. Springer, Berlin (2006) | 13. Guo, J., Niedermeier, R., Wernicke, S.: Fixed-parameter tractability results for full-degree spanning tree and its dual. In: Proc. 2nd IWPEC. LNCS, vol. 4196, pp. 203-214. Springer, Berlin (2006) | ||
14. Haynes, T.W., Hedetniemi, S.T., Slater, P.J.: Domination in Graphs: Advanced Topics. Pure and Applied Mathematics, vol. 209. Marcel Dekker, New York(1998) | 14. Haynes, T.W., Hedetniemi, S.T., Slater, P.J.: Domination in Graphs: Advanced Topics. Pure and Applied Mathematics, vol. 209. Marcel Dekker, New York(1998) | ||
15. Haynes, T.W., Hedetniemi, S.T., Slater, P.J.: Fundamentals of Domination in Graphs. Pure and Applied Mathematics, vol. 208. Marcel Dekker, New York(1998) | 15. Haynes, T.W., Hedetniemi, S.T., Slater, P.J.: Fundamentals of Domination in Graphs. Pure and Applied Mathematics, vol. 208. Marcel Dekker, New York(1998) | ||
16. Niedermeier, R.: Invitation to Fixed-Parameter Algorithms. Oxford University Press, New York (2006) | 16. Niedermeier, R.: Invitation to Fixed-Parameter Algorithms. Oxford University Press, New York (2006) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 10:50, 7 декабря 2024
Ключевые слова и синонимы: доминирующее множество; редукция до ядра задачи; кернелизация
Постановка задачи
NP-полная задача поиска доминирующего множества (DOMINATING SET), как известно, представляет значительную сложность.
Дано: неориентированный граф [math]\displaystyle{ G = (V, E) \; }[/math] и целое число [math]\displaystyle{ k \ge 0 \; }[/math].
Вопрос: существует ли подграф [math]\displaystyle{ S \subseteq V }[/math] с [math]\displaystyle{ |S| \le k \; }[/math], такой, что каждая вершина [math]\displaystyle{ v \in V \; }[/math] входит в S, либо по крайней мере один из ее соседей входит в S?
К примеру, построить оптимизированную версию графа с n вершинами за полиномиальное время можно только с точностью до множителя [math]\displaystyle{ \Theta (log \; n) \; }[/math], если не выполняются некоторые стандартные теоретико-сложностные предположения [9]. В терминах параметризованной сложности эта задача, как было показано в [8], является W[2]-полной. Для планарных графов она по-прежнему является NP-полной, однако в данном случае ситуация оказывается намного проще. В своей основополагающей работе Бэйкер показала, что существует аппроксимационная схема с полиномиальным временем выполнения (PTAS) [6], и что в случае планарных графов эта задача становится разрешимой при помощи алгоритмов с фиксированными параметрами [2, 4]. В частности, задача может иметь решение при использовании достаточно эффективных правил редукции; может быть доказан результат кернелизации (общее описание редукции данных и кернелизации см. в [16]).
Основные результаты
Основная идея редукции данных заключается в предварительной обработке на основе локально применяемых правил упрощения. В качестве примера может служить правило, согласно которому рассматривается локальная окрестность каждой вершины графа. Для этого потребуются следующие определения. Окрестность N(v) произвольной вершины [math]\displaystyle{ v \in V \; }[/math] входного графа разбивается на три непересекающихся множества [math]\displaystyle{ N_1(v) \; }[/math], [math]\displaystyle{ N_2(v) \; }[/math] и [math]\displaystyle{ N_3(v) \; }[/math], зависящих от структуры локальной окрестности. Эти множества таковы:
[math]\displaystyle{ N_1(v) \; }[/math] содержит всех соседей вершины v, от которых идут дуги к вершинам, не являющимся соседями v;
[math]\displaystyle{ N_2(v) \; }[/math] содержит все вершины из [math]\displaystyle{ N(v) \setminus N_1(v) \; }[/math], связанные дугами по крайней мере с одной вершиной из [math]\displaystyle{ N_1(v) \; }[/math];
[math]\displaystyle{ N_3(v) \; }[/math] содержит всех соседей вершины v, не принадлежащих к [math]\displaystyle{ N_1(v) \; }[/math] или [math]\displaystyle{ N_2(v) \; }[/math].
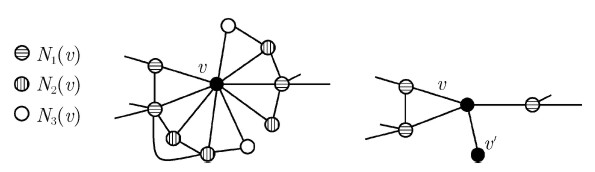
Редукция данных для доминирования в графах
В левой части показано разбиение окрестности вершины v; в правой части показан результат применения приведенного ниже правила редукции данных к этому конкретному (под)графу.
В левой части рисунка показано подобное разбиение. Понятная и полезная интерпретация данного разбиения заключается в том, что вершины из [math]\displaystyle{ N_1(v) \; }[/math] рассматриваются как «выходы», поскольку они имеют прямые связи с «внешним миром» за пределами ближайшей окрестности v; вершины из [math]\displaystyle{ N_2(v) \; }[/math] – как «стражи», поскольку они имеют прямую связь с выходами, а вершины из [math]\displaystyle{ N_3(v) \; }[/math] – как «заключенные», поскольку они не видят «мира» за пределами [math]\displaystyle{ \{ v \} \cup N_1(v) \; }[/math].
Рассмотрим вершину [math]\displaystyle{ w \in N_3(v) \; }[/math]. Такая вершина имеет соседей только из [math]\displaystyle{ \{ v \} \cup N_1(v) \cup N_3(v) \; }[/math]. Следовательно, для того, чтобы доминировать вершину w, по меньшей мере одна вершина из [math]\displaystyle{ \{ v \} \cup N_1(v) \cup N_3(v) \; }[/math] должна входить в доминирующее множество входного графа. Поскольку v может доминировать все вершины, которые были бы доминированы в результате выбора из [math]\displaystyle{ N_1(v) \cup N_3(v) \; }[/math] в доминирующее множество, это дает следующее правило редукции данных:
Если [math]\displaystyle{ N_3(v) \ne \emptyset \; }[/math] для некоторой вершины v, удалить [math]\displaystyle{ N_2(v) \; }[/math] и [math]\displaystyle{ N_3(v) \; }[/math] из G и добавить в G новую вершину v' с дугой {v, v'}.
Новая вершина v' может рассматриваться как «вершина-гаджет», которая «заставляет» выбрать v в доминирующее множество. Корректность этого правила нетрудно проверить, поскольку она сводится к тому, что исходный граф имеет доминирующее множество размера k в том и только том случае, если приведенный в результате редукции граф имеет доминирующее множество размера k. Очевидно, что редукция данных может быть проведена за полиномиальное время [5]. Однако существуют «ромбовидные» структуры, к которым данное правило редукции неприменимо. Для них было предложено несколько более сложное правило, основанное на рассмотрении объединенной окрестности двух вершин [5].
В [5] была доказана справедливость следующей теоремы.
Теорема 1. Планарный граф G = (V, E) может быть за полиномиальное время приведен при помощи редукции к планарному графу G' = (V', E'), такому, что G имеет доминирующее множество размера k в том и только том случае, если G0 имеет доминирующее множество размера k и |V'| = O(k).
Иными словами, теорема утверждает, что задача нахождения доминирующего множества в планарных графах (DOMINATING SET) имеет ядро линейного размера. Значение верхней границы |V'| вначале было установлено равным 335k [5], затем снижено до 67k [7]. Эти результаты могут быть расширены на графы ограниченного рода [10]. Кроме того, подобные же результаты (линейная кернелизация) были недавно получены для задачи нахождения полноразмерного остовного дерева в планарном графе (FULL-DEGREE SPANNING TREE) [13]. Впоследствии эти результаты были обобщены в виде методологической схемы [12].
Применение
Задача нахождения доминирующего множества (DOMINATING SET) считается одной из важнейших задач теории графов [14, 15]. У нее широчайший спектр вариантов применения – от поисков нужного места до биоинформатики.
Открытые вопросы
Наилучшая нижняя граница размера ядра задачи нахождения доминирующего множества в планарных графах (DOMINATING SET) на данный момент равняется 2k [7]. Таким образом, существует большой разрыв между известными верхней и нижней границами. Также были высказаны некоторые соображения о возможности обобщения вышеприведенных правил редукции данных [3]; однако пока перспективы практического применения таких обобщений неясны. Наконец, отдельного исследования заслуживают более глубокие связи между результатами алгоритма PTAS [6] Бэйкер и результатами линейной кернелизации для задачи DOMINATING SET на планарных графах. Классы задач, поддающихся решению обоими способами, были обнаружены в [12]. В недавнем обзоре [11] очерчена область исследования редукции данных и кернелизации в целом и связанные с ними проблемы.
Экспериментальные результаты
Теоретические выкладки сопровождались экспериментальными исследованиями как на искусственно подобранных, так и на реальных данных [1]. Результаты в целом оказались обнадеживающими. Однако структуры типа «решетка» представляют серьезную проблему: на них правила редукции данных практически неэффективны.
См. также
Литература
1. Alber, J., Betzler, N., Niedermeier, R.: Experiments on data reduction for optimal domination in networks. Ann. Oper. Res. 146(1), 105–117 (2006)
2. Alber, J., Bodlaender, H.L., Fernau, H., Kloks, T., Niedermeier, R.: Fixed parameter algorithms for Dominating Set and related problems on planar graphs. Algorithmica 33(4), 461–493 (2002)
3. Alber, J., Dorn, B., Niedermeier, R.: A general data reduction scheme for domination in graphs. In: Proc. 32nd SOFSEM. LNCS, vol. 3831, pp. 137-147. Springer, Berlin (2006)
4. Alber, J., Fan, H., Fellows, M.R., Fernau, H., Niedermeier, R., Rosamond, F., Stege, U.: A refined search tree technique for Dominating Set on planar graphs. J. Comput. Syst. Sci. 71(4), 385^05 (2005)
5. Alber, J., Fellows, M.R., Niedermeier, R.: Polynomial time data reduction for Dominating Set. J. ACM 51 (3), 363-384 (2004)
6. Baker, B.S.: Approximation algorithms for NP-complete problems on planar graphs. J. ACM 41(1), 153-180 (1994)
7. Chen, J., Fernau, H., Kanj, I.A., Xia, G.: Parametric duality and kernelization: lower bounds and upper bounds on kernel size. SIAM J. Comput. 37(4), 1077-1106 (2007)
8. Downey, R.G., Fellows, M.R.: Parameterized Complexity. Springer, New York (1999)
9. Feige, U.: A threshold of lnn for approximating set cover. J. ACM 45(4), 634-652 (1998)
10. Fomin, F.V., Thilikos, D.M.: Fast parameterized algorithms for graphs on surfaces: Linear kernel and exponential speed-up. In: Proc. 31st ICALP. LNCS, vol. 3142, pp. 581-592. Springer, Berlin (2004)
11. Guo, J., Niedermeier, R.: Invitation to data reduction and problem kernelization. ACM SIGACT News 38(1), 31-45 (2007)
12. Guo, J., Niedermeier, R.: Linear problem kernels for NP-hard problems on planar graphs. In: Proc. 34th ICALP. LNCS, vol. 4596, pp. 375-386. Springer, Berlin (2007)
13. Guo, J., Niedermeier, R., Wernicke, S.: Fixed-parameter tractability results for full-degree spanning tree and its dual. In: Proc. 2nd IWPEC. LNCS, vol. 4196, pp. 203-214. Springer, Berlin (2006)
14. Haynes, T.W., Hedetniemi, S.T., Slater, P.J.: Domination in Graphs: Advanced Topics. Pure and Applied Mathematics, vol. 209. Marcel Dekker, New York(1998)
15. Haynes, T.W., Hedetniemi, S.T., Slater, P.J.: Fundamentals of Domination in Graphs. Pure and Applied Mathematics, vol. 208. Marcel Dekker, New York(1998)
16. Niedermeier, R.: Invitation to Fixed-Parameter Algorithms. Oxford University Press, New York (2006)