Декодирование при помощи линейных программ: различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| Строка 38: | Строка 38: | ||
LP-декодер работает следующим образом. Нужно решить линейную программу в (2), чтобы получить <math>y_{LP} \in [0, 1]^n</math>. Если <math>y_{LP}</math> является целым (т. е. все его элементы равны 0 или 1), вывести <math>y_{LP}</math>; в противном случае вывести «ошибка». Согласно определению правильного политопа, если LP-декодер выводит кодовое слово, то оно гарантированно равно ML-кодовому слову y*. Данный факт известен как ''свойство | LP-декодер работает следующим образом. Нужно решить линейную программу в (2), чтобы получить <math>y_{LP} \in [0, 1]^n</math>. Если <math>y_{LP}</math> является целым (т. е. все его элементы равны 0 или 1), вывести <math>y_{LP}</math>; в противном случае вывести «ошибка». Согласно определению правильного политопа, если LP-декодер выводит кодовое слово, то оно гарантированно равно ML-кодовому слову y*. Данный факт известен как ''свойство ML-сертификации''. | ||
'''Сравнение с ML-декодированием''' | '''Сравнение с ML-декодированием''' | ||
Успешным считается декодер, который выдает изначальное кодовое слово, переданное по каналу, а качество алгоритма измеряется вероятностью того, что это произойдет. (Другой распространенной невероятностной мерой является гарантия производительности ''в наихудшем случае'', которая измеряет, сколько инвертированных разрядов может допустить алгоритм, чтобы при этом гарантированно добиться успеха). Заметим, что у* – это ''наиболее вероятное'' переданное кодовое слово | Успешным считается декодер, который выдает изначальное кодовое слово, переданное по каналу, а качество алгоритма измеряется вероятностью того, что это произойдет. (Другой распространенной невероятностной мерой является гарантия производительности ''в наихудшем случае'', которая измеряет, сколько инвертированных разрядов может допустить алгоритм, чтобы при этом гарантированно добиться успеха). Заметим, что у* – это ''наиболее вероятное'' переданное кодовое слово <math>\dot{y}</math>, но не всегда случается так, что <math>y^* = \dot{y}</math>. Однако ни один декодер не может работать лучше ML-декодера, поэтому полезно использовать ML-декодирование в качестве основы для сравнения. | ||
| Строка 53: | Строка 53: | ||
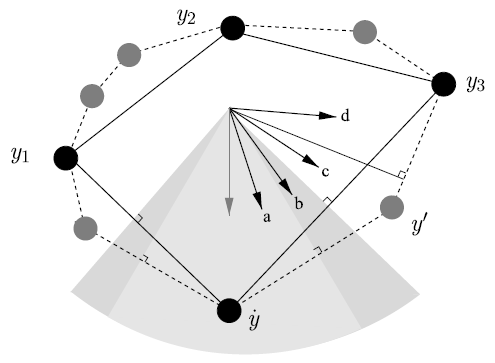
На рисунке 1 представлена геометрическая перспектива LP-декодирования и его связь с точным ML-декодированием. Оба декодера используют одну и ту же целевую функцию LP, но с разными наборами ограничений. При точном ML-декодировании набор ограничений представляет собой выпуклую оболочку C кодовых слов (т. е. множество точек, которые являются выпуклыми комбинациями кодовых слов из C), тогда как в ослабленном LP-декодировании используется более объемный политоп <math>\mathcal{P}</math>. На рис. 1 четыре стрелки, обозначенные (a)-(d), соответствуют различным «зашумленным» версиям целевой функции LP. (a) Если шум очень мал, то целевая функция указывает на переданное кодовое слово <math>\dot{y}</math>, и, следовательно, и ML-декодирование, и LP-декодирование оказываются успешными, поскольку оба представляют переданное кодовое слово | На рисунке 1 представлена геометрическая перспектива LP-декодирования и его связь с точным ML-декодированием. Оба декодера используют одну и ту же целевую функцию LP, но с разными наборами ограничений. При точном ML-декодировании набор ограничений представляет собой выпуклую оболочку <math>\mathcal{C}</math> кодовых слов (т. е. множество точек, которые являются выпуклыми комбинациями кодовых слов из C), тогда как в ослабленном LP-декодировании используется более объемный политоп <math>\mathcal{P}</math>. На рис. 1 четыре стрелки, обозначенные (a)-(d), соответствуют различным «зашумленным» версиям целевой функции LP. (a) Если шум очень мал, то целевая функция указывает на переданное кодовое слово <math>\dot{y}</math>, и, следовательно, и ML-декодирование, и LP-декодирование оказываются успешными, поскольку оба представляют переданное кодовое слово <math>\dot{y}</math> в качестве оптимальной точки. (b) При повышении уровня шума ML-декодирование срабатывает, а LP-декодирование не удается, так как дробная вершина y' является оптимальной для релаксации. (c) При еще большем росте шума ML-декодирование не срабатывает, так как оптимальной теперь является вершина <math>y_3</math>; у LP-декодирования все еще имеется дробный оптимум y', так что эта ошибка в некотором смысле «обнаружена». (d) Наконец, при сильном шуме и ML-декодирование, и LP-декодирование в качестве оптимума выбирают <math>y_3</math>, поэтому оба метода терпят неудачу, и ошибка «не обнаружена». Заметим, что в последних двух случаях (c, d), когда ML-декодирование не срабатывает, неудача LP-декодера в некотором смысле является виной самого кода, а не декодера. | ||
Версия от 16:22, 13 апреля 2023
Ключевые слова и синонимы
LP-декодирование; коды с исправлением ошибок; коды с малой плотностью проверок на четность; LDPC-коды; псевдокодовые слова; распространение доверия
Постановка задачи
Коды с исправлением ошибок являются фундаментальными инструментами, используемыми для передачи цифровой информации по ненадежным каналам. Их изучение восходит к работам Хэмминга и Шеннона, которые использовали их в качестве основы для разработки теории передачи информации. Проблема декодирования исходной информации вплоть до полной реализации потенциала системы коррекции ошибок часто является очень сложной, особенно для современных кодов, которые приближаются к теоретическим пределам каналов связи.
Под LP-декодированием [4, 5, 8] понимается применение релаксации линейного программирования (LP) к задаче декодирования кода с исправлением ошибок. Релаксация линейного программирования является стандартной техникой в алгоритмах аппроксимации и исследовании операций и занимает центральное место при изучении эффективных алгоритмов для поиска хороших (хотя и субоптимальных) решений очень сложных задач оптимизации [13]. LP-декодеры имеют строгие комбинаторные характеристики успеха декодирования, которые можно использовать для анализа эффективности исправления ошибок.
Наибольшую актуальность приобрело LP-декодирование кодов с малой плотностью проверок на четность (LDPC-кодов) [9] в силу высокого качества исправления ими ошибок. Применение LP-декодера для анализа этих кодов особенно привлекательно, потому что стандартные алгоритмы передачи сообщений, такие как распространение доверия (см. [15]), используемые для декодирования, часто трудно поддаются анализу, а производительность LP-декодирования тесно связана с этими методами.
Коды с исправлением ошибок и декодирование по принципу максимального правдоподобия
Вначале представим очень краткий обзор кодов с исправлением ошибок, достаточный для формулировки понятия LP-декодера. Более полное описание кодов с исправлением ошибок в данном контексте можно найти в учебниках, посвященных данному вопросу (например, [11]).
Двоичный код с исправлением ошибок представляет собой подмножество [math]\displaystyle{ C \subseteq \{ 0, 1 \}^n }[/math]. Скорость кода C равна [math]\displaystyle{ r = log(|C|)/n }[/math]. Линейный двоичный код – это линейное подпространство [math]\displaystyle{ \{0, 1 \}^n }[/math]. Кодовое слово представляет собой вектор [math]\displaystyle{ y \in C }[/math]. Заметим, что [math]\displaystyle{ 0^n }[/math] всегда является кодовым словом линейного кода; этот факт пригодится позже. Когда код используется для коммуникации, кодовое слово [math]\displaystyle{ \dot{y} \in C }[/math] передается по зашумленному каналу, в результате чего на приемник поступает некоторое принятое слово [math]\displaystyle{ \hat{y} \in \Sigma^n }[/math], где [math]\displaystyle{ \Sigma }[/math] – некоторый алфавит, зависящий от модели канала. Обычно при LP-декодировании предполагается симметричный канал без запоминания данных. Одним из распространенных примеров таких каналов является двоичный симметричный канал (BSC) с параметром p, который будем называть [math]\displaystyle{ BSC_p }[/math], где 0 < p < 1/2. В канале [math]\displaystyle{ BSC_p }[/math] поддерживается алфавит [math]\displaystyle{ \Sigma = \{ 0, 1 \} }[/math]; для каждого i принятый символ [math]\displaystyle{ \hat{y}_i }[/math] равен [math]\displaystyle{ \dot{y}_i }[/math] с вероятностью p и [math]\displaystyle{ \hat{y}_i = 1 - \dot{y}_i }[/math] в противном случае. LP-декодирование работает с более широким спектром каналов, но далее будет рассматриваться схема [math]\displaystyle{ BSC_p }[/math].
Задача декодирования по принципу максимального правдоподобия (ML) выглядит следующим образом: пусть имеется принятое слово [math]\displaystyle{ \hat{y} \in \{ 0, 1 \}^n }[/math]; необходимо найти кодовое слово [math]\displaystyle{ y^* \in C }[/math], которое с наибольшей вероятностью было передано по каналу. Определив вектор [math]\displaystyle{ \gamma \in \{ -1, +1 \}^n }[/math], где [math]\displaystyle{ \gamma_i = 1 - 2 \hat{y}_i }[/math], легко показать:
(1) [math]\displaystyle{ y^* = \arg min _{y \in C} \sum_i \gamma_i y_i }[/math]
Сложность задачи ML-декодирования сильно зависит от используемого кода. Для простых кодов, таких как код повторения [math]\displaystyle{ C = \{ 0^n, 1^n \} }[/math], она проста; для более сложных (и высокоскоростных) кодов, таких как LDPC-коды, ML-декодирование является NP-трудной задачей [1].
LP-декодирование
Поскольку ML-декодирование в общем случае может быть очень трудным, приходится обращаться к субоптимальным решениям, которые могут быть найдены эффективным образом. Вместо того, чтобы пытаться решить (1), LP-декодирование ослабляет ограничение [math]\displaystyle{ y \in C }[/math] и требует, чтобы выполнялось [math]\displaystyle{ y \in \mathcal{P} }[/math] для некоторого кратко описываемого линейного политопа [math]\displaystyle{ \mathcal{P} \subseteq [ 0, 1 ]^n }[/math], что дает следующую линейную программу:
(2) [math]\displaystyle{ y_{LP} = \arg min _{y \in \mathcal{P}} \sum_{i = 1}^n \gamma_i y_i }[/math]
При этом политоп должен включать все кодовые слова и не включать ни одного целого некодового слова. Такой политоп [math]\displaystyle{ \mathcal{P} }[/math] называется правильным для кода C, если [math]\displaystyle{ \mathcal{P} \cap \{ 0, 1 \}^n = C }[/math].
LP-декодер работает следующим образом. Нужно решить линейную программу в (2), чтобы получить [math]\displaystyle{ y_{LP} \in [0, 1]^n }[/math]. Если [math]\displaystyle{ y_{LP} }[/math] является целым (т. е. все его элементы равны 0 или 1), вывести [math]\displaystyle{ y_{LP} }[/math]; в противном случае вывести «ошибка». Согласно определению правильного политопа, если LP-декодер выводит кодовое слово, то оно гарантированно равно ML-кодовому слову y*. Данный факт известен как свойство ML-сертификации.
Сравнение с ML-декодированием
Успешным считается декодер, который выдает изначальное кодовое слово, переданное по каналу, а качество алгоритма измеряется вероятностью того, что это произойдет. (Другой распространенной невероятностной мерой является гарантия производительности в наихудшем случае, которая измеряет, сколько инвертированных разрядов может допустить алгоритм, чтобы при этом гарантированно добиться успеха). Заметим, что у* – это наиболее вероятное переданное кодовое слово [math]\displaystyle{ \dot{y} }[/math], но не всегда случается так, что [math]\displaystyle{ y^* = \dot{y} }[/math]. Однако ни один декодер не может работать лучше ML-декодера, поэтому полезно использовать ML-декодирование в качестве основы для сравнения.
Рисунок 1. Политоп декодирования [math]\displaystyle{ \mathcal{P} }[/math] (пунктирная линия) и выпуклая оболочка [math]\displaystyle{ \mathcal{C} }[/math] (сплошная линия) кодовых слов [math]\displaystyle{ \dot{y}, y_1, y_2 }[/math] и [math]\displaystyle{ y_3 }[/math]. Также показаны четыре возможных случая (a-d) целевой функции и нормальные конусы для [math]\displaystyle{ \mathcal{P} }[/math] и [math]\displaystyle{ \mathcal{C} }[/math].
На рисунке 1 представлена геометрическая перспектива LP-декодирования и его связь с точным ML-декодированием. Оба декодера используют одну и ту же целевую функцию LP, но с разными наборами ограничений. При точном ML-декодировании набор ограничений представляет собой выпуклую оболочку [math]\displaystyle{ \mathcal{C} }[/math] кодовых слов (т. е. множество точек, которые являются выпуклыми комбинациями кодовых слов из C), тогда как в ослабленном LP-декодировании используется более объемный политоп [math]\displaystyle{ \mathcal{P} }[/math]. На рис. 1 четыре стрелки, обозначенные (a)-(d), соответствуют различным «зашумленным» версиям целевой функции LP. (a) Если шум очень мал, то целевая функция указывает на переданное кодовое слово [math]\displaystyle{ \dot{y} }[/math], и, следовательно, и ML-декодирование, и LP-декодирование оказываются успешными, поскольку оба представляют переданное кодовое слово [math]\displaystyle{ \dot{y} }[/math] в качестве оптимальной точки. (b) При повышении уровня шума ML-декодирование срабатывает, а LP-декодирование не удается, так как дробная вершина y' является оптимальной для релаксации. (c) При еще большем росте шума ML-декодирование не срабатывает, так как оптимальной теперь является вершина [math]\displaystyle{ y_3 }[/math]; у LP-декодирования все еще имеется дробный оптимум y', так что эта ошибка в некотором смысле «обнаружена». (d) Наконец, при сильном шуме и ML-декодирование, и LP-декодирование в качестве оптимума выбирают [math]\displaystyle{ y_3 }[/math], поэтому оба метода терпят неудачу, и ошибка «не обнаружена». Заметим, что в последних двух случаях (c, d), когда ML-декодирование не срабатывает, неудача LP-декодера в некотором смысле является виной самого кода, а не декодера.
Нормальные конусы и С-симметрия
(Отрицательные) нормальные конусы для у (также называемые фундаментальными конусами [10]) определяется следующим образом:
[math]\displaystyle{ N_{\dot{y}}(\mathcal{P}) = \{ \gamma \in \mathbb{R}^n : \sum_i \gamma_i (y_i - \dot{y}_i ) \ge 0 }[/math] для всех [math]\displaystyle{ y \in \mathcal{P} \} }[/math],
[math]\displaystyle{ N_{\dot{y}}(\mathcal{C}) = \{ \gamma \in \mathbb{R}^n : \sum_i \gamma_i (y_i - \dot{y}_i ) \ge 0 }[/math] для всех [math]\displaystyle{ y \in \mathcal{C} \} }[/math].
Заметим, что [math]\displaystyle{ N_{\dot{y}}(\mathcal{P}) }[/math] соответствует множеству векторов затрат [math]\displaystyle{ \gamma }[/math], таких, что [math]\displaystyle{ \dot{y} }[/math] является оптимальным решением (2). Множество [math]\displaystyle{ N_{\dot{y}}(\mathcal{C}) }[/math] имеет аналогичную интерпретацию как множество векторов затрат [math]\displaystyle{ \gamma }[/math], для которых [math]\displaystyle{ \dot{y} }[/math] является кодовым словом при декодировании по принципу максимального правдоподобия (ML). Поскольку [math]\displaystyle{ \mathcal{P} \subset \mathcal{C} }[/math], из определения следует, что [math]\displaystyle{ N_y(\mathcal{C}) \supset N_y(\mathcal{P}) }[/math] для всех [math]\displaystyle{ y \in \mathcal{C} }[/math]. На рис. 1 показаны эти два конуса и их взаимосвязь.
Вероятность успеха LP-декодера равна общей вероятностной мере [math]\displaystyle{ N_{\dot{y}}(\mathcal{P}) }[/math] при распределении на векторах затрат, определяемых каналом. Вероятность успеха ML-декодирования аналогичным образом связана с вероятностной мерой в нормальном конусе [math]\displaystyle{ N_y(\mathcal{C}) }[/math]. Таким образом, расхождение между нормальными конусами [math]\displaystyle{ \mathcal{P} }[/math] и [math]\displaystyle{ \mathcal{C} }[/math] является мерой разрыва между точным ML- и расслабленным LP-декодированием.
Этот анализ выполнен для конкретного переданного кодового слова [math]\displaystyle{ \dot{y} }[/math], но хотелось бы применить его в общем случае. При работе с линейными кодами для большинства декодеров обычно можно предположить, что передается произвольное кодовое слово, поскольку область принятия решения для успешного декодирования симметрична. То же самое справедливо и для LP-декодирования (доказательство см. в [4]), при условии, что политоп [math]\displaystyle{ \mathcal{P} }[/math] является [math]\displaystyle{ \mathcal{C} }[/math]-симметричным, что определяется следующим образом:
Определение 1. Правильный политоп [math]\displaystyle{ \mathcal{P} }[/math] для двоичного кода [math]\displaystyle{ \mathcal{C} }[/math] является [math]\displaystyle{ \mathcal{C} }[/math]-симметричным, если для всех [math]\displaystyle{ y \in \mathcal{P} }[/math] и [math]\displaystyle{ \dot{y} \in \mathcal{C} }[/math] верно [math]\displaystyle{ y \in \mathcal{P} }[/math], где [math]\displaystyle{ y'_i = |y_i - \dot{y}_i | }[/math].
Использование двойной вспомогательной линии для доказательства границ ошибок
Для доказательства успешности LP-декодирования необходимо показать, что [math]\displaystyle{ \dot{y} }[/math] является оптимальным решением LP в (2). Если код [math]\displaystyle{ \mathcal{C} }[/math] линейный, а релаксация – правильная и [math]\displaystyle{ \mathcal{C} }[/math]-симметричная, можно предположить, что [math]\displaystyle{ \dot{y} = 0^n }[/math], а затем показать, что [math]\displaystyle{ 0^n }[/math] является оптимальным. Рассмотрим двойственную задачу LP-декодирования в (2). Если существует достижимая точка двойственной линейной программы, имеющая ту же стоимость (т. е. нулевую), что и точка [math]\displaystyle{ 0^n }[/math] первичной линейной программы, то [math]\displaystyle{ 0^n }[/math] должна быть оптимальной точкой в задаче LP-декодирования. Поэтому, чтобы доказать успешность LP-декодера, достаточно показать точку с нулевой стоимостью двойственной задачи.
(На самом деле, поскольку существование двойственной точки с нулевой стоимостью доказывает только то, что [math]\displaystyle{ 0^n }[/math] является одной из возможно многих оптимальных точек решения прямой задачи, необходимо проявить несколько большую осторожность; в данной статье рассмотрение этого вопроса не предусматривается).
Основные результаты
LP-декодеры в основном изучались в контексте кодов с малой плотностью проверок на четность [9] и их обобщений на коды расширителей [12]. Также были определены LP-декодеры для турбокодов [2], но результаты их применения не столь хороши. В данном кратком изложении основных результатов приводятся границы вероятности ошибки в кодовом слове (WER), или вероятности того, что декодер не выдает переданное слово при наличии шума в канале. Эти границы относятся к конкретным семействам кодов, которые определяются как бесконечное множество кодов возрастающей длины, чья скорость ограничена снизу некоторой константой. Границы даются в асимптотической форме (без инстанцирования констант) и только для двоичного симметричного канала.
Для LP-декодирования и смежных понятий были получены другие важные результаты, которые здесь не упоминаются. Некоторые из этих общих областей рассматриваются в следующем разделе; подробную библиографию можно найти в работе [3].
Коды с малой плотностью проверок на четность
Политоп [math]\displaystyle{ \mathcal{P} }[/math] для LDPC-кодов, впервые определенный в [4, 8, 10], основан на лежащем в основе кода графе Таннера и имеет линейное число переменных и ограничений. Если граф Таннера достаточным образом расширен, то известно, что LP-декодирование способно исправить постоянную долю ошибок в канале и, таким образом, имеет обратный экспоненциальному коэффициент ошибок. Это было доказано с помощью двойного свидетельства:
Теорема 1 [6]. Для любого коэффициента r > 0 имеется константа [math]\displaystyle{ \epsilon \gt 0 }[/math] такая, что существует семейство [math]\displaystyle{ r }[/math] LDPC-кодов длины n, при работе с которым LP-декодер успешен до тех пор, пока каналом инвертированы не более [math]\displaystyle{ \epsilon n }[/math] разрядов. Отсюда следует, что существует константа [math]\displaystyle{ \epsilon' \gt 0 }[/math], такая, что вероятность ошибок в кодовых словах при [math]\displaystyle{ BSC_p }[/math] с [math]\displaystyle{ p \lt \epsilon' }[/math] составляет не более [math]\displaystyle{ 2^{- \Omega(n)} }[/math].
Коды расширителей
Пропускная способность канала связи ограничивает сверху коэффициент, которого можно достичь для семейства кодов и при этом получить вероятность ошибок в кодовых словах, стремящуюся к нулю по мере увеличения длины кода. Пропускная способность [math]\displaystyle{ BSC_p }[/math] обозначается как [math]\displaystyle{ \mathcal{C}_p }[/math]. Используя семейство кодов, основанных на расширителях [12], LP-декодирование может достичь скорости, приближающейся к пропускной способности. Однако, по сравнению с LDPC-кодами, это достигается ценой увеличения сложности декодирования, так как размер линейной программы экспоненциально зависит от разницы между скоростью и пропускной способностью.
Теорема 2 [7]. Для любого p > 0 и любой скорости [math]\displaystyle{ r \lt \mathcal{C}_p }[/math] существует семейство кодов расширителей длины n, такое, что вероятность ошибок в кодовых словах при LP-декодировании в [math]\displaystyle{ BSC_p }[/math] составляет не более [math]\displaystyle{ 2^{- \Omega(n)} }[/math].
Турбокоды
Преимуществом турбокодов [2] является то, что они могут быть кодироваться за линейное время, даже в потоковом режиме. Простой формой турбокода являются коды повторного накопления. LP-декодер для турбокодов и их разновидностей был впервые определен в [4, 5] и основан на решетчатой структуре компонентных сверточных кодов. Из-за некоторых свойств турбокодов невозможно доказать для них столь же сильные границы, как для LDPC-кодов, однако известно следующее:
Теорема 3 [5]. Существует семейство 1/2 - o(1) кодов повторного накопления длины n и константа [math]\displaystyle{ \epsilon \gt 0 }[/math], такая, что в [math]\displaystyle{ BSC_p }[/math] и при [math]\displaystyle{ p \lt \epsilon }[/math] вероятность ошибок LP-декодера в кодовых словах не превышает [math]\displaystyle{ n^{- \Omega(1)} }[/math].
Применение
До недавних пор наибольшее внимание в контексте LP-декодирования уделялось LDPC-кодам. Применение линейных программ для этого семейства кодов не только служит интересной альтернативой более традиционным итерационным методам [15], но и дает полезный инструмент для анализа этих методов; эта идея впервые была рассмотрена в работах [8, 10, 14]. Итеративные методы, такие как распространение доверия, используют локальные вычисления на графе Таннера для обновления аппроксимаций предельных вероятностей каждого бита кода. В этом типе анализа вершины политопа [math]\displaystyle{ \mathcal{P} }[/math] называются псевдокодовыми словами и, как правило, совпадают с неподвижными точками этого итеративного процесса. Другие понятия структур, подобных псевдокодовым словам, такие как множества остановки, также совпадают с вершинами политопа. Понимание этих структур вдохновило разработчиков на создание новых кодов для итеративного и LP-декодирования. (Более полную библиографию этой работы см. в [3]).
Сам метод декодирования может быть расширен многими способами. Добавляя избыточную информацию к описанию кода, можно получить более жесткие наборы ограничений для повышения производительности декодера при исправлении ошибок, хотя и с увеличением сложности. Адаптивные алгоритмы, которые пытаются добавить ограничения «на лету», также исследовались при помощи метода ветвления и границ или других техник. Кроме того, LP-декодирование стало мотивацией к использованию других методов из теории оптимизации при декодировании кодов с исправлением ошибок; соответствующие ссылки см. в [3].
Открытые вопросы
Метод LP-декодирования предлагает простой, эффективный и поддающийся анализу подход к декодированию кодов с исправлением ошибок. Известные на данный момент результаты служат доказательством того, что сильные границы возможны, но пока еще остаются без ответа важные вопросы. Хотя LP-декодеры могут достигать максимальной пропускной способности со временем декодирования, полиномиальным от длины кода, сложность декодера все еще экспоненциально зависит от разрыва между скоростью и пропускной способностью (как и для всех других известных доказуемо эффективных декодеров, также достигающих пропускной способности). Уменьшение этой зависимости было бы большим достижением, и теоретически LP-декодирование могло бы помочь в этом. Также важным направлением дальнейших исследований является повышение доли ошибок, исправляемых LP-декодированием.
Еще один интересный вопрос – существуют ли семейства кодов с линейным расстоянием и постоянной скоростью, для точного декодирования которых можно разработать линейные программы полиномиального размера. Другими словами, есть ли семейства кодов с описанными характеристиками, выпуклые обочки которых имеют полиномиальное число граней? Если да, то для такого семейства LP-декодирование будет эквивалентно ML-декодированию. Если нет, то это служит убедительным доказательством распространенного мнения, заключающегося в том, что субоптимальное декодирование при использовании хороших кодов неизбежно.
Преимуществом LP-декодирования является упомянутое ранее свойство ML-сертификации, которым не обладает большинство других стандартных субоптимальных декодеров. Это свойство открывает возможность использования широкого спектра эвристик для улучшения производительности декодирования, некоторые из которых были проанализированы, но в основном остаются неизученными.
LP-декодирование исследовалось большей частью для LDPC-кодов в симметричных каналах без запоминания данных. Линейные программы для турбокодов были определены, но доказанные до сих пор границы ошибок не являются удовлетворительным объяснением превосходной производительности, наблюдаемой на практике. Другие типы кодов и каналов были удостоены гораздо меньшего внимания или вообще остались вне поля зрения.
См. также
- Декодирование кодов Рида–Соломона
- Изучение высоких коэффициентов Фурье булевых функций
- Проверка линейности / тестирование кодов Адамара
- Списочное декодирование в приближении к максимальной пропускной способности: свернутые коды Рида–Соломона
Литература
1. Berlekamp, E., McEliece, R., van Tilborg, H.: On the inherent intractability of certain coding problems. IEEE Trans. Inf. Theory 24,384-386(1978)
2. Berrou, C., Glavieux, A., Thitimajshima, P.: Near Shannon limit error-correcting coding and decoding: turbo-codes. In: Proc. IEEE Int. Conf. Comm. (ICC), pp. 1064-1070. Geneva, 23-26 May 1993
3. Boston, N., Ganesan, A., Koetter, R., Pazos, S., Vontobel, P.: Papers on pseudocodewords. HP Labs, Palo Alto. http://www.pseudocodewords.info.
4. Feldman, J.: Decoding Error-Correcting Codes via Linear Programming. Ph.D. thesis, Massachusetts Institute of Technology (2003)
5. Feldman, J., Karger, D.R.: Decoding turbo-like codes via linear programming. In: Proc. 43rd annual IEEE Symposium on Foundations of Computer Science (FOCS), Vancouver, 16-19 November 2002
6. Feldman, J., Malkin, T., Servedio, R.A., Stein, C., Wainwright, M.J.: LP decoding corrects a constant fraction of errors. In: Proc. IEEE International Symposium on Information Theory, Chicago, 27 June - 2 July 2004
7. Feldman, J., Stein, C.: LP decoding achieves capacity. In: Symposium on Discrete Algorithms (SODA '05), Vancouver, January (2005)
8. Feldman, J., Wainwright, M.J., Karger, D.R.: Using linear programming to decode linear codes. In: 37th annual Conf. on Information Sciences and Systems (CISS '03), Baltimore, 12-14 March 2003
9. Gallager, R.: Low-density parity-check codes. IRE Trans. Inform. Theory, IT-8 , pp. 21 -28 (1962)
10. Koetter, R., Vontobel, P.: Graph covers and iterative decoding of finite-length codes. In: Proc. 3rd International Symposium on Turbo Codes and Related Topics, pp. 75-82, September 2003. Brest, France (2003)
11. MacWilliams, F.J., Sloane, N.J.A.: The Theory of Error Correcting Codes. North-Holland, Amsterdam (1981)
12. Sipser, M., Spielman, D.: Expander codes. IEEE Trans. Inf. Theory 42,1710-1722(1996)
13. Vazirani, V.V.: Approximation Algorithms. Springer, Berlin (2003)
14. Wainwright, M., Jordan, M.: Variational inference in graphical models: the view from the marginal polytope. In: Proc. 41st Allerton Conf. on Communications, Control, and Computing, Monticello, October (2003)
15. Wiberg, N.: Codes and Decoding on General Graphs, Ph. D. thesis, Linkoping University, Sweden (1996)