Сортировка при помощи транспозиций и обращений (коэффициент аппроксимации 1,5): различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| Строка 11: | Строка 11: | ||
[[Файл:Sort_transp_1.png]] | [[Файл:Sort_transp_1.png]] | ||
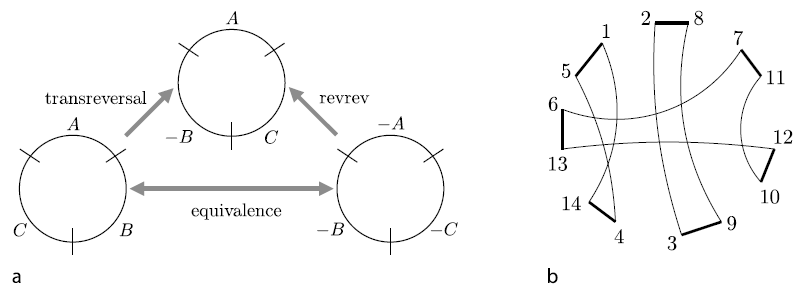
Рисунок 1. (a) Эквивалентность операций transreversal и revrev на циклических перестановках. (b) Граф разрывов <math>G(\pi)</math> перестановки <math>\pi = [1, -4, 6, -5, 2, -7, -3]</math>, для которого <math>f(\pi) = [1, 2, 8, 7, 11, 12, 10, 9, 3, 4, 14, 13, 6, 5]</math>. <math>G(\pi)</math> удобно изображать на круге | Рисунок 1. (a) Эквивалентность операций transreversal и revrev на циклических перестановках. (b) Граф разрывов <math>G(\pi)</math> перестановки <math>\pi = [1, -4, 6, -5, 2, -7, -3]</math>, для которого <math>f(\pi) = [1, 2, 8, 7, 11, 12, 10, 9, 3, 4, 14, 13, 6, 5]</math>. <math>G(\pi)</math> удобно изображать на круге таким образом, что его ''черные ребра'' (т. е. ''толстые линии'') располагаются на окружности, а ''серые'' (т. е. ''тонкие'') являются хордами | ||
== Основные результаты == | == Основные результаты == | ||
Версия от 07:58, 1 марта 2019
Ключевые слова и синонимы
Перестройка генома
Постановка задачи
Одним из наиболее многообещающих способов определения эволюционного расстояния между двумя организмами является сравнение порядка появления идентичных (например, ортологичных) генов в их геномах. Соответствующая задача перестройки генома заключается в нахождении кратчайшей последовательности операций перегруппировки, при помощи которых один геном можно перестроить в другой. В работе [8] Хартман и Шаран предложили алгоритм 1,5-аппроксимации для решения задачи сортировки при помощи транспозиций, транспозиций-обращений и двойных обращений, улучшив ранее полученный коэффициент аппроксимации для этой задачи. Их алгоритм также работает быстрее современных аналогов, требуя [math]\displaystyle{ O(n^{3/2} \sqrt{log \; n}) }[/math] времени для n генов.
Нотация и определение
Перестановка со знаками [math]\displaystyle{ \pi = [ \pi_1, \pi_2, ..., \pi_n] }[/math] на [math]\displaystyle{ n (\pi) = n }[/math] элементах представляет собой перестановку, в которой каждому элементу присвоен знак – плюс или минус. Сегментом [math]\displaystyle{ \pi }[/math] является последовательность последовательных элементов [math]\displaystyle{ \pi_i, \pi_{i + 1}, ..., \pi_k }[/math], где [math]\displaystyle{ 1 \le i \le k \le n }[/math]. Обращение [math]\displaystyle{ \rho }[/math] представляет собой операцию, которая меняет порядок элементов в сегменте на противоположный и при этом переключает их знаки. Два сегмента [math]\displaystyle{ \pi_i, \pi_{i + 1}, ..., \pi_k }[/math] и [math]\displaystyle{ \pi_j, \pi_{j + 1}, ..., \pi_l }[/math], называются смежными, если j = k + 1 или i = l + 1. Транспозиция [math]\displaystyle{ \tau }[/math] представляет собой операцию, переставляющую друг с другом два смежных (непересекающихся) сегмента. Транспозиция-обращение (transreversal) [math]\displaystyle{ \tau \rho_{A, B} }[/math] ([math]\displaystyle{ \tau \rho_{B, A} }[/math], соответственно) представляет собой транспозицию, которая переставляет два сегмента A и B и при этом выполняет обращение A (соответственно, B). Операция двойного обращения (revrev) [math]\displaystyle{ \rho \rho }[/math] выполняет обращение каждого из двух смежных сегментов (без перестановки их друг с другом). Задача нахождения кратчайшей последовательности операций транспозиции, транспозиции-обращения и двойного обращения, преобразующей заданную перестановку в тождественную, называется задачей сортировки при помощи транспозиций, транспозиций-обращений и двойных обращений. Длина кратчайшей сортирующей последовательности обращений называется расстоянием обращения [math]\displaystyle{ \pi }[/math] и обозначается как [math]\displaystyle{ d(\pi) }[/math].
Рисунок 1. (a) Эквивалентность операций transreversal и revrev на циклических перестановках. (b) Граф разрывов [math]\displaystyle{ G(\pi) }[/math] перестановки [math]\displaystyle{ \pi = [1, -4, 6, -5, 2, -7, -3] }[/math], для которого [math]\displaystyle{ f(\pi) = [1, 2, 8, 7, 11, 12, 10, 9, 3, 4, 14, 13, 6, 5] }[/math]. [math]\displaystyle{ G(\pi) }[/math] удобно изображать на круге таким образом, что его черные ребра (т. е. толстые линии) располагаются на окружности, а серые (т. е. тонкие) являются хордами