Геометрическая протяженность геометрических сетей

Ключевые слова и синонимы

Обход; коэффициент растяжения; показатель растяжения

Постановка задачи

Городские системы улично-дорожной сети можно моделировать плоскими геометрическими сетями G = (V, E), ребра которых [math]\displaystyle{ e \in E \; }[/math] представляют собой кусочно гладкие кривые, соединяющие вершины [math]\displaystyle{ v \in V \subset \mathbb{R}^2 \; }[/math].

Ребра не пересекаются нигде, кроме общих конечных точек в V. Поскольку вдоль улиц стоят дома, качество подобной сети может измеряться в длине путей между любыми двумя произвольными точками p и q в G.

Обозначим за [math]\displaystyle{ \xi_G (p, q) \; }[/math] кратчайший путь из p в q по G. Тогда

(1) [math]\displaystyle{ \delta(p, q) := \frac{| \xi_G (p, q) |}{|pq|} }[/math]

представляет собой обход, по которому необходимо идти при перемещении по сети G из точки p в точку q, вместо того чтобы пройти напрямую. Здесь |.| обозначает евклидову длину. Геометрическая протяженность сети G задается соотношением

(2) [math]\displaystyle{ \delta(G) := sup_{p \ne q \in G} \delta(p, q) }[/math].

Это определение отличается от понятия коэффициента растяжения, использовавшегося в контексте остовных деревьев; подробнее об этом – в монографиях Эпштейна [6] или Нарасимхана и Смида [11]. В последней рассматриваются только пути между вершинами [math]\displaystyle{ p, q \in V \; }[/math], тогда как понятие геометрической протяженности включает также все точки на ребрах. Следовательно, коэффициент растяжения треугольника T равен 1, однако его геометрическая протяженность задается формулой [math]\displaystyle{ \delta(T) = \sqrt{2 / (1 - cos \; \alpha)} \ge 2 }[/math], где [math]\displaystyle{ \alpha \le 60^\circ \; }[/math] - самый острый угол T.

Пусть дано конечное множество S точек на плоскости. Требуется найти конечную геометрическую сеть, содержащую S, геометрическая протяженность которой насколько возможно мала. Значение

[math]\displaystyle{ \Delta(S) := inf \{ \delta(G); G \; }[/math] – конечная плоская геометрическая сеть, содержащая S}

называется геометрической протяженностью множества точек S. Задача заключается в вычислении или ограничении [math]\displaystyle{ \Delta(S) \; }[/math] для данного множества S.

Основные результаты

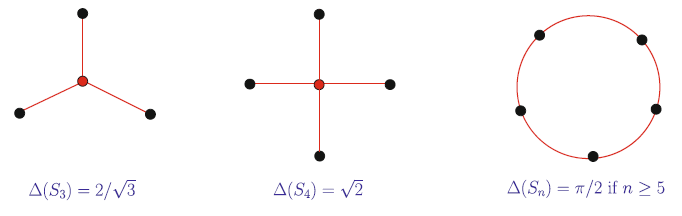
Теорема 1 [4]. Обозначим за [math]\displaystyle{ S_n \; }[/math] множество углов правильного n-угольника. Тогда [math]\displaystyle{ \Delta(S_3) = 2 / \sqrt{3}, \Delta(S_4) = \sqrt{2}, \Delta(S_n) = \pi / 2 \; }[/math] для всех [math]\displaystyle{ n \ge 5 \; }[/math].

Сети, в которых достигаются такие минимальные значения, изображены на рис. 1. В доказательстве минимальности используются следующие две леммы, которые интересны и сами по себе. Лемма 1 была независимо получена Ароновым и др. [1].

Рисунок 1. Вложения с минимальной протяженностью в регулярные множества точек

Лемма 1. Пусть T – дерево, содержащее [math]\displaystyle{ S_n \; }[/math]. Тогда [math]\displaystyle{ \delta(T) \ge n / \pi }[/math].

Лемма 2 следует из результата, полученного Громовым [7]. Ее проще доказать при помощи формулы Коши для расчета площади поверхности [4].

Лемма 2. Обозначим за C простую замкнутую кривую на плоскости. Тогда [math]\displaystyle{ \delta(C) \ge \pi / 2 }[/math].

Очевидно, для круга лемма 2 выполняется со знаком равенства. Из следующей леммы следует, что круг – единственная замкнутая кривая, имеющая минимальную геометрическую протяженность [math]\displaystyle{ \pi / 2 \; }[/math].

Лемма 3 [3]. Обозначим за C простую замкнутую кривую на плоскости с геометрической протяженностью, меньшей [math]\displaystyle{ \pi / 2 + \epsilon (\delta) }[/math]. В таком случае C содержится в кольце ширины [math]\displaystyle{ \delta \; }[/math].

Для точек, имеющих общее положение, вычисление геометрической протяженности оказывается весьма сложным. Решение этой задачи полностью известно только для множеств S = {A, B, C} величины 3.

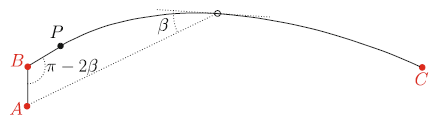
Теорема 2 [5]. Плоская геометрическая сеть с минимальной геометрической протяженностью, содержащая три заданные точки {A, B, C}, представляет собой либо отрезок прямой, либо дерево Штейнера, представленное на рис. 1, либо простой путь, состоящий из двух отрезков прямых и одного сегмента экспоненциальной спирали, см. рис. 2.

Оптимальный путь, представленный на рис. 2, содержит вершину Штейнера степени 2, P, расположенную на расстоянии |AB| от B. Путь от A к B и от B к P идет по прямой. От P к C он идет по экспоненциальной спирали с центром в A.

Рисунок 2. Вложение с минимальной протяженностью для точек A, B и C

Следующий результат задает верхнюю и нижнюю границы A(S).

Теорема 3 [4]. Для каждого конечного множества точек S выполняется соотношение [math]\displaystyle{ \Delta(S) \lt 1.678 \; }[/math].

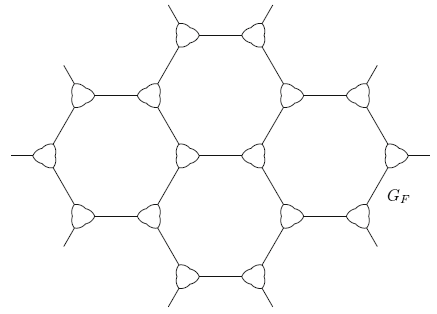
Для доказательства верхней границы заменим каждую вершину шестиугольной черепицы [math]\displaystyle{ \mathbb{R}^2 \; }[/math] определенной замкнутой кривой Зиндлера (по определению, все пары точек, делящие пополам периметр кривой Зиндлера, находятся на одинаковом расстоянии). В результате получаем сеть [math]\displaystyle{ G_F \; }[/math] с геометрической протяженностью, приблизительно равной 1.6778, см. рис. 3. Пусть дано конечное множество точек S. Применим небольшую деформацию к масштабированной версии [math]\displaystyle{ G_F \; }[/math], такую, чтобы все точки S лежали в конечной части, G, деформированного множества. Согласно теореме Дирихле о приближении действительных чисел рациональными, достаточно выполнить деформацию, малую относительно размера ячейки, так что на протяженность она не повлияет. Определение и свойства кривых Зиндлера см. в [8].

Рисунок 3. Сеть с геометрической протяженностью, приблизительно равной 1,6778

Теорема 4 [3]. Существует конечное множество точек S, такое, что [math]\displaystyle{ \Delta(S) \gt (1 + 10^{-11}) \; \pi / 2 }[/math].

Теорема 4 выполняется для множества точек S размером 19 x 19 вершин целочисленной решетки. Грубо говоря, если S заключено в геометрическую сеть G с протяженностью, близкой к [math]\displaystyle{ \pi / 2 \; }[/math], то, согласно лемме 3, границы граней G должны быть заключены в небольшом кольце. Для получения внутреннего и внешнего кругов этого кольца следует воспользоваться утверждением Купербергов и др. [9], гласящим, что расширение упаковки дисков радиуса [math]\displaystyle{ \le 1 \; }[/math] на определенный коэффициент не может покрыть квадрат со стороной 4.

Применение

Понятие геометрической протяженности применяется в теории узлов; см, например, Куснер и Салливан [10], Денн и Салливан [2]. Применительно к градостроительному проектированию вышеприведенные соображения задают основные границы протяженности при соединении заданных площадок при помощи плоских геометрических сетей.

Открытые вопросы

Для практического применения в дополнение к верхним границам геометрической протяженности пригодились бы верхние границы веса (т.е. общей длины ребер) геометрической сети. Некоторые теоретические вопросы также требуют дополнительного исследования. Всегда ли A(S) достигается для конечной сети? Как вычислить (точно или приближенно) A(S) для заданного конечного множества S? Чему равняется точное значение sup{A(S); S finite}?

См. также

• Протяженность геометрических сетей

Литература

1. Aronov, B., de Berg, M., Cheong, O., Gudmundsson, J., Haverkort, H., Vigneron, A.: Sparse Geometric Graphs with Small Dilation. 16th International Symposium ISAAC 2005, Sanya. In: Deng, X., Du, D. (eds.) Algorithms and Computation, Proceedings. LNCS, vol. 3827, pp. 50-59. Springer, Berlin (2005)

2. Denne, E., Sullivan, J.M.: The Distortion of a Knotted Curve. http://www.arxiv.org/abs/math.GT/0409438 (2004)

3. Dumitrescu, A., Ebbers-Baumann, A., GrCine, A., Klein, R., Rote, G.: On the Geometric Dilation of Closed Curves, Graphs, and Point Sets. Comput. Geom. Theory Appl. 36(1), 16-38(2006)

4. Ebbers-Baumann, A., GrCine, A., Klein, R.: On the Geometric Dilation of Finite Point Sets. Algorithmica 44(2), 137-149 (2006)

5. Ebbers-Baumann, A., Klein, R., Knauer, C., Rote, G.: The Geometric Dilation of Three Points. Manuscript (2006)

6. Eppstein, D.: Spanning Trees and Spanners. In: Sack, J.-R., Urrutia, J. (eds.) Handbook of Computational Geometry, pp. 425-461. Elsevier, Amsterdam (1999)

7. Gromov, M.: Structures Metriques desVarietes Riemanniennes. Textes Math. CEDIX, vol. 1. F. Nathan, Paris (1981)

8. GrCine, A.: Geometric Dilation and Halving Distance. Ph. D. thesis, Institut fur Informatik I, Universitat Bonn (2006)

9. Kuperberg, K., Kuperberg, W., Matousek, J., Valtr, P.: Almost Tiling the Plane with Ellipses. Discrete Comput. Geom. 22(3), 367-375(1999)

10. Kusner, R.B., Sullivan, J.M.: On Distortion and Thickness of Knots. In: Whittington, S.G. et al. (eds.) Topology and Geometry in Polymer Science. IMA Volumes in Math. and its Applications, vol. 103, pp. 67-78. Springer, New York (1998)

11. Narasimhan, G., Smid, M.: Geometric Spanner Networks. Cambridge University Press(2007)