Усиление степени сжатия текста

Ключевые слова и синонимы

Модели сжатия высокого порядка; сжатие с учетом контекста

Постановка задачи

Неформально техника усиления представляет собой метод, который при применении к определенному классу алгоритмов повышает их эффективность. Повышение должно быть доказуемым и четко определенным в виде одного или нескольких параметров, характеризующих эффективность работы алгоритма. Примеры подобных «усилителей» можно найти в сегментах рандомизированных алгоритмов (здесь усилитель позволяет превратить алгоритм BPP в RP [6]) и теории вычислительного обучения (в данном случае усилитель позволяет повысить точность прогнозирования у слабого обучающего алгоритма [10]). Задача усиления сжатия заключается в разработке техники, повышающей эффективность сжатия широкого класса алгоритмов. В частности, результатом работы Ферраджины и др. явилась обобщенная техника, позволяющая «заставить» компрессор, не использовавший контекстной информации вовсе, всегда использовать наилучший возможный контекст.

Классические алгоритмы Хаффмана и арифметического кодирования [1] могут служить примерами статистических алгоритмов сжатия, обычно кодирующих входной символ в соответствии с общей частотой его вхождения в данных, подлежащих сжатию. [Динамические версии этих алгоритмов рассматривают частоту схождения символа в уже просканированной порции входных данных.] Этот подход эффективен и прост в реализации, однако обеспечивает невысокий уровень сжатия. Эффективность работы статистических алгоритмов сжатия можно повысить в результате использования моделей более высокого порядка, получающих более качественную оценку частоты встречаемости входных символов. Алгоритм сжатия PPM [9] реализует эту идею за сбора данных о частоте вхождения всех символов, попадающих в любой контекст длины k, и сжатия их при помощи арифметического кодирования. Длина контекста k представляет собой параметр алгоритма, который определяется подлежащими сжатию данными: он будет разным при сжатии текста на английском языке, последовательности ДНК или документа в формате XML. Можно привести и другие примеры сложных программ сжатия, таких как алгоритмы Лемпеля-Зива и Барроуза-Уилера [9], использующих информацию о контексте неявным образом. Все эти алгоритмы, учитывающие контекст, хороши по критерию эффективности работы, однако сложны для реализации и анализа.

Применение техники усиления Ферраджины и др. к алгоритмам Хаффмана и арифметического кодирования позволяет получить новый алгоритм сжатия со следующими характеристиками:

(i) новый алгоритм использует усиленный алгоритм сжатия в качестве черного ящика;

(ii) новый алгоритм выполняет сжатие в стиле PPM, автоматически выбирая оптимальное значение k;

(iii) асимптотическая эффективность нового алгоритма по соотношению времени и памяти соответствует эффективности усиленного алгоритма сжатия.

В следующих разделах будет изложено точное формальное обоснование перечисленных характеристик.

Основные результаты

Нотация. Эмпирическая энтропия

Пусть s – строка над алфавитом $\mathrm{\Sigma }=\{a_1,...,a_h\}$. Обозначим для каждого $a_i\in \mathrm{\Sigma }$ за $n_i$ количество вхождений $a_i$ в s. Эмпирическая энтропия нулевого порядка строки s определяется как $H_0(s)=-\sum _{i=1}^h(n_i/|s|)log(n_i/|s|)$, где все алгоритмы берутся по основанияю 2, а 0 log 0 = 0. Хорошо известно, что $H_0$ представляет собой максимальный уровень сжатия, которого можно достичь при использовании уникального декодируемого кода, в котором каждому символу алфавита назначается уникальное кодовое слово. Более высокой степени сжатия можно достичь, если кодовое слово символа зависит от k символов, следующих за ним (то есть от его контекста). [Большинство алгоритмов сжатия данных обычно рассматривают контекст, предшествующий кодируемым символам. В данном описании используется нестандартный «прямой» контекст для упрощения нотации в последующих разделах. Работа с «прямым» контекстом эквивалентна работе с традиционным «обратным» контекстом для обращенной строки s (подробнее см. в [3]).] Определим $w_s$ как строку единичных символов, непосредственно предшествующих вхождениям w в s. Например, для s = bcabcabdca получим $c{a}_s=bbd$. Значение

(1) $H_k(s)=\frac{1}{|s|}\sum _{w\in {\mathrm{\Sigma }}^k}|w_s|H_0(w_s)$

представляет эмпирическую энтропию k-го порядка для s и является нижней границей степени сжатия, которой можно достичь при использовании кодовых слов, которые зависят только от k символов, непоследственно следующих за кодируемым.

Пример 1. Пусть строка s = mississippi. Для k = 1 имеем $i_s=mssp,s_s=isis,p_s=ip$. Следовательно, $H_1(s)=\frac{4}{11}{H}_0(mssp)+\frac{4}{11}{H}_0(isis)+\frac{2}{11}{H}_0(ip)=\frac{6}{11}+\frac{4}{11}+\frac{2}{11}=\frac{12}{11}.$

Отметим, что эмпирическая энтропия определяется для любой строки и может использоваться для измерения эффективности алгоритмов сжатия без каких-либо предположений о входных данных. К сожалению, для некоторых строк (с очень высокой сжимаемостью) эмпирическая энтропия обеспечивает слишком консервативное значение нижней границы. Например, для $s=a^n$ имеет место $|s|H_k(s)=0$ для любого $k\ge 0$. Чтобы лучше справляться со строками с высокой сжимаемостью, в работе [7] было введено понятие модифицированной эмпирической энтропии нулевого порядка $H_0^{\ast }(s)$, имеющей следующее свойство: $|s|H_0^{\ast }(s)$ по меньшей мере равно количеству бит, необходимых для записи длины s в двоичной форме. Модифицированная эмпирическая энтропия k-го порядка $H_k^{\ast }$ определяется как максимальная степень сжатия, которой можно достичь при просмотре не более чем k символов, следующих за кодируемым.

Преобразование Барроуза-Уилера

Пусть дана строка s. Преобразование Барроуза-Уилера [2] (bwt) включает три основных этапа:

(1) добавить в концу строки s специальный символ $, который меньше любого другого символа в $\mathrm{\Sigma }$;

(2) сформировать концептуальную матрицу $\mathcal{M}$, строки которой содержат круговые сдвиги строки s$, отсортированные в лексикографическом порядке;

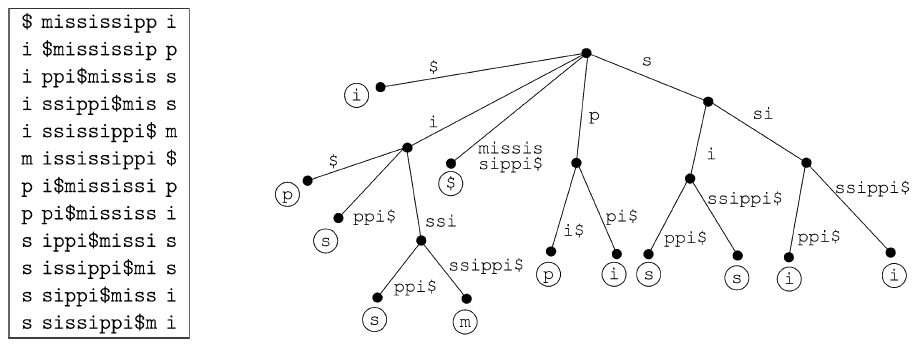
(3) построить преобразованный текст $\hat{s}=bwt(s)$, взяв последний столбец матрицы $\mathcal{M}$ (см. рис. 1).

В работе [2] Барроуз и Уилер доказали, что $\hat{s}$ является перестановкой s и что можно восстановить s из $\hat{s}$ за время O(|s|).

Чтобы убедиться в мощи преобразования bwt, рассмотрим ситуацию с точки зрения эмпирической энтропии. Зафиксируем целое положительное число k. Первые k столбцов матрицы bwt содержат все подстроки s длины k, лексикографически упорядоченные (а также k подстрок, содержащих символ $). Для любой подстроки w строки s длины k символы, непосредственно предшествующие каждому вхождению w в s, сгруппированы вместе в множество последовательных позиций в $\hat{s}$, поскольку они являются последними символами строк матрицы $\mathcal{M}$, которым предшествуют символы w. Используя нотацию, предложенную при определении ${Н}_k$, можно перефразировать это свойство так, чтобы символы $w_s$ были последовательными в $\hat{s}$ или, что эквивалентно, чтобы $\hat{s}$ содержало в качестве подстроки перестановку ${\pi }_w(w_s)$ строки $w_s$.

Пример 2. Пусть s = mississippi и k = 1. На рис. 1 показано, что $\hat{s}[1,4]=pssm$ является перестановкой $i_s=mssp$. Кроме того, $\hat{s}[6,7]=pi$ является перестановкой $p_s=ip$, а $\hat{s}[8,11]=ssii$ – перестановкой $s_s=isis$.

Поскольку перестановка строки не меняет ее (модифицированной) эмпирической энтропии нулевого порядка (то есть $H_0({\pi }_w(w_s))=H_0(w_s))$), преобразование Барроуза-Уилера может рассматриваться как способ свести задачу сжатия строки s вплоть до энтропии k-го порядка к задаче сжатия различных фрагментов $\hat{s}$ вплоть до их энтропии нулевого порядка. Чтобы убедиться в этом, рассмотрим разбиение $\hat{s}$ на подстроки ${\pi }_w(w_s)$, изменяя w над ${\mathrm{\Sigma }}^k$. Из этого следует, что $\hat{s}=\underset{w\in {\mathrm{\Sigma }}^k}{⨆}{\pi }_w(w_s)$, где $⨆$ – оператор конкатенации над строками. [Помимо $\underset{w\in {\mathrm{\Sigma }}^k}{⨆}{\pi }_w(w_s)$, строка $\hat{s}$ также содержит последние k символов s (не входящие ни в какой $w_s$) и специальный символ $. Для простоты в дальнейшем изложении эти символы будут игнорироваться.]

Из (1) следует, что $\sum _{w\in {\mathrm{\Sigma }}^k}|{\pi }_w(w_s)|H_0({\pi }_w(w_s))=\sum _{w\in {\mathrm{\Sigma }}^k}|w_s|H_0(w_s)=|s|H_k(s)$.

Следовательно, для сжатия строки s вплоть до $|s|H_k(s)$ достаточно сжать каждую ее подстроку ${\pi }_w(w_s))$ вплоть до эмпирической энтропии нулевого порядка. Заметим, однако, что при использовании вышеприведенной схемы параметр k необходимы выбрать заранее. Более того, подобную схему нельзя применить к $H_k^{\ast }$, определенной в терминах контекстов длины не более k. В результате на данный момент не известно эффективной процедуры для вычисления разбиения $\hat{s}$ согласно $H_k^{\ast }(s)$. Усилитель сжатия [3] представляет собой естественное дополнение bwt и позволяет сжимать любую строку s до $H_k(s)$ (или $H_k^{\ast }(s)$) одновременно для всех $k\ge 0$.

Алгоритм усиления степени сжатия

Важнейшим компонентом алгоритма усиления степени сжатия является взаимосвязь между матрицей bwt и такой структурой данных, как суффиксное дерево. Обозначим за $\mathcal{T}$ суффиксное дерево строки s$. У $\mathcal{T}$ имеется |s| + 1 листьев, по одному на суффикс s$, а его ребра помечены подстроками s$ (см. рис. 1). Любая вершина u дерева $\mathcal{T}$ неявно ассоциируется с подстрокой s$, задаваемой конкатенацией меток ребер на нисходящем пути от корня $\mathcal{T}$ к u. В рамках этой неявной ассоциации листья $\mathcal{T}$ соответствуют суффиксам s$. Предположим, что ребра суффиксного дерева лексикографически отсортированы. Поскольку каждая строка матрицы bwt имеет префикс в виде суффикса s$, а строки лексикографически отсортированы, i-й лист суффиксного дерева (считая справа налево) соответствует i-й строке матрицы bwt. Ассоциируем с i-м листом $\mathcal{T}$ i-й символ $\hat{s}=bwt(s)$. На рисунке эти символы представлены внутри кружков.

Для любой вершины суффиксного дерева u обозначим за $\hat{s}(u)$ подстроку $\hat{s}$, полученную в результате конкатенации, слева направо, символов, ассоциированных с листьями, являющимися потомками вершины u. Разумеется, $\hat{s}⟨root(\mathcal{T})⟩=\hat{s}$. Подмножество $\mathcal{L}$ вершин $\mathcal{T}$ называется листовым покрытием, если каждый лист суффиксного дерева имеет уникального предка в $\mathcal{L}$. Любое листовое покрытие $\mathcal{L}=\{u_1,...,u_p\}$ естественным образом порождает разбиение листьев $\mathcal{T}$. В силу взаимосвязи между $\mathcal{T}$ и матрицей bwt также имеется разбиение $\hat{s}$, а именно – $\{\hat{s}⟨u_1⟩,...,\hat{s}⟨u_p⟩\}$.

Пример 3. Рассмотрим суффиксное дерево на рисунке. Листовое покрытие состоит из всех вершин, имеющих глубину 1. Разбиение $\hat{s}$, порожденное этим листовым покрытием, выглядит как {i, pssm, $; pi, ssii}.

Матрица bwt (слева) и суффиксное дерево (справа) для строки s = mississippi$. Выходным значением алгоритма bwt является последний столбец матрицы bwt, т.е., в данном случае, $\hat{s}=bwt(s)=ipssm\$pissii$.

Обозначим за C функцию, которая ассоциирует с каждой строкой x над $\mathrm{\Sigma }\cup \{\$\}$ положительное вещественное значение C(x). Для любого листового покрытия $\mathcal{L}$ определим его стоимость как $C(\mathcal{L})=\sum _{u\in \mathcal{L}}C(\hat{s}⟨u⟩)$ – иными словами, стоимость листового покрытия $\mathcal{L}$ равна сумме стоимостей строк в разбиении, порожденном $\mathcal{L}$. Листовое покрытие ${\mathcal{L}}_{m}in$ называется оптимальным относительно $CеслиC({\mathcal{L}}_{m}in)\le C(\mathcal{L})$ для любого листового покрытия $\mathcal{L}$.

Пусть A – алгоритм сжатия, такой, что для любой строки x размер ее выходного значения ограничен $|x|H_0(x)+\eta |x|+\mu$ бит, где $\eta$ и $\mu$ – константы. Определим функцию стоимости $C_A(x)=|x|H_0(x)+\eta |x|+\mu$. В работе [3] Ферраджина и коллеги используют жадный алгоритм с линейным временем выполнения, вычисляющий оптимальное листовое покрытие ${\mathcal{L}}_{min}$ относительно $C_A$. Авторы работы [3] также показали, что для любого $k\ge 0$ существует листовое покрытие ${\mathcal{L}}_k$ стоимостью $C_A({\mathcal{L}}_k)=|s|H_k(s)+\eta |s|+O(|\mathrm{\Sigma }{|}^k)$. Эти два важнейших наблюдения показывают, что при использовании A для сжатия каждой подстроки в разбиении, порожденном оптимальным листовым покрытием ${\mathcal{L}}_{min}$, общий размер выходного значения ограничени в терминах $|s|H_k(s)$ для любого $k\ge 0$. На деле $\sum _{u\in {\mathcal{L}}_{min}}{C}_A(\hat{s}⟨u⟩)=C_A({\mathcal{L}}_{min})\le C_A({\mathcal{L}}_k)=|s|H_k(s)+\eta |s|+O(|\mathrm{\Sigma }{|}^k)$.

Суммируя все вышесказанное, усиление алгоритма сжатия A над строкой s состоит из трех основных этапов:

1. Вычислить $\hat{s}=bwt(s)$;

2. Вычислить оптимальное листовое покрытие ${\mathcal{L}}_{min}$ относительно $C_A$ и разбиение $\hat{s}$, соответствующее ${\mathcal{L}}_{min}$;

3. Сжать каждую подстроку разбиения при помощи алгоритма A.

Таким образом, парадигма усиления сводит разработку эффективных алгоритмов сжатия, использующих информацию контексте, к (обычно более простой) разработке алгоритмов сжатия нулевого порядка. Эффективность этой парадигмы описывается следующей теоремой.

Теорема 1 ([Ферраджина и др., 2005). Пусть A – алгоритм сжатия, который сжимает любую строку x до размера не более $|x|H_0(x)+\eta |x|+\mu$ бит. Механизм усиления степени сжатия, примененный к A, дает выходное значение, размер которого ограничен $|s|H_k(s)+log|s|+\eta |s|+O(|\mathrm{\Sigma }{|}^k)$ бит одновременно для всех $k\ge 0$. Учитывая A, механизм усиления привносит в процесс сжатия дополнительные накладные расходы на память в размере O(|s| log |s|) бит, но не вносит дополнительных затрат времени.

Аналогичный результат имеет место и для модифицированной энтропии $H_k^{\ast }$ (однако доказать его намного сложнее): пусть дан алгоритм сжатия A, который сжимает любую строку x до не более чем $\lambda |x|H_0^{\ast }(x)+\mu$ бит. Механизм усиления степени сжатия дает выходное значение, размер которого ограничен $\lambda |s|H_k^{\ast }(s)+log|s|+O(|\mathrm{\Sigma }{|}^k)$ бит одновременно для всех $k\ge 0$. В работе [3] авторы также показали, что ни один алгоритм сжатия, удовлетворяющий некоторым мягким предположениям относительно его внутренних принципов работы, не способен получить схожую границу, не включающую одновременно мультипликативный коэффициент $\lambda$ и аддитивный логарифмический терм. Кроме того, в [3] была предложена конкретизация усилителя, которая сжимает любую строку s до не более чем $2,5|s|H_k^{\ast }(s)+log|s|+O(|\mathrm{\Sigma }{|}^k)$ бит. Эта граница аналитически превосходит границы, доказанные для лучших существующих алгоритмов сжатия, включая алгоритмы Лемпеля-Зива и Барроуза-Уилера и алгоритм PPM.

Применение

Помимо естественного применения в области сжатия данных, механизмы повышения степени сжатия также использовались для разработки сжатых полнотекстовых индексов [8].

Открытые вопросы

Парадигму усиления можно обобщить следующим образом. Пусть дан алгоритм компрессии A; необходимо найти и перестановку $\mathcal{P}$ для символов строки s, и стратегию разбиения, такие, чтобы примененный к ним подход к усилению минимизировал размер выходных данных. Выше были приведены убедительные свидетельства того, что преобразование Барроуза-Уилера является элегантной и эффективной перестановкой $\mathcal{P}$. Как ни удивительно, другие классические задачи сжатия данных также вписываются в эту структуру: поиск кратчайшей общей надстроки (эта задача является MAX-SNP-сложной), кодирование с переменной длиной строки для множества строк (полиномиально разрешимая задача), LZ77 и нахождение минимального количества фраз (также MAX-SNP-сложная). Таким образом, подход к усилению является достаточно общим, чтобы заслуживать дальнейших теоретических и практических исследований [5].

Экспериментальные результаты

Исследование нескольких алгоритмов сжатия, основанных на усилении, и сравнение их с другими современными способами сжатия приведено в работе [ ]. Эксперименты показывают, что техника усиления является более надежной по сравнению с другими подходами и хорошо работает даже с менее эффективными алгоритмами сжатия нулевого порядка. Однако положительные результаты достигаются за счет использования большего количества ресурсов (времени и памяти).

Наборы данных

Наборы данных, использовавшиеся в [ ], доступны по адресу http://www.mfn.unipmn.it/~manzini/boosting. Другие наборы данных для сжатия и индексирования можно найти на сайте Pizza&Chili http://pizzachili.di.unipi.it/.

Ссылка на код

Страница «Усиление алгоритмов сжатия» (Compression Boosting, http://www.mfn.unipmn.it/~manzini/boosting) содержит исходный код всех алгоритмов, протестированных в [ ]. Этот код организован в виде библиотеки с высокой степенью модульности, которая может использоваться любым алгоритмом сжатия и не требует знания алгоритма bwt или процедуры усиления.

См. также

• Арифметическое кодирование для сжатия данных
• Преобразование Барроуза-Уилера
• Индексация сжатого текста
• Сжатие таблиц
• Сжатие и индексирование дерева

Литература

1. Bell, T.C., Cleary, J.G., Witten, I.H.: Text compression. Prentice Hall, NJ (1990)

2. Burrows, M. Wheeler, D.: A block sorting lossless data compression algorithm. Tech. Report 124, Digital Equipment Corporation (1994)

3. Ferragina, P., Giancarlo, R., Manzini, G., Sciortino, M.: Boosting textual compression inoptimal lineartime.J.ACM 52,688-713 (2005)

4. Ferragina, P., Giancarlo, R., Manzini, G.: The engineering of a compression boosting library: Theory vs practice in bwt compression. In: Proc. 14th European Symposium on Algorithms (ESA). LNCS, vol. 4168, pp. 756-767. Springer, Berlin (2006)

5. Giancarlo, R., Restivo, A., Sciortino, M.: From first principles to the Burrows and Wheeler transform and beyond, via combinatorial optimization. Theor. Comput. Sci. 387(3):236-248 (2007)

6. Karp, R., Pippenger, N., Sipser, M.: A Time-Randomness trade-off. In: Proc. Conference on Probabilistic Computational Complexity, AMS, 1985, pp. 150-159

7. Manzini, G.: An analysis of the Burrows-Wheeler transform. J.ACM 48,407-430 (2001)

8. Navarro, G., Makinen, V.: Compressed full text indexes. ACM Comput. Surv.39(1) (2007)

9. Salomon, D.: Data Compression: the Complete Reference, 4th edn. Springer, London (2004)

10. Schapire, R.E.: The strength of weak learnability. Mach. Learn. 2,197-227 (1990)