Связное доминирующее множество: различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| Строка 120: | Строка 120: | ||
Литература | == Литература == | ||
1. Alzoubi, K.M., Wan, P.-J., Frieder, O.: Message-optimal connected dominating sets in mobile ad hoc networks. In: ACM MOBIHOC, Lausanne, Switzerland, 09-11 June 2002 | 1. Alzoubi, K.M., Wan, P.-J., Frieder, O.: Message-optimal connected dominating sets in mobile ad hoc networks. In: ACM MOBIHOC, Lausanne, Switzerland, 09-11 June 2002 | ||
2. Alzoubi, K.M., P.-J.Wan, Frieder, O.: New Distributed Algorithm for Connected Dominating Set in Wireless Ad Hoc Networks. In: HICSS35, Hawaii, January 2002 | 2. Alzoubi, K.M., P.-J.Wan, Frieder, O.: New Distributed Algorithm for Connected Dominating Set in Wireless Ad Hoc Networks. In: HICSS35, Hawaii, January 2002 | ||
3. Ambuhl, C., Erlebach, T., Mihalak, M., Nunkesser, M.: Constant-Factor Approximation for Minimum-Weight (Connected) Dominating Sets in Unit Disk Graphs. In: LNCS, vol.4110, pp 3-14. Springer, Berlin (2006) | 3. Ambuhl, C., Erlebach, T., Mihalak, M., Nunkesser, M.: Constant-Factor Approximation for Minimum-Weight (Connected) Dominating Sets in Unit Disk Graphs. In: LNCS, vol.4110, pp 3-14. Springer, Berlin (2006) | ||
4. Blum, J., Ding, M., Thaeler, A., Cheng, X.: Applications of Connected Dominating Sets in Wireless Networks. In: Du, D.-Z., Pardalos, P. (eds.) Handbook of Combinatorial Optimization, pp. 329-369. Kluwer Academic (2004) | 4. Blum, J., Ding, M., Thaeler, A., Cheng, X.: Applications of Connected Dominating Sets in Wireless Networks. In: Du, D.-Z., Pardalos, P. (eds.) Handbook of Combinatorial Optimization, pp. 329-369. Kluwer Academic (2004) | ||
5. Cheng, X., Huang, X., Li, D., Wu, W., Du, D.-Z.: A polynomial-time approximation scheme for minimum connected dominating set in ad hoc wireless networks. Networks 42,202-208 (2003) | 5. Cheng, X., Huang, X., Li, D., Wu, W., Du, D.-Z.: A polynomial-time approximation scheme for minimum connected dominating set in ad hoc wireless networks. Networks 42,202-208 (2003) | ||
6. Du, D.-Z., Graham, R.L., Pardalos, P.M., Wan, P.-J., Wu, W., Zhao, W.: Analysis of greedy approximations with nonsubmodular potential functions. In: Proceedings of the 19th annual ACM-SIAM Symposium on Discrete Algorithms (SODA) pp. 167-175. January 2008 | 6. Du, D.-Z., Graham, R.L., Pardalos, P.M., Wan, P.-J., Wu, W., Zhao, W.: Analysis of greedy approximations with nonsubmodular potential functions. In: Proceedings of the 19th annual ACM-SIAM Symposium on Discrete Algorithms (SODA) pp. 167-175. January 2008 | ||
7. Dubhashi, D., Mei, A., Panconesi, A., Radhakrishnan, J., Srinivasan, A.: Fast Distributed Algorithms for (Weakly) Connected Dominating Sets and Linear-Size Skeletons. In: SODA, 2003, pp. 717-724 | 7. Dubhashi, D., Mei, A., Panconesi, A., Radhakrishnan, J., Srinivasan, A.: Fast Distributed Algorithms for (Weakly) Connected Dominating Sets and Linear-Size Skeletons. In: SODA, 2003, pp. 717-724 | ||
8. Feige, U.: A Threshold of lnn for Approximating Set Cover. J.ACM 45(4) 634-652 (1998) | 8. Feige, U.: A Threshold of lnn for Approximating Set Cover. J.ACM 45(4) 634-652 (1998) | ||
9. Gfeller, B., Vicari, E.: A Randomized Distributed Algorithm for the Maximal Independent Set Problem in Growth-Bounded Graphs. In: PODC 2007 | 9. Gfeller, B., Vicari, E.: A Randomized Distributed Algorithm for the Maximal Independent Set Problem in Growth-Bounded Graphs. In: PODC 2007 | ||
10. Guha, S., Khuller, S.: Approximation algorithms for connected dominating sets. Algorithmica 20, 374-387 (1998) | 10. Guha, S., Khuller, S.: Approximation algorithms for connected dominating sets. Algorithmica 20, 374-387 (1998) | ||
11. Jia, L., Rajaraman, R., Suel, R.:An Efficient Distributed Algorithm for Constructing Small Dominating Sets. In: PODC, Newport, Rhode Island, USA, August 2001 | 11. Jia, L., Rajaraman, R., Suel, R.:An Efficient Distributed Algorithm for Constructing Small Dominating Sets. In: PODC, Newport, Rhode Island, USA, August 2001 | ||
12. Kuhn, F., Moscibroda, T., Nieberg, T., Wattenhofer, R.: Fast De terministic Distributed Maximal Independent Set Computation on Growth-Bounded Graphs. In: DISC, Cracow, Poland, September 2005 | 12. Kuhn, F., Moscibroda, T., Nieberg, T., Wattenhofer, R.: Fast De terministic Distributed Maximal Independent Set Computation on Growth-Bounded Graphs. In: DISC, Cracow, Poland, September 2005 | ||
13. Kuhn, F., Moscibroda, T., Nieberg,T., Wattenhofer, R.: Local Approximation Schemes for Ad Hoc and Sensor Networks. In: DIALM-POMC, Cologne, Germany, September 2005 | 13. Kuhn, F., Moscibroda, T., Nieberg,T., Wattenhofer, R.: Local Approximation Schemes for Ad Hoc and Sensor Networks. In: DIALM-POMC, Cologne, Germany, September 2005 | ||
14. Kuhn, F., Moscibroda, T., Wattenhofer, R.: On the Locality of Bounded Growth. In: PODC, Las Vegas, Nevada, USA, July 2005 | 14. Kuhn, F., Moscibroda, T., Wattenhofer, R.: On the Locality of Bounded Growth. In: PODC, Las Vegas, Nevada, USA, July 2005 | ||
15. Kuhn, F., Wattenhofer, R.: Constant-Time Distributed Dominating Set Approximation. In: PODC, Boston, Massachusetts, USA, July 2003 | 15. Kuhn, F., Wattenhofer, R.: Constant-Time Distributed Dominating Set Approximation. In: PODC, Boston, Massachusetts, USA, July 2003 | ||
16. Linial, N.: Locality in distributed graph algorithms. SIAM J. Comput. 21(1), 193-201 (1992) | 16. Linial, N.: Locality in distributed graph algorithms. SIAM J. Comput. 21(1), 193-201 (1992) | ||
17. Luby, M.: A Simple Parallel Algorithm for the Maximal Independent Set Problem. SIAM J. Comput. 15,1036-1053 (1986) | 17. Luby, M.: A Simple Parallel Algorithm for the Maximal Independent Set Problem. SIAM J. Comput. 15,1036-1053 (1986) | ||
18. Marathe, M.V., Breu, H., Hunt III, H.B., Ravi, S.S., Rosenkrantz, D.J.: Simple Heuristics for Unit Disk Graphs. Networks 25, 59-68(1995) | 18. Marathe, M.V., Breu, H., Hunt III, H.B., Ravi, S.S., Rosenkrantz, D.J.: Simple Heuristics for Unit Disk Graphs. Networks 25, 59-68(1995) | ||
19. Min, M., Du, H., Jia, X., Huang, X., Huang, C.-H., Wu, W.: Improving construction for connected dominating set with Steiner tree in wireless sensor networks. J. Glob. Optim. 35, 111-119 (2006) | 19. Min, M., Du, H., Jia, X., Huang, X., Huang, C.-H., Wu, W.: Improving construction for connected dominating set with Steiner tree in wireless sensor networks. J. Glob. Optim. 35, 111-119 (2006) | ||
20. Nieberg, T., Hurink, J.L.: A PTAS for the Minimum Dominating Set Problem in Unit Disk Graphs. LNCS, vol. 3879, pp. 296-306. Springer, Berlin (2006) | 20. Nieberg, T., Hurink, J.L.: A PTAS for the Minimum Dominating Set Problem in Unit Disk Graphs. LNCS, vol. 3879, pp. 296-306. Springer, Berlin (2006) | ||
21. Ruan, L., Du, H., Jia, X., Wu, W., Li, Y., Ko, K.-I.: A greedy approximation for minimum connected dominating set. Theor. Comput. Sci. 329, 325-330 (2004) | 21. Ruan, L., Du, H., Jia, X., Wu, W., Li, Y., Ko, K.-I.: A greedy approximation for minimum connected dominating set. Theor. Comput. Sci. 329, 325-330 (2004) | ||
22. Sampathkumar, E., Walikar, H.B.: The Connected Domination Number of a Graph. J. Math. Phys. Sci. 13,607-613 (1979) | 22. Sampathkumar, E., Walikar, H.B.: The Connected Domination Number of a Graph. J. Math. Phys. Sci. 13,607-613 (1979) | ||
23. Thai, M.T., Wang F., Liu, D., Zhu, S., Du, D.-Z.: Connected Dominating Sets in Wireless Networks with Different Transmission Range. IEEE Trans. Mob. Comput. 6(7), 721-730 (2007) | 23. Thai, M.T., Wang F., Liu, D., Zhu, S., Du, D.-Z.: Connected Dominating Sets in Wireless Networks with Different Transmission Range. IEEE Trans. Mob. Comput. 6(7), 721-730 (2007) | ||
24. Wan, P.-J., Alzoubi, K.M., Frieder, O.: Distributed Construction of Connected Dominating Set in Wireless Ad Hoc Networks. In: IEEE INFOCOM 2002 | 24. Wan, P.-J., Alzoubi, K.M., Frieder, O.: Distributed Construction of Connected Dominating Set in Wireless Ad Hoc Networks. In: IEEE INFOCOM 2002 | ||
25. Wu, W., Du, H., Jia, X., Li, Y., Huang, C.-H.: Minimum Connected Dominating Sets and Maximal Independent Sets in Unit Disk Graphs. Theor. Comput. Sci. 352,1 -7 (2006) | 25. Wu, W., Du, H., Jia, X., Li, Y., Huang, C.-H.: Minimum Connected Dominating Sets and Maximal Independent Sets in Unit Disk Graphs. Theor. Comput. Sci. 352,1 -7 (2006) | ||
Версия от 09:04, 23 января 2013
Связное доминирующее множество (Connected_dominating_set)
Ключевые слова и синонимы: техники разбиения
Постановка задачи
Рассмотрим граф G = (V, E). Множество C множества V называется доминирующим множеством, если каждая вершина либо принадлежит к C, либо смежна с вершиной, принадлежащей к C. Если подграф, порожденный С, является связным, то C называется связным доминирующим множеством. Связное доминирующее множество минимальной мощности называется минимальным связным доминирующим множеством (МСДМ). Вычисление МСДМ представляет собой NP-полную задачу, не имеющую аппроксимации с полиномиальным временем исполнения и коэффициентом эффективности [math]\displaystyle{ \rho\ H(\Delta\ ) }[/math] для [math]\displaystyle{ \rho\ \lt 1 }[/math], за исключением случая [math]\displaystyle{ NP \subseteq DTIME(n^{O(lnln n)}) }[/math], где H – гармоническая функция, а [math]\displaystyle{ \Delta\ }[/math] – максимальная степень исходного графа [10].
Единичным диском называется диск с радиусом, равным единице. Граф единичных дисков ассоциирован с множеством единичных дисков на евклидовой плоскости. Каждая вершина является центром единичного диска. Между двумя вершинами u и v существует дуга в том и только том случае, если [math]\displaystyle{ |uv| \le 1 }[/math], где [math]\displaystyle{ |uv| \; }[/math] – евклидово расстояние между u и v. Это означает, что две вершины u и v связаны дугой в том и только том случае, если диск вершины u покрывает v, а диск v покрывает u.
Вычисление МСДМ для графа единичных дисков также является NP-полной задачей; однако можно построить неплохую аппроксимацию для ее решения; Чен и коллеги [5] представили для нее схему аппроксимации с полиномиальным временем исполнения.
История вопроса
Задача нахождения связного доминирующего множества исследовалась в теории графов много лет [22]. В последнее время ее актуальность значительно выросла в связи с применением в области беспроводных сетей, а именно – для построения виртуальных магистралей [4]. Гуха и Хуллер [10] предложили двухступенчатую схему «жадной» аппроксимации для нахождения минимального связного доминирующего множества в графах общего вида и показали, что ее коэффициент эффективности равен [math]\displaystyle{ 3 + ln \Delta\ }[/math], где [math]\displaystyle{ \Delta\ }[/math] – максимальная степень вершины в графе. Построению одноступенчатого жадного алгоритма подобной эффективности мешает трудность нахождения субмодулярной гармонической функции. Руан и коллеги [21] успешно разработали одноступенчатый алгоритм жадной аппроксимации с лучшим коэффициентом эффективности, [math]\displaystyle{ c + ln \Delta\ }[/math], для любого c > 2. Дю и коллеги [6] показали, что существует аппроксимация с полиномиальным временем исполнения и коэффициентом эффективности [math]\displaystyle{ a(1 + ln \Delta\ ) }[/math] для любого [math]\displaystyle{ a \gt 1 \; }[/math]. Важность этих работ заключается в том, что используемые в жадном алгоритме гармонические функции не являются субмодулярными.
Гуха и Хуллер [10] привели доказательство отрицательного результата, заключающегося в следующем: не существует аппроксимации с полиномиальным временем исполнения и коэффициентом эффективности [math]\displaystyle{ \rho\ ln \Delta\ }[/math] для [math]\displaystyle{ \rho\ \lt 1 }[/math], за исключением случая [math]\displaystyle{ NP \subseteq DTIME(n^{O(lnln n)}) }[/math]. Как показано в [8], доминирующие множества не поддаются произвольно качественной аппроксимации, за исключением случаев, когда P почти равно NP. Эти результаты переносят фокус внимания с графов общего вида на графы единичных дисков, поскольку граф единичных дисков представляет собой базовую модель для беспроводных сенсорных сетей, и для графов единичных дисков построение МСДМ имеет аппроксимацию с полиномиальным временем исполнения и константным коэффициентом эффективности. Хотя этот константный коэффициент время от времени удается улучшить [1, 2, 19, 24], Чен и коллеги [5] поставили точку в этом вопросе, доказав существование схемы аппроксимации с полиномиальным временем исполнения (PTAS) для графов единичных дисков. Это значит, что теоретически коэффициент эффективности для алгоритма аппроксимации с полиномиальным временем исполнения может оказаться не выше [math]\displaystyle{ 1 + \varepsilon\ }[/math] для любого положительного [math]\displaystyle{ \varepsilon\ }[/math].
Дубхаши и коллеги [7] показали, что после построения доминирующего множества можно легко вычислить связное доминирующее множество при помощи распределенного алгоритма. Самое полное изложение результатов вычисления доминирующих множеств приведено в [18]. В частности, в этой работе простая константная аппроксимация доминирующих множеств графами единичных дисков. Аппроксимация с константным коэффициентом (связных) доминирующих множеств с минимальными весами для графов единичных дисков была исследована в [3]. Схема аппроксимации с полиномиальным временем исполнения для задачи вычисления минимального доминирующего множества для графов единичных дисков была предложена в [20]. Кун и коллеги [14] доказали, что максимальное независимое множество (и, следовательно, доминирующее множество) можно вычислить за асимптотически оптимальное время O(log n) для графов единичных дисков и крупного класса ограниченных графов независимости. Люби [17] предложил элегантный локальный алгоритм для вычисления максимального независимого множества для графов общего вида с временем исполнения O(log n). Джиа и коллеги [11] предложили быструю распределенную схему аппроксимации для вычисления доминирующего множества для графов общего вида с временем исполнения O(log n). Первый распределенный алгоритм для вычисления доминирующих множеств за константное время с нетривиальным коэффициентом аппроксимации для графов общего вида был приведен в [15]. Соответствующая нижняя граница [math]\displaystyle{ \Omega\ (log n) \; }[/math] считается классическим результатом для распределенного вычисления [16]. Получить схему аппроксимации с полиномиальным временем исполнения для графов единичных дисков можно при помощи распределенного алгоритма [13]. Самый быстрый детерминистский распределенный алгоритм для вычисления доминирующих множеств на графах единичных дисков был приведен в [12], а самый быстрый рандомизированный распределенный алгоритм для них же – в [9].
Основные результаты
Построение схемы аппроксимации с полиномиальным временем исполнения для минимального связного доминирующего множества (МСДМ) базируется на факте существования схемы с полиномиальным временем исполнения и константным коэффициентом эффективности. Этот факт довольно легко обнаружить. Прежде всего, заметим, что единичный диск содержит не более пяти независимых вершин [2]. Из этого следует, что любое максимальное независимое множество имеет размер не более 1 + 4opt, где opt – размер МСДМ. Кроме того, каждое максимальное независимое множество является доминирующим множеством, и можно легко построить максимальное независимое множество с остовным деревом, состоящим из всех дуг длины 2. Все вершины этого остовного дерева образуют связное доминирующее множество размером не более 1 + 8opt. Благодаря улучшению верхней границы размера максимального независимого множества [25] и возможности соединения максимальных независимых множеств [19] значение константного коэффициента было улучшено до 6,8 для распределенного реализации алгоритма.
В этом построении главным образом используются техники неадаптивного разбиения и сдвига. В общем случае ход действий примерно таков: вначале квадрат, содержащий все вершины исходного графа единичных дисков, разделяется на решетку из небольших ячеек. Каждая из этих ячеек далее разбивается на две области – центральную и граничную. Центральная область состоит из точек, находящихся на расстоянии h от границы ячейки. Граничная область состоит из точек, расстояние от которых до границы ячейки составляет не более h + 1. Таким образом, эти области перекрываются. После этого минимальное объединение связных доминирующих множеств вычисляется в каждой ячейке для связных компонент центральной области ячейки. Основная задача состоит в том, чтобы доказать, что объединение всех таких минимальных объединений не превышает минимального связного доминирующего множества для всего графа. Для вершин, не принадлежащих к центральным областям, для вычисления доминирующего множества используется часть 8-аппроксимации, лежащая в граничных областях. Вместе с упоминавшимся ранее объединением она образует связное доминирующее множество для всего исходного графа единичных дисков. Перемещая решетку для получения разбиения по разным координатам, можно получить разбиение с граничной областью, имеющей очень малую верхнюю границу.
Приведем более детальное описание процесса построения.
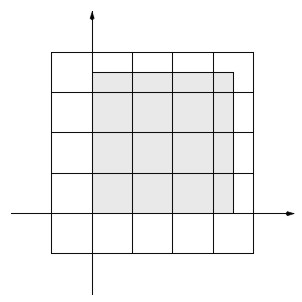
Пусть дан исходный связный граф единичных дисков G = (V, E), располагающийся в квадрате [math]\displaystyle{ Q = \big\{ (x, y) | 0 \le x \le q, 0 \le y \le q \big\}\ }[/math], где [math]\displaystyle{ q \le |V| }[/math]. Для построения приближенного решения с коэффициентом эффективности [math]\displaystyle{ 1 + \varepsilon\ }[/math] для [math]\displaystyle{ \varepsilon\ \gt 0 }[/math] выберем целое число [math]\displaystyle{ m = O((1/ \varepsilon\ )ln(1/ \varepsilon\ )) }[/math]. Пусть [math]\displaystyle{ p = \mathcal{b} q/m \mathcal{c} + 1 }[/math]. Рассмотрим квадрат [math]\displaystyle{ \bar{Q} = \big\{ (x, y) | - m \le x \le mp, - m \le y \le mp \big\} }[/math]. Разобьем [math]\displaystyle{ \bar{Q} }[/math] на [math]\displaystyle{ (p + 1) \times (p + 1) }[/math] решеток таким образом, что каждая ячейка представляет собой квадрат [math]\displaystyle{ m \times m }[/math], за исключением верхней и правой границ; следовательно, никакие две ячейки не перекрываются друг с другом. Обозначим это разбиение квадрата [math]\displaystyle{ \bar{Q} }[/math] как P(0) (см. рис.). В общем случае разбиение P(a) получается из P(0) в результате сдвига нижнего левого угла Q из точки (—m,—m) в точку (—m + a,—m+ a). Заметим, что в результате сдвига из P(0) в P(a) для [math]\displaystyle{ 0 \le a \le m }[/math] квадрат Q оказывается покрыт разбиением.
Квадраты [math]\displaystyle{ Q \; }[/math] и [math]\displaystyle{ \bar{Q} }[/math]
Для каждой ячейки e (представляющей собой квадрат [math]\displaystyle{ m \times m }[/math]) [math]\displaystyle{ C_e(d) \; }[/math] обозначает множество точек в e, удаленных от границы на расстояние не менее d; [math]\displaystyle{ C_e(0) \; }[/math] представляет саму ячейку e. Обозначим [math]\displaystyle{ B_e(d) = C_e(0) - C_e(d) \; }[/math]. Зафиксируем положительное целое число [math]\displaystyle{ h = 7 + 3 \mathcal{b} log_2(4m^2/ \pi\ ) \mathcal{c} }[/math]. Назовем [math]\displaystyle{ C_e(h) \; }[/math] центральной областью ячейки e, а [math]\displaystyle{ B_e(h + 1) \; }[/math] – граничной областью ячейки e. Таким образом, центральная и граничная области каждой ячейки перекрываются на полосу единичной ширины.
Центральная область
Пусть [math]\displaystyle{ G_e(d) \; }[/math] обозначает часть исходного графа G, лежащую в области [math]\displaystyle{ C_e(d) \; }[/math]. Точнее говоря, [math]\displaystyle{ G_e(h) \; }[/math] представляет собой часть графа G, лежащую в центральной области e. [math]\displaystyle{ G_e(h) \; }[/math] может состоять из нескольких связных компонентов. Пусть [math]\displaystyle{ K_e \; }[/math] обозначает подмножество вершин [math]\displaystyle{ G_e(0) \; }[/math] с минимальной мощностью, таких, что для каждого связного компонента H области [math]\displaystyle{ G_e(h),/math подмножество \lt math\gt K_e \; }[/math] содержит связную компоненту, являющуюся доминатором H. Иными словами, [math]\displaystyle{ K_e \; }[/math] представляет собой минимальное объединение связных доминирующих множеств в [math]\displaystyle{ G(0) \; }[/math] для связных компонент [math]\displaystyle{ G_e(h) \; }[/math].
Теперь обозначим за K(a) объединение [math]\displaystyle{ K_e \; }[/math] для e по всем ячейкам разбиения P(a). K(a) обладает двумя важными свойствами.
Лемма 1. K(a) можно вычислить за время [math]\displaystyle{ n^{O(m^2)} \; }[/math].
Лемма 2. [math]\displaystyle{ |K^a| \le opt }[/math] для [math]\displaystyle{ 0 \le a \le m - 1 }[/math].
Справедливость леммы 1 показать несложно. Заметим, что вершины квадрата со сторонами длины [math]\displaystyle{ \sqrt{2}/2 }[/math] порождают полный подграф, в котором каждая вершина доминирует все остальные вершины. Из этого следует, что минимальное доминирующее множество для вершин [math]\displaystyle{ G_e(0) \; }[/math] имеет размер не более [math]\displaystyle{ ( \mathcal{d} \sqrt{2m} \mathcal{e} )^2 }[/math]. Следовательно, размер [math]\displaystyle{ K_e \; }[/math] составляет не более [math]\displaystyle{ 3( \mathcal{d} \sqrt{2m} \mathcal{e} )^2 }[/math], поскольку любое доминирующее множество в связном графе имеет остовное дерево с дугами длиной не более 3. Предположим, что [math]\displaystyle{ G_e(0) \; }[/math] имеет [math]\displaystyle{ n_e \; }[/math] вершин. Тогда количество кандидатов для [math]\displaystyle{ K_e \; }[/math] составляет не более
[math]\displaystyle{ \sum_{k=0}^{3( \mathcal{d} \sqrt{2m} \mathcal{e} )^2} \binom{n_e}{k} = n_e^{O(m^2)} }[/math]
Следовательно, K(a) можно вычислить за время
[math]\displaystyle{ \sum_e n_e^{O(m^2)} \le \bigg( \sum_e n_e \bigg) ^{O(m^2)} = n^{O(m^2)} }[/math]
Доказательство истинности леммы 2 намного сложнее; его можно найти в [5].
Граничная область
Пусть F – связное доминирующее множество G, удовлетворяющее неравенству [math]\displaystyle{ |F| \le 8opt + 1 }[/math]. Обозначим за F(a) подмножество F, лежащее в граничной области [math]\displaystyle{ B_a(h + 1) \; }[/math]. Поскольку построение F занимает полиномиальное время, необходимо рассмотреть только размер F(a).
Лемма 3. Положим [math]\displaystyle{ h = 7 + 3 \mathcal{b} log_2(4m^2/ \pi\ ) \mathcal{c} }[/math] и [math]\displaystyle{ \mathcal{b} m/(h + 1)\mathcal{c} \ge 32/ \varepsilon\ }[/math]. В таком случае имеется по меньшей мере половина [math]\displaystyle{ i = 0; 1, ... , \mathcal{b} m/(h + 1)\mathcal{c} - 1 }[/math], таких, что [math]\displaystyle{ |F(i(h + 1))| \le \varepsilon\ \cdot opt }[/math].
Доказательство. Обозначим за [math]\displaystyle{ F_H(a) \; }[/math] подмножество вершин F(a) с расстоянием менее h + 1 от горизонтальной (и за [math]\displaystyle{ F_V(a) \; }[/math] - соответственно, от вертикальной) границы некоторой ячейки в P(a). Тогда [math]\displaystyle{ F(a) = F_H(a) \cup F_V(a) }[/math]. Более того, все [math]\displaystyle{ F_H(i(h+1)) \; }[/math] для [math]\displaystyle{ i = 0; 1, ... , \mathcal{b} m/(h + 1)\mathcal{c} - 1 }[/math] являются непересекающимися. Следовательно,
[math]\displaystyle{ \sum_{i=0}^{\mathcal{b} m/(h + 1)\mathcal{c} - 1} |F_H(i(h+1))| \le |F| \le 8opt }[/math]
Подобным же образом, все [math]\displaystyle{ F_V(i(h+1)) \; }[/math] для [math]\displaystyle{ i = 0; 1, ... , \mathcal{b} m/(h + 1)\mathcal{c} - 1 }[/math] являются непересекающимися и
[math]\displaystyle{ \sum_{i=0}^{\mathcal{b} m/(h + 1)\mathcal{c} - 1} |F_V(i(h+1))| \le |F| \le 8opt }[/math]
Следовательно,
[math]\displaystyle{ \sum_{i=0}^{\mathcal{b} m/(h + 1)\mathcal{c} - 1} |F(i(h+1))| \le \sum_{i=0}^{\mathcal{b} m/(h + 1)\mathcal{c} - 1} (|F_H(i(h+1))| + |F_V(i(h+1))|) \le 16opt }[/math]
Иначе говоря,
[math]\displaystyle{ \frac {1} {{\mathcal{b} m/(h + 1)\mathcal{c}}} \sum_{i=0}^{\mathcal{b} m/(h + 1)\mathcal{c} - 1} |F(i(h+1))| \le ( \varepsilon\ /2)opt }[/math]
Это означает, что по меньшей мере половина [math]\displaystyle{ F(i(h + 1)) \; }[/math] для [math]\displaystyle{ i = 0; 1, ... , \mathcal{b} m/(h + 1)\mathcal{c} - 1 }[/math] удовлетворяет соотношению[math]\displaystyle{ |F(i(h + 1))| \le \varepsilon\ \cdot opt }[/math]. □
Окончательный результат
Теперь рассмотрим K(a) и F(a). Согласно леммам 2 и 3, существуют [math]\displaystyle{ a \in \big\{ 0, h + 1, ... , (\mathcal{b} m/(h + 1)\mathcal{c} - 1)(h + 1) \big\} }[/math], такие, что
[math]\displaystyle{ |K(a) \cup F(a)| \le (1 + \varepsilon\ )opt }[/math].
Лемма 4. Для [math]\displaystyle{ 0 \le a \le m — 1 }[/math], [math]\displaystyle{ K(a) \cup F(a) }[/math] представляет собой связное доминирующее множество для исходного связного графа G.
Доказательство. Очевидно, что [math]\displaystyle{ K(a) \cup F(a) }[/math] является доминирующим множеством для исходного графа G. Его связность можно показать следующим образом. Заметим, что центральная и граничная области перекрываются на область шириной 1. Таким образом, для любого связного компонента H подграфа [math]\displaystyle{ G_e(h) \; }[/math], у F(a) имеется вершина в H. Следовательно, F(a) должен иметь связь с любым связным доминирующим множеством для H, особенно с [math]\displaystyle{ D_H \; }[/math] в K(a). Это означает, что [math]\displaystyle{ D_H \; }[/math] восстанавливает связи с F, потерянные в результате отрезания части в H. Следовательно, связность [math]\displaystyle{ K(a) \cup F(a) }[/math] следует из связности F. □
Суммируя вышеприведенные положения, получаем следующий результат:
Теорема 1. Существует [math]\displaystyle{ (1 + \varepsilon\ ) }[/math]-аппроксимация для построения минимального связного доминирующего множества в связных графах единичных дисков, время исполнения которой составляет [math]\displaystyle{ n^{O((1/ \varepsilon\ )log(1/ \varepsilon\ )^2)} }[/math].
Применение
Важной областью применения связных доминирующих множеств является построение виртуальных магистралей для беспроводных сетей, особенно для беспроводных сенсорных сетей [4]. Топология беспроводной сенсорной сети часто представляет собой граф единичных дисков.
Открытые вопросы
В общем случае топология беспроводной сенсорной сети представляет собой граф дисков; иначе говоря, каждая вершина ассоциируется с диском. Разные диски могут иметь различный размер. Дуга из вершины u в вершину v существует в том и только том случае, если диск u покрывает v. Виртуальная магистраль в графах дисков представляет собой подмножество вершин, порождающее сильно связный подграф, такой, что каждая вершина, не принадлежащая к подмножеству, имеет входящую дугу из вершины подмножества, а также исходящую дугу, ведущую к вершине подмножества. Такая виртуальная магистраль может рассматриваться как связное доминирующее множество в графе дисков. Вопрос о том, существует ли аппроксимация с полиномиальным временем исполнения и константным коэффициентом эффективности, до сих пор остается открытым. Тай и коллеги [23] достигли в этом отношении определенных успехов.
См. также
- Доминирующее множество
- Точные алгоритмы построения доминирующего множества
- Жадные алгоритмы покрытия множества
- Максимальное листовое остовное дерево
Литература
1. Alzoubi, K.M., Wan, P.-J., Frieder, O.: Message-optimal connected dominating sets in mobile ad hoc networks. In: ACM MOBIHOC, Lausanne, Switzerland, 09-11 June 2002
2. Alzoubi, K.M., P.-J.Wan, Frieder, O.: New Distributed Algorithm for Connected Dominating Set in Wireless Ad Hoc Networks. In: HICSS35, Hawaii, January 2002
3. Ambuhl, C., Erlebach, T., Mihalak, M., Nunkesser, M.: Constant-Factor Approximation for Minimum-Weight (Connected) Dominating Sets in Unit Disk Graphs. In: LNCS, vol.4110, pp 3-14. Springer, Berlin (2006)
4. Blum, J., Ding, M., Thaeler, A., Cheng, X.: Applications of Connected Dominating Sets in Wireless Networks. In: Du, D.-Z., Pardalos, P. (eds.) Handbook of Combinatorial Optimization, pp. 329-369. Kluwer Academic (2004)
5. Cheng, X., Huang, X., Li, D., Wu, W., Du, D.-Z.: A polynomial-time approximation scheme for minimum connected dominating set in ad hoc wireless networks. Networks 42,202-208 (2003)
6. Du, D.-Z., Graham, R.L., Pardalos, P.M., Wan, P.-J., Wu, W., Zhao, W.: Analysis of greedy approximations with nonsubmodular potential functions. In: Proceedings of the 19th annual ACM-SIAM Symposium on Discrete Algorithms (SODA) pp. 167-175. January 2008
7. Dubhashi, D., Mei, A., Panconesi, A., Radhakrishnan, J., Srinivasan, A.: Fast Distributed Algorithms for (Weakly) Connected Dominating Sets and Linear-Size Skeletons. In: SODA, 2003, pp. 717-724
8. Feige, U.: A Threshold of lnn for Approximating Set Cover. J.ACM 45(4) 634-652 (1998)
9. Gfeller, B., Vicari, E.: A Randomized Distributed Algorithm for the Maximal Independent Set Problem in Growth-Bounded Graphs. In: PODC 2007
10. Guha, S., Khuller, S.: Approximation algorithms for connected dominating sets. Algorithmica 20, 374-387 (1998)
11. Jia, L., Rajaraman, R., Suel, R.:An Efficient Distributed Algorithm for Constructing Small Dominating Sets. In: PODC, Newport, Rhode Island, USA, August 2001
12. Kuhn, F., Moscibroda, T., Nieberg, T., Wattenhofer, R.: Fast De terministic Distributed Maximal Independent Set Computation on Growth-Bounded Graphs. In: DISC, Cracow, Poland, September 2005
13. Kuhn, F., Moscibroda, T., Nieberg,T., Wattenhofer, R.: Local Approximation Schemes for Ad Hoc and Sensor Networks. In: DIALM-POMC, Cologne, Germany, September 2005
14. Kuhn, F., Moscibroda, T., Wattenhofer, R.: On the Locality of Bounded Growth. In: PODC, Las Vegas, Nevada, USA, July 2005
15. Kuhn, F., Wattenhofer, R.: Constant-Time Distributed Dominating Set Approximation. In: PODC, Boston, Massachusetts, USA, July 2003
16. Linial, N.: Locality in distributed graph algorithms. SIAM J. Comput. 21(1), 193-201 (1992)
17. Luby, M.: A Simple Parallel Algorithm for the Maximal Independent Set Problem. SIAM J. Comput. 15,1036-1053 (1986)
18. Marathe, M.V., Breu, H., Hunt III, H.B., Ravi, S.S., Rosenkrantz, D.J.: Simple Heuristics for Unit Disk Graphs. Networks 25, 59-68(1995)
19. Min, M., Du, H., Jia, X., Huang, X., Huang, C.-H., Wu, W.: Improving construction for connected dominating set with Steiner tree in wireless sensor networks. J. Glob. Optim. 35, 111-119 (2006)
20. Nieberg, T., Hurink, J.L.: A PTAS for the Minimum Dominating Set Problem in Unit Disk Graphs. LNCS, vol. 3879, pp. 296-306. Springer, Berlin (2006)
21. Ruan, L., Du, H., Jia, X., Wu, W., Li, Y., Ko, K.-I.: A greedy approximation for minimum connected dominating set. Theor. Comput. Sci. 329, 325-330 (2004)
22. Sampathkumar, E., Walikar, H.B.: The Connected Domination Number of a Graph. J. Math. Phys. Sci. 13,607-613 (1979)
23. Thai, M.T., Wang F., Liu, D., Zhu, S., Du, D.-Z.: Connected Dominating Sets in Wireless Networks with Different Transmission Range. IEEE Trans. Mob. Comput. 6(7), 721-730 (2007)
24. Wan, P.-J., Alzoubi, K.M., Frieder, O.: Distributed Construction of Connected Dominating Set in Wireless Ad Hoc Networks. In: IEEE INFOCOM 2002
25. Wu, W., Du, H., Jia, X., Li, Y., Huang, C.-H.: Minimum Connected Dominating Sets and Maximal Independent Sets in Unit Disk Graphs. Theor. Comput. Sci. 352,1 -7 (2006)