Декомпозиция на значительно удаленные пары для графа единичных дисков
Ключевые слова и синонимы
Кластеризация
Постановка задачи
Нотация
Пусть дано конечное множество точек A в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math]. Назовем его ограничивающим прямоугольником R(A) d-мерный гиперпрямоугольник [math]\displaystyle{ [a_1, b_1] \times [a_2, b_2 ] \times ... \times [a_d, b_d] \; }[/math], содержащий A и имеющий минимальную протяженность по каждому измерению.
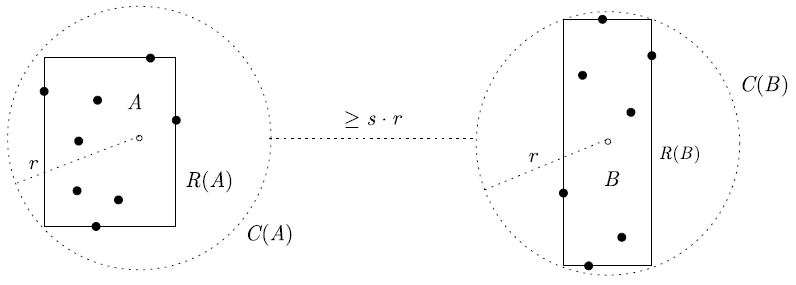
Два множества точек A и B называются значительно удаленными относительно коэффициента удаленности s > 0, если существуют вещественное число r > 0 и две d-мерных сферы [math]\displaystyle{ C_A \; }[/math] и [math]\displaystyle{ C_B \; }[/math] радиуса r каждая, такие, что выполняются следующие соотношения.
1. [math]\displaystyle{ C_A \cap C_B = \empty }[/math]
2. [math]\displaystyle{ C_A \; }[/math] содержит ограничивающий прямоугольник R(A) множества A
3. [math]\displaystyle{ C_B \; }[/math] содержит ограничивающий прямоугольник R(B) множества B
4. [math]\displaystyle{ |C_A C_B| \ge s \cdot r }[/math].
Здесь [math]\displaystyle{ |C_A C_B| \; }[/math] обозначает наименьшее евклидово расстояние между двумя точками в [math]\displaystyle{ C_A \; }[/math] и [math]\displaystyle{ C_B \; }[/math], соответственно. Пример приведен на рис. 1. Пусть даны ограничивающие прямоугольники R(A)и R(B). Для проверки, являются ли множества A и B значительно удаленными относительно s, требуется всего O(d) времени.
Рисунок 1. Множества A и B являются значительно удаленными относительно s
Две точки одного и того же множества, A или B, находятся друг от друга на евклидовом расстоянии, не более чем в 2/s превышающем возможное расстояние между любой парой точек [math]\displaystyle{ (a, b) \in A \times B \; }[/math]. Кроме того, разница расстояний между любыми такими парами (a, b), (a', b'), а именно |a – b|, |a' – b'| не может превышать 1 + 4/s.
Пусть дано множество S из n точек в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math]. Декомпозицией S на значительно удаленные пары относительно коэффициента удаленности s является последовательность пар [math]\displaystyle{ (A_1, B_1), (A_2, B_2), ..., (A_m, B_m) \; }[/math], такая, что
1. [math]\displaystyle{ A_i, B_i \subset S \; }[/math] для i = 1...m
2. [math]\displaystyle{ A_i \; }[/math] и [math]\displaystyle{ B_i \; }[/math] являются значительно удаленными относительно s для i = 1...m
3. Для любых точек [math]\displaystyle{ a, b \in S, a \ne b \; }[/math], существует уникальный индекс i в интервале 1...m, такой, что имеет место либо [math]\displaystyle{ a \in A_i \; }[/math] и [math]\displaystyle{ b \in B_i \; }[/math], либо [math]\displaystyle{ b \in A_i \; }[/math] и a [math]\displaystyle{ \in B_i \; }[/math].
Очевидно, что любое множество [math]\displaystyle{ S = \{ s_1, ..., s_n \} \; }[/math] содержит декомпозицию на значительно удаленные пары. Достаточно просто рассмотреть любые пары одноэлементных множеств [math]\displaystyle{ ( \{ s_i \}, \{ s_j \}) \; }[/math], где i < j. Вопрос заключается в том, существуют ли декомпозиции, состоящие из менее чем [math]\displaystyle{ O(n^2) \; }[/math] пар, и возможно ли их эффективно построить.
Основные результаты
Следующий результат представили Кэллахан и Косарайю [1, 2].
Теорема 1. Пусть даны множество S из n точек в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math] и коэффициент удаленности s, такой, что существует декомпозиция S на значительно удаленные пары относительно s, состоящая из [math]\displaystyle{ O(s^d d^{d/2} n) \; }[/math] пар вида [math]\displaystyle{ (A_i, B_i) \; }[/math]. Она может быть построена за время [math]\displaystyle{ O(d \; n \; log \; n + s^d d^{d/2+1} n) }[/math].
Таким образом, если размерность d и коэффициент удаленности s фиксированы – что имеет место во многих случаях применения – то количество пар составляет O(n), а время вычисления декомпозиции – O(n log n).
Основным инструментом построения декомпозиции на значительно удаленные пары является расщепляемое дерево T(S) множества S. Корень r дерева T(S) содержит ограничивающий прямоугольник R(S) для S. Две его вершины-потомка получаются посредством разделения посередине по наибольшему измерению R(S) при помощи ортогональной гиперплоскости. Она разделяет S на два подмножества [math]\displaystyle{ S_a, S_b \; }[/math], ограничивающие прямоугольники которых [math]\displaystyle{ R(S_a) \; }[/math] и [math]\displaystyle{ R(S_b) \; }[/math] хранятся в двух вершинах-потомках a и b корня r. Процесс повторяется до тех пор, пока в каждом подмножестве не останется только одна точка S. Эти одноэлементные множества образуют листья дерева T(S). Очевидно, что расщепляемое дерево T(S) содержит O(n) вершин. Оно не обязательно должно быть сбалансированным и может быть построено за время O(d n log n).
Декомпозицию S на значительно удаленные пары относительно заданного коэффициента удаленности s теперь можно получить из T(S) следующим образом. Для каждой внутренней вершины T(S) с потомками v и w вызывается следующая рекурсивная процедура FindPairs(v, w). Если [math]\displaystyle{ S_v \; }[/math] и [math]\displaystyle{ S_w \; }[/math] являются значительно удаленными, то процедура выдает результат [math]\displaystyle{ (S_v, S_w) \; }[/math]. В противном случае предположим, что наибольшее измерение [math]\displaystyle{ R(S_v) \; }[/math] превышает по длине наибольшее измерение [math]\displaystyle{ R(S_w) \; }[/math] и что [math]\displaystyle{ v_l, v_r \; }[/math] являются вершинами-потомками v в дереве T(S). После этого вызываются процедуры FindPairs([math]\displaystyle{ v_l }[/math], w) и FindPairs([math]\displaystyle{ v_r }[/math], w).
Общее количество вызовов процедуры ограничено количеством найденных значительно удаленных пар, которое, согласно соображению об упаковке, составляет [math]\displaystyle{ O(s^d d^{d/2} n) \; }[/math]. Однако совокупный размер всех множеств [math]\displaystyle{ A_i, B_i \; }[/math] в декомпозиции в общем случае является квадратичным относительно n.
Применение
Далее размерность d будет считаться константной. Декомпозиция на значительно удаленные пары может эффективно применяться для решения задач о близости на точках в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math].
Теорема 2. Пусть S – множество из n точек в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math]. Тогда пара ближайших точек в S может быть найдена за оптимальное время O(n log n).
И в самом деле, пусть [math]\displaystyle{ q \in S \; }[/math] – ближайший сосед точки [math]\displaystyle{ p \in S \; }[/math]. Можно построить декомпозицию S на значительно удаленные пары относительно коэффициента удаленности s > 2 за время O(n log n). Пусть [math]\displaystyle{ (A_i, B_i) \; }[/math] – пара, в которой [math]\displaystyle{ p \in A_i \; }[/math] и [math]\displaystyle{ q \in B_i \; }[/math]. Если бы в [math]\displaystyle{ A_i \; }[/math] имелась другая точка [math]\displaystyle{ p' \; }[/math] из множества S, имело бы место соотношение [math]\displaystyle{ |pp'| \le 2/s \cdot |pq| \lt |pq| }[/math], что невозможно. Следовательно, [math]\displaystyle{ A_i \; }[/math] является одноэлементным множеством. Если (p, q) является парой ближайших точек в S, то множество [math]\displaystyle{ B_i \; }[/math] тоже должно быть одноэлементным. Таким образом, пару ближайших точек можно найти путем рассмотрения всех пар одноэлементных множеств среди O(n) пар, входящих в декомпозицию на значительно удаленные пары.
При помощи следующих действий можно получить более общий результат.
Теорема 3. Пусть S – множество из n точек в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math], и пусть [math]\displaystyle{ k \le n \; }[/math]. Тогда для каждой точки [math]\displaystyle{ p \in S \; }[/math] можно вычислить k ее ближайших соседей в S за совокупное время O(n log n + nk). В частности, для каждой точки S ее ближайшего соседа по S можно найти за оптимальное время O(n log n).
В случае размерности d = 2 для решения этих задач обычно используется диаграмма Вороного. Но для более высоких размерностей намного практичнее использовать декомпозицию на значительно удаленные пары, поскольку сложность диаграммы Вороного для n точек может достигать [math]\displaystyle{ n^{\lfloor d/2 \rfloor} \; }[/math].
Основным способом применения декомпозиции на значительно удаленные пары является построение достаточно хороших остовов для заданного множества точек S. Остовом S с протяженностью t является геометрическая сеть N с множеством вершин S, такая, что для любых двух вершин [math]\displaystyle{ p, q \in S \; }[/math] евклидова длина кратчайшего пути, соединяющего p и q в N, не более чем в t раз превышает евклидово расстояние |pq|.
Теорема 4. Пусть S – множество из n точек в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math], и пусть t > 1. Тогда остов S с протяженностью t, содержащий [math]\displaystyle{ O(s^d n) \; }[/math] ребер, можно построить за время [math]\displaystyle{ O(s^dn + n \; log \; n) }[/math], где s = 4(t + 1)(t - 1).
И в самом деле, если выбрать одно ребро [math]\displaystyle{ (a_i, b_i) \; }[/math] из каждой пары [math]\displaystyle{ (A_i, B_i) \; }[/math] декомпозиции S на значительно удаленные пары относительно s, то эти ребра формируют t-остов S, что можно показать по индукции по рангу каждой пары [math]\displaystyle{ (p, q) \in S^2 \; }[/math] в списке всех таких пар, отсортированном по расстоянию.
Остовы сами по себе имеют немало любопытных областей применения.
Открытые вопросы
Остается открытым важный вопрос: в каких метрических пространствах допускается существование декомпозиций на значительно удаленные пары. Легко увидеть, что соображение об упаковке, использовавшееся для случая евклидова расстояния, можно распространить на случай с выпуклыми функциями расстояния в [math]\displaystyle{ \mathbb{R}^d }[/math]. Рассматривая более общую перспективу, Талвар [6] показал, как вычислять декомпозиции на значительно удаленные пары для множеств точек с ограниченными пропорциями в метрических пространствах с ограниченным дублирующим измерением.
С другой стороны, для метрики, порожденной графом дисков в пространстве [math]\displaystyle{ \mathbb{R}^2 }[/math], декомпозиция на значительно удаленные пары может потребовать квадратичного количества пар. (В графе дисков каждая точка [math]\displaystyle{ p \in S \; }[/math] является центром диска [math]\displaystyle{ D_p \; }[/math] радиуса [math]\displaystyle{ r_p \; }[/math]. Две точки [math]\displaystyle{ p, q \; }[/math] связаны ребром в том и только том случае, если [math]\displaystyle{ D_p \cap D_q \ne \empty }[/math]. Эта метрика определяется евклидовой длиной кратчайшего пути в полученном графе. Если граф представляет собой звезду с лучами идентичной длины, декомпозиция на значительно удаленные пары относительно коэффициента s > 4 должна состоять из пар одноэлементных множеств). Гао и Чжан [4] показали, что даже при использовании графа единичных дисков может потребоваться [math]\displaystyle{ \Omega(n^{2 - 2/d}) \; }[/math] пар для точек в пространстве [math]\displaystyle{ \mathbb{R}^d }[/math].
См. также
Литература
1. Callahan, P.: Dealing with Higher Dimensions: The Well-Separated Pair Decomposition and Its Applications. Ph.D. Thesis, The Johns Hopkins University, USA (1995)
2. Callahan, P.B., Kosaraju, S.R.: A Decomposition of Multidimensional Point Sets with Applications to k-Nearest Neighbors and n-Body Potential Fields. J. ACM 42(1), 67-90 (1995)
3. Eppstein, D.: Spanning Trees and Spanners. In: Sack, J.R., Urrutia, J. (eds.) Handbook of Computational Geometry, pp. 425-461. Elsevier, Amsterdam (1999)
4. Ghao, J., Zhang, L.: Well-Separated Pair Decomposition for the Unit Disk Graph Metric and its Applications. SIAM J. Comput. 35(1),151-169(2005)
5. Narasimhan, G., Smid, M.: Geometric Spanner Networks. Cambridge University Press, New York (2007)
6. Talwar, K.: Bypassing the Embedding: Approximation Schemes and Compact Representations for Low Dimensional Metrics. In: Proceedings of the thirty-sixth Annual ACM Symposium on Theory of Computing (STOC'04), pp. 281-290 (2004)