BB-Дерево
Материал из WikiGrapp
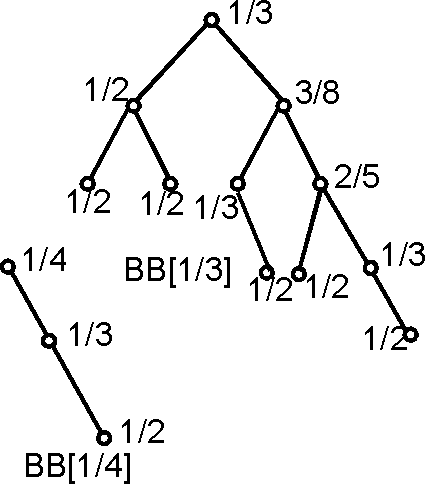
[math]\displaystyle{ BB }[/math]-Дерево ([math]\displaystyle{ BB }[/math]-Tree) — дерево [math]\displaystyle{ T_{n} \, = \, (T_{l}, r, T_{r}) }[/math] с корнем [math]\displaystyle{ r }[/math] называется [math]\displaystyle{ BB }[/math]-деревом с балансом [math]\displaystyle{ \alpha }[/math], [math]\displaystyle{ 0 \leq \alpha \leq 1/2 }[/math], если:
а) для корневого баланса [math]\displaystyle{ \rho(T_{n}) }[/math] выполняется условие [math]\displaystyle{ \alpha \leq \rho(T_{n}) \leq 1-\alpha }[/math];
б) [math]\displaystyle{ T_{l} }[/math] и [math]\displaystyle{ T_{r} }[/math] — [math]\displaystyle{ BB }[/math]-деревья с балансом [math]\displaystyle{ \alpha }[/math].
Другое название — Балансированное по весу дерево.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980.