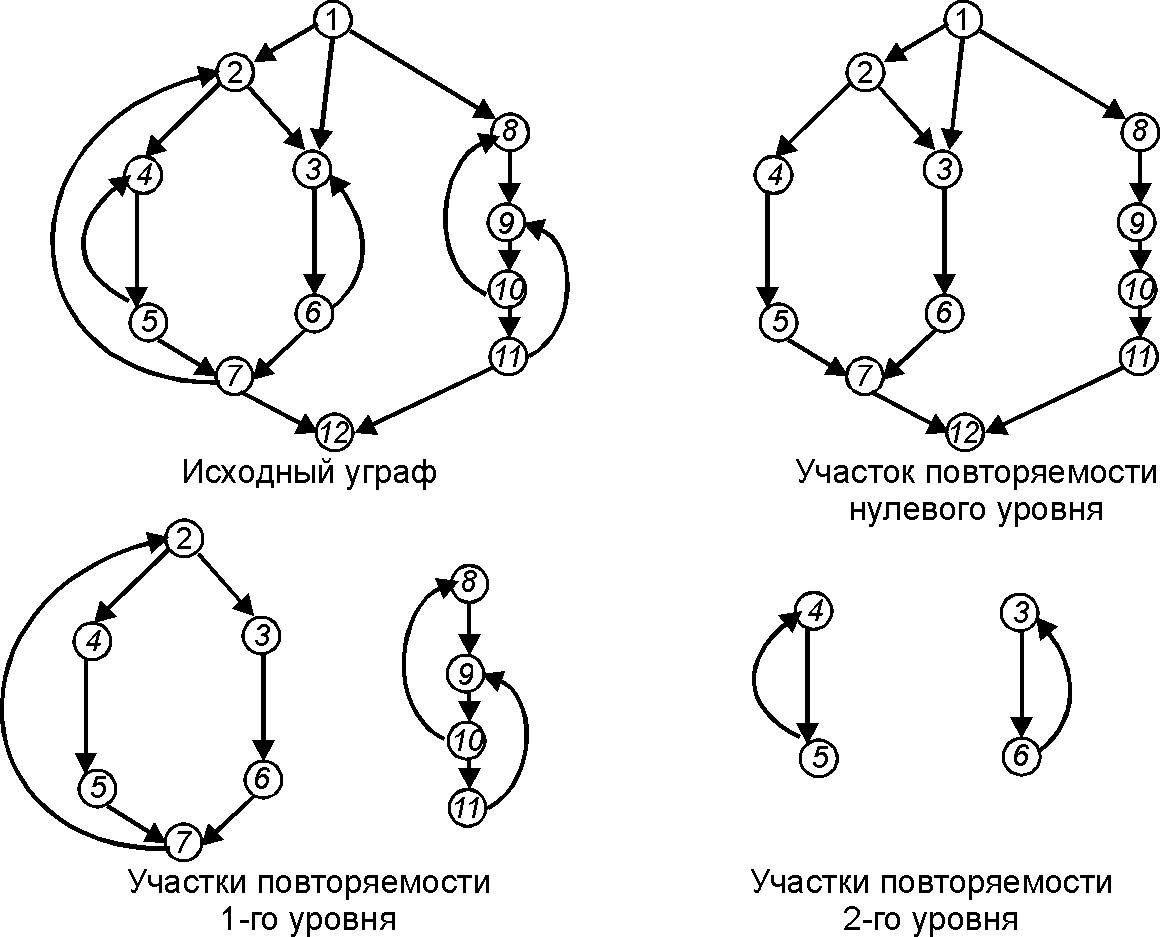
Участок повторяемости
Участок повторяемости (Repeatedly executed region) — конструкция, позволяющая на основе анализа уграфа эффективно выявлять циклическую структуру алгоритма и находить отношения частот выполнения между всеми подмножествами его элементов, которые не противоречат достоверным отношениям частот выполнения.
Пусть [math]\displaystyle{ \,G }[/math] — некоторый уграф с начальной вершиной [math]\displaystyle{ \,p_0 }[/math] и конечной [math]\displaystyle{ \,q_0 }[/math], [math]\displaystyle{ \,V }[/math] — множество всех простых путей по [math]\displaystyle{ \,G }[/math] от [math]\displaystyle{ \,p_0 }[/math] до [math]\displaystyle{ \,q_0 }[/math], а [math]\displaystyle{ \,W }[/math] — множество всех ее простых контуров.
Элементы множества [math]\displaystyle{ E=V \cup W }[/math] называются цепочками уграфа [math]\displaystyle{ \,G }[/math]: простыми, если они принадлежат [math]\displaystyle{ \,V }[/math], и замкнутыми, если они содержатся в [math]\displaystyle{ \,W }[/math]. Говорят, что замкнутая цепочка [math]\displaystyle{ \,P_1 }[/math] вложена в замкнутую цепочку [math]\displaystyle{ \,P_2 }[/math], если [math]\displaystyle{ \,P_2 }[/math] содержит все вершины и все дуги цепочки [math]\displaystyle{ \,P_1 }[/math], за исключением одной дуги. [math]\displaystyle{ \,P_1 }[/math] непосредственно вложена в замкнутую цепочку [math]\displaystyle{ \,P_2 }[/math], если [math]\displaystyle{ \,P_1 }[/math] вложена в [math]\displaystyle{ \,P_2 }[/math] и не существует такой замкнутой цепочки [math]\displaystyle{ \,P_3 }[/math], что
[math]\displaystyle{ \,P_1 }[/math] вложена в [math]\displaystyle{ \,P_3 }[/math], а [math]\displaystyle{ \,P_3 }[/math] вложена в [math]\displaystyle{ \,P_2 }[/math]. Цепочка [math]\displaystyle{ \,P \in W }[/math] называется внешней, если в [math]\displaystyle{ \,W }[/math] не существует такой цепочки, в которую [math]\displaystyle{ \,P }[/math] вложена. Множество цепочек [math]\displaystyle{ \,C }[/math] называется зацепленными, если оно состоит из попарно не вложенных замкнутых цепочек и граф, образованный всеми теми вершинами и дугами, которые принадлежат цепочкам из
[math]\displaystyle{ \,C }[/math], является сильно связным. Пусть [math]\displaystyle{ \,C_1 }[/math] и [math]\displaystyle{ \,C_2 }[/math] — два
зацепленных множества замкнутых цепочек схемы [math]\displaystyle{ G;\, C_1 }[/math] (непосредственно) вложено в [math]\displaystyle{ \,C_2 }[/math], если пересечение [math]\displaystyle{ \,C_1 }[/math] и [math]\displaystyle{ \,C_2 }[/math] пусто и для любой цепочки из [math]\displaystyle{ \,C_1 }[/math] найдется цепочка в [math]\displaystyle{ \,C_2 }[/math], в которую она (непосредственно) вложена.
Участок повторяемости уграфа [math]\displaystyle{ \,G }[/math] определяются следующим образом:
1) [math]\displaystyle{ \,G }[/math] содержит единственный участок повторяемости нулевого уровня, состоящий из всех простых цепочек [math]\displaystyle{ \,V }[/math];
2) участки повторяемости первого уровня [math]\displaystyle{ \,G }[/math] — это максимальные зацепленные множества его внешних замкнутых цепочек;
3) участком повторяемости [math]\displaystyle{ \,i }[/math]-го уровня, [math]\displaystyle{ \,i\gt 1 }[/math], является каждое максимальное зацепленное множество замкнутых цепочек, непосредственно вложенных в некоторый участок повторяемости ([math]\displaystyle{ \,i-1 }[/math])-го уровня.
См. также
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.