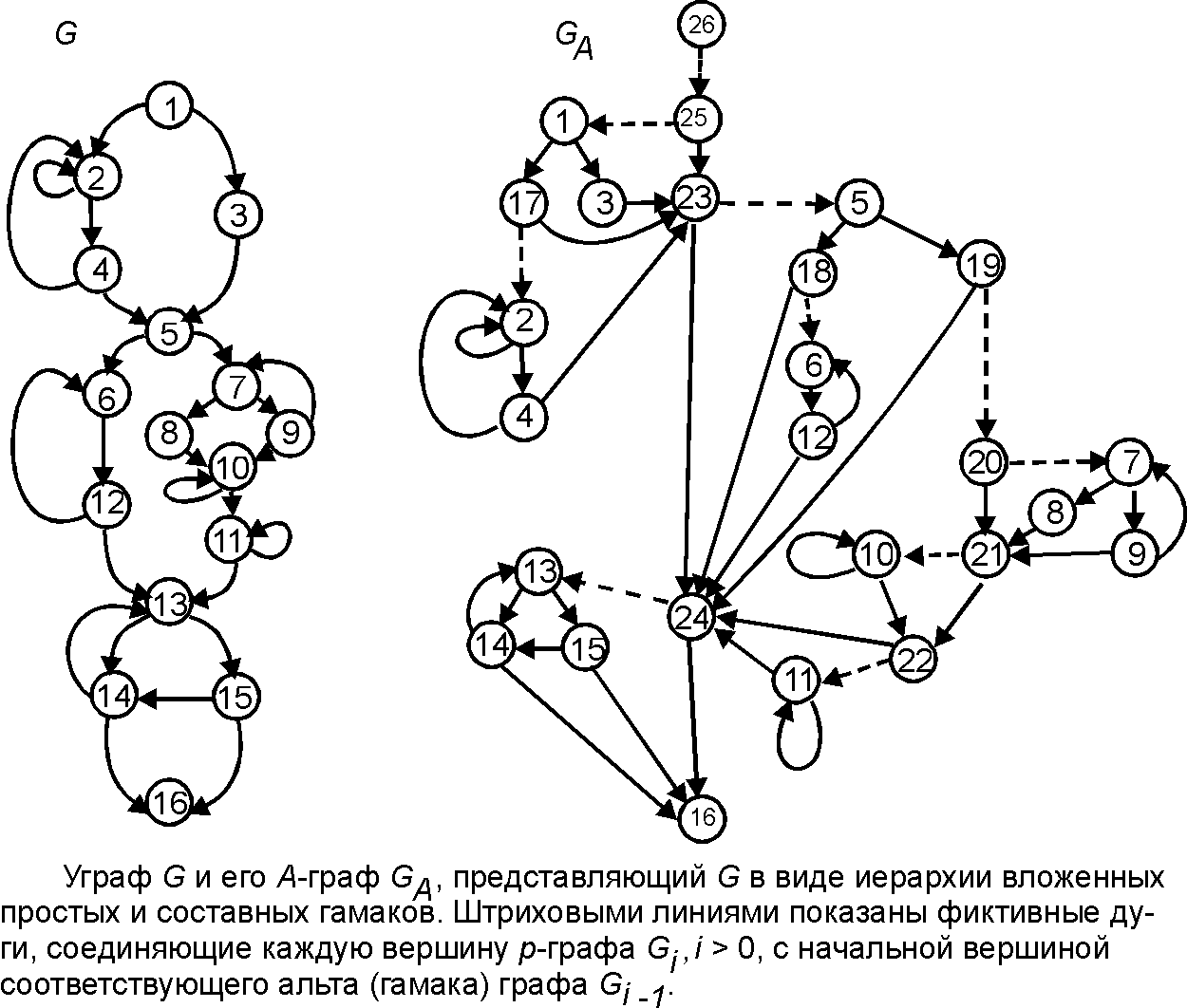
Иерархия вложенных альтов

Иерархия вложенных альтов (Hierarchy of nested alts) — множество нетривиальных альтов $\,A = \{H_{i}\}$ управляющего графа таких, что для любых двух альтов либо их пересечение пусто, либо один целиком содержится в другом.

Альт $H_{i} \in A$ непосредственно вложен в альт $H_{j} \in A$ относительно $\,A$ , если $H_{i} \subset H_{j}$ и в $\,A$ не существует такого альта $\,H_{k}$ , что $H_{i} \subset H_{k} \subset H_{j}$ .

Альт $H_{i} \in A$ называется внутренним альтом относительно $\,A$ , если в $\,A$ не существует альтов, непосредственно вложенных в $\,H_{i}$ и внешним альтом относительно $\,A$ , если в $\,A$ не существует альта, в который $\,H_{i}$ непосредственно вложен.

Последовательность уграфов $G_{0}, \; G_{1}, \; \ldots, \; G_{r}$ называется представлением уграфа $\,G$ в виде иерархии вложенных альтов $\,A$ (A-граф, A-представление уграфа $\,G$ ), если

$\,G_{0} = G$ ,

$\,G_{r}$ — тривиальный уграф и

для любого $\,i$ уграф $\,G_{i}$ получается из $\,G_{i-1}$ стягиванием в вершины всех внешних альтов относительно $\bigcup \{A_{j} : \; 1 \leq j \leq i \}$ , где $\,A_{j}$ — множество всех внутренних альтов относительно $A\setminus \bigcup \{A_{s}: \; 1 \leq s < j\}$ .