nextupprevious

Next:4.6 Обходы графа в глубину и ширину
Up:4 Разработка алгоритмов
Previous:4.4 Алгоритм поиска с возвращением

4.5 Обходы ордерева в глубину и в ширину

Во многих задачах необходимо обойти некоторое ордерево в глубину или в ширину (см. раздел. 2.1), посещая каждую его вершину в точности один раз и выполняя при этом некоторую систематическую обработку информации, относящейся к этой вершине. Посещение каждой вершины дерева может быть связано или с выполнением простой операции, например с распечаткой пометки вершины дерева, или со сложной, например с вычислением некоторой функции.

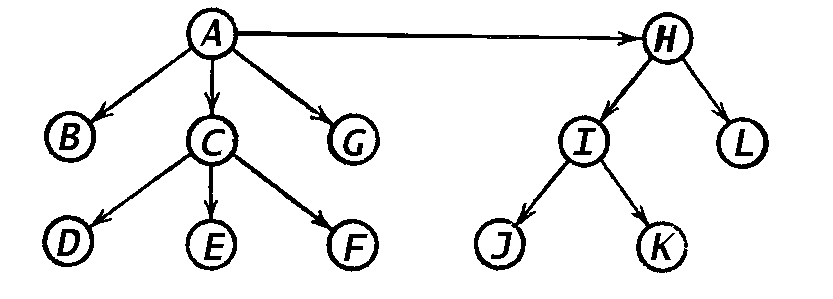
Рис. 20. Дерево

Существует три способа обхода ордерева в глубину, различающихся порядком посещения вершины и ее сыновей При префиксном обходе ордерева $T$, сначала нужно посетить его корень $v$, а затем, если $v$ не является листом, то для реализовать префиксный обход всех ее поддеревьев в порядке их упорядоченности. Например, для дерева, показанного на рис. 20, вершины будут проходиться в следующем порядке: $A,B,C,D,E,F,G,H,I,J,K,L$. Следующая рекурсивная процедура реализует префиксный обход ордерева:

procedure ПРЕФИКСНЫЙ-ОБХОД($T$: ордерево);
begin
    Посетить корень $v$ ордерева $T$;
    if$v$ не лист then
        Пусть $T_1,\ldots,T_k$ -- поддеревья корня $v$;
        for i := 1 to k do ПРЕФИКСНЫЙ-ОБХОД($T_i$) end
    end
end.

Если использовать стек $S$ для хранения текущего пути по дереву, т.е. пути, который начинается в корне дерева и кончается в вершине, посещаемой в данный момент, то можно предложить следующий нерекурсивный алгоритм префиксного обхода ордерева:

Посетить корень дерева и поместить его в пустой стек $S$;
while стек $S$ не является пустым do
    Пусть $p$ -- вершина, находящаяся на верху стека $S$;
    if Сыновья вершины $p$ еще не посещались
    then Посетить старшего сына вершины $p$ и поместить его в стек $S$
    else
           Удалить вершину $p$ из стека S;
            if$p$ имеет братьев then Посетить брата вершины $p$ и поместить его в стек $S$end
    end
end

Аналогичные алгоритмы можно использовать для двух других способа обхода ордерева в глубину: постфиксного и инфиксного.

Способ обхода ордерева в ширину предполагает посещение вершин ордерева по старшинству, уровень за уровнем, отправляясь от корня. Например, при обходе в ширину изображенного на рис. 20 дерева вершины проходятся сверху вниз и слева направо и посещаются в следующем порядке: $A,B,C,G,H,D,E,F,I,L,J,K$. Приведенный ниже алгоритм реализует обход дерева в ширину, используя очередь О.

Поместить корень в пустую очередь O;
while очередь O не пуста do
        Пусть $p$ -- первая вершина очереди O;
        Посетить вершину $p$ и удалить ее из O;
        Поместить всех сыновей вершины $p$ в очередь O, начиная со старшего сына
end
 

Следует заметить, что обход дерева поиска в ширину позволяет обходить дерево поиска одновременно с его построением. Таким образом, можно решать задачу нахождения какого-нибудь одного решения в форме вектора $(a_1,a_2,\ldots)$ неизвестной длины (не зная $r$), если только известно, что существует конечное решение задачи.

Next:4.6 Обходы графа в глубину и ширину
Up:4 Разработка алгоритмов
Previous:4.4 Алгоритм поиска с возвращением

© В.Н. Касьянов, Е.В.Касьянова,2004