2.3 Формулы и программы

Next:2.4 Геометрия
Up:2 Словарь понятий, используемых в заданиях
Previous:2.2 Грамматики, языки и автоматы

2.3 Формулы и программы

Логической переменной называют такую переменную, которая может принимать только два логических значения, обозначаемых здесь, как и в языке Zonnon,

Логическая функция $f(x_1, \ldots, x_n)$ осуществляет отображение $f: \{FALSE,TRUE\}^n \rightarrow \{FALSE, TRUE\}$ . Вот пример логической функции, заданной таблично:

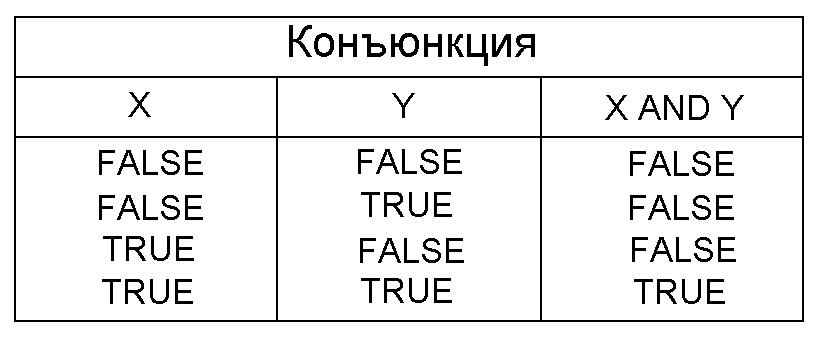
Другой способ задания логических функций -- это запись логических формул. Язык записи логических формул мы опишем с помощью грамматики.

логическая-формула::= { конъюнкция | конъюнкция OR пробелы логическая-формула}

конъюнкция::= { множитель | множитель AND пробелы конъюнкция}

множитель::={NOT пробелы множитель | переменная | (логическая-формула) |TRUE пробелы |FALSE пробелы}

переменная::= {буква | пробелы}

пробелы::={ символ-пробела | символ-пробела пробелы}

Смысл логических формул в точности соответствует их смыслу как логических выражений языка Паскаль. Заметим лишь, что в логических формулах в отличие от логических выражений Паскаля в качестве переменных мы допускаем для простоты только однобуквенные идентификаторы. Например, значениями логических формул $X\ AND\ Y\ OR\ Y$ и $X\ AND\ (Y\ OR\ Y)$ для заданных значений и будут и соответственно.

Две логические формулы называются эквивалентными, если для любого набора значений входящих в них переменных их значения совпадают, т.е. если они задают одну и ту же логическую функцию.

Например, логическая формула эквивалентна каждой из трех логических формул

$NOT\ FALSE$ , $TRUE\ OR\ FALSE$ и $X\ OR\ NOT\ X$ .

Через $\tilde {\alpha}$ будем обозначать логическую формулу, получающуюся из логической формулы $\alpha$ заменой на один символ пробела всякой максимальной серии пробелов в $\alpha$ .

Логическая формула $\beta$ называется вхождением в логическую формулу $\alpha$ (или ее подформулой), если выполнено хотя бы одно из следующих условий:

а) $\tilde{\alpha} = \tilde{\beta}$ ;
б) $\tilde{\alpha} = \sigma\ OR\ \tau$ , где $\sigma$ -- конъюнкция, а $\tau$ -- логическая формула, причем $\beta$ -- подформула одной из формул $\sigma$ или $\tau$ ;
в) $\tilde{\alpha} = \sigma \ AND\ \tau$ , где $\sigma$ -- множитель, а $\tau$ -- конъюнкция, причем $\beta$ -- подформула одной из формул $\sigma$ или $\tau$ ;

г) $\alpha = (\sigma)$ , а $\beta$ -- подформула формулы $\sigma$ ;
д) $\tilde{\alpha} = NOT\ \sigma$ , где $\sigma$ -- множитель, а формула $\beta$ является подформулой множителя $\sigma$ .

Например, формула $X\ AND\ Y$ -- подформула формулы $\sigma = X\ AND\ Y\ OR\ Z$ , а формула $Y\ OR\ Z$ -- нет, поскольку не является конъюнкцией.

Еще один способ задания логических функций -- это их запись в виде так называемых дизъюнктивных нормальных форм (ДНФ). Язык ДНФ мы снова опишем с помощью грамматики.

ДНФ::={FALSE пробелы | элементарная-конъюнкция | элементарная-конъюнкция OR пробелы ДНФ}

элементарная-конъюнкция::= {литерал | литерал элементарная-конъюнкция}

литерал::={переменная | NOT пробелы переменная}

переменная::= буква пробелы

пробелы::={символ-пробела | символ-пробела пробелы}

Например, $X\ OR\ NOT\ X\ Y$ и $X\ Y\ Z$ -- дизъюнктивные нормальные формы, задающие соответственно логические формулы $X\ OR\ NOT\ X\ AND\ Y$ и $X\ AND\ Y\ AND\ Z$ .

Вообще, чтобы по ДНФ построить формулу, задающую ту же логическую функцию, нужно между всякими двумя следующими друг за другом литералами вставить символ операции .

ДНФ называется правильной, если для каждой ее элементарной конъюнкции выполнено следующее условие: все буквы переменных, встречающиеся в этой элементарной конъюнкции, различны. Например, $X\ Y$ -- правильная ДНФ, а $X\ NOT\ X$ -- хоть и ДНФ, но не правильная.

Правильная ДНФ $\alpha$ называется совершенной дизъюнктивной нормальной формой (СДНФ), если каждая максимальная элементарная конъюнкция в $\alpha$ содержит вхождения всех переменных ДНФ $\alpha$ .

Дадим определение расширенной (логической) формулы, дополняя определение логической формулы синтаксическим правилом:

расширенная-формула::= {логическая-формула | логическая-формула {| }расширенная-формула}

и заменяя определение множителя на правило

множитель::=
{NOT пробелы множитель | TRUE пробелы | FALSE пробелы | переменная пробелы | (расширенная-формула)}

Таким образом, логические операции $\rightarrow$ и $\equiv$ имеют меньший приоритет, чем каждая из операций NOT, AND и OR, т.е. при отсутствии скобок они выполняются в последнюю очередь. Правила вычисления этих операций:

$(\alpha \rightarrow \beta) = (\neg \alpha \vee \beta)\mbox{ и } (\alpha \equiv \beta)=(\alpha \& \beta)\vee (\neg\alpha \& \neg \beta).$

Правилом преобразования логических формул называется всякая пара $\phi \Rightarrow \psi$ , где $\phi,\psi$ -- логические формулы.

Применение правила $\phi \Rightarrow \psi$ к логической формуле $\alpha$ состоит в том, что в $\alpha$ выделяется вхождение формулы $\phi$ и заменяется на формулу $\psi$ . Если $\alpha$ не содержит подформул $\phi$ , то говорят, что правило $\phi \Rightarrow \psi$ неприменимо к формуле $\alpha$ .

Упрощением логической формулы $\alpha$ относительно заданного множества правил называется формула $\alpha'$ , которая получается из $\alpha$ многократным применением правил из до тех пор, пока в имеется хотя бы одно правило, применимое к результату предыдущих применений правил.

Для записи бесконечных множеств правил в формулировках заданий используются схемы правил. В схемах правил вместо переменных записываются (возможно, промежуточные) названия соответствующих синтаксических понятий: логическая формула, конъюнкция, множитель, переменная. Тогда, например, схема правил

множитель AND множитель => множитель

означает бесконечное множество правил, получающихся из этой схемы одновременной заменой множителя на какой-нибудь конкретный множитель, т.е. это множество правил будет содержать, в частности, правила

$TRUE\ AND\ TRUE \Rightarrow TRUE$ ,
$X\ AND\ X \Rightarrow X$ ,
$(X\ OR\ Y) AND (X\ OR\ Y) \Rightarrow (X\ OR\ Y)$ .

Логический фрагмент $\Phi$ над алфавитом логических переменных $X= \{ x_1,\ldots, x_n \}$ задается конечным множеством вершин, из каждой вершины выходят либо две дуги, помеченные символами "+" и "-" (плюс- и минус-стрелка соответственно), либо ни одной (такие вершины называются висячими). Всякая висячая вершина помечена числом из $\{0,1,\ldots,9 \}$ , а всякая невисячая вершина -- символом из . Символ, помечающий невисячую вершину, называют ее условием. Одна из вершин фрагмента выделена как начальная.

Если фиксировано некоторое распределение $I:X \rightarrow \{FALSE,TRUE\}$ значений истинности логических переменных из , то тем самым задан и путь $\omega_I$ от начальной вершины фрагмента $\Phi$ , определяемый по правилу: если условие вершины истинно при , то путь продолжается по плюс-стрелке этой вершины, в противном случае -- по минус-стрелке.

Два логических фрагмента эквивалентны, если при любом распределении значений истинности логических переменных пути $\omega^1_I$ и $\omega^2_I$ в первом и втором логических фрагментах либо одновременно бесконечны, либо кончаются висячими вершинами с одинаковыми пометками.

Например, логические фрагменты и на рис. 12 эквивалентны.

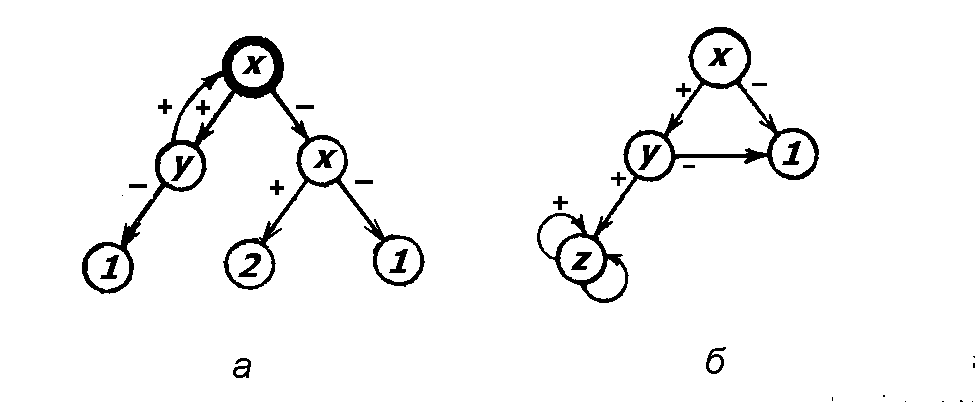
Рис. 12. Примеры логических фрагментов: (а) и (б)

Логический фрагмент $\Phi$ называется свободным, если всякий конечный путь от начала в $\Phi$ задается некоторым распределением значений истинности переменных из . В примере на рис. 8.12 фрагмент свободен, а -- нет.

Логический фрагмент тотален, если при любом распределении путь $\omega_I$ конечен, т.е. ведет от начальной к одной из висячих вершин.

Логический фрагмент пуст, если при любом путь $\omega_I$ бесконечен.

На рис. 13 приведены примеры пустого и тотального логических фрагментов.

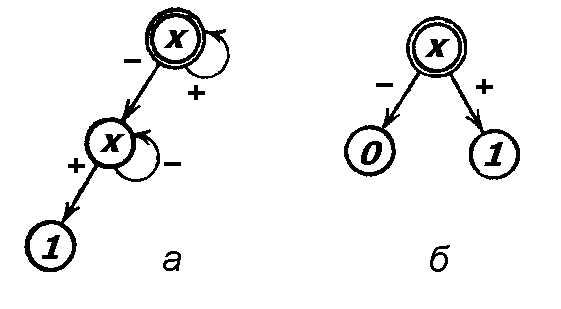
Рис. 13. Пример пустого (а) и тотального (б) логических фрагментов

Если каждая из висячих вершин тотального логического фрагмента $\Phi$ помечена одним из двух чисел 0 или 1, то такой фрагмент задает логическую функцию $f_{\Phi}$ от переменных из . Mы полагаем $f_{\Phi}(I(x_1),\ldots,I(x_n))=TRUE$ тогда и только тогда, когда $\omega_I$ кончается висячей вершиной с пометкой 1.

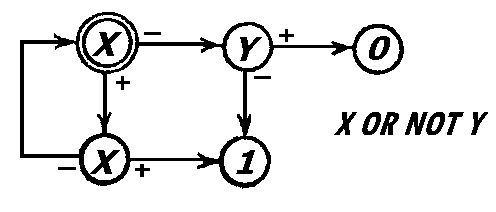
Рис. 14. Логический фрагмент (а) и эквивалентная формула (б)

Тотальный логический фрагмент и логическая формула эквивалентны, если они задают одну и ту же функцию. На рис. 14 приведен пример тотального логического фрагмента и эквивалентной ему логической формулы.

Понятие простое-выражение мы опишем синтаксически, используя следующую грамматику:

простое-выражение ::= {терм | терм{ + | -} простое-выражение}

терм ::={множитель | множитель*терм}

множитель ::={целое-без-знака | идентификатор | (простое-выражение)}

целое-без-знака ::={ цифра | цифра целое-без-знака}

идентификатор ::= буква символ-пробела

Примеры простых выражений:

$1,\ A,\ X+2*X,\ X*D-Y,\ (X+E)*M-2.$

Построение (размеченного двоичного) дерева простого выражения можно описать следующим образом:

1) Дерево простого выражения $\alpha$ есть дерево терма $\alpha$ , если $\alpha$ -- терм; если же $\alpha = \beta\sigma \gamma$ , где $\sigma$ -- это "+" или "-", $\beta$ -- терм, а $\gamma$ -- простое выражение, то корнем дерева $\alpha$ будет вершина, помеченная символом $\sigma$ , ее левым преемником -- корень дерева терма $\beta$ , а правым преемником -- корень дерева простого выражения $\gamma$ .

2) Дерево терма $\alpha$ есть дерево множителя $\alpha$ , если $\alpha$ -- множитель; если же $\alpha = \beta\sigma \gamma$ , где $\sigma$ -- символ операции '*', $\beta$ -- множитель, а $\gamma$ -- терм, то корнем дерева $\alpha$ будет вершина, помеченная операцией $\sigma$ , ее левым преемником -- корень дерева множителя $\beta$ , а правым преемником -- корень дерева терма $\gamma$ .

3) Дерево множителя $\alpha$ есть дерево простого выражения $\beta$ , если $\alpha = (\beta)$ ; если же $\alpha$ -- идентификатор или целое без знака, то его дерево состоит из единственной вершины, помеченной $\alpha$ , без преемников.

На рис. 15 изображены два простых выражения и их деревья.

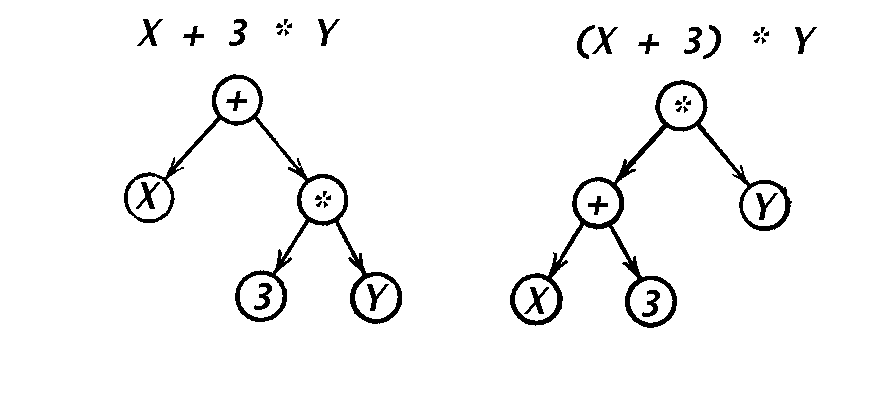
Рис. 15. Два простых выражения и их деревья

Прямая польская запись простого выражения получается последовательным выписыванием пометок вершин во время их посещения при прямом обходе дерева этого выражения.

Обратная польская запись простого выражения получается последовательным выписыванием пометок вершин во время их посещения при обратном обходе дерева этого выражения. При выписывании пометки, когда она является целым без знака, после нее записывается один пробел (это относится как к прямой, так и к обратной польской записи).

Вот несколько примеров прямой и обратной польской записи простых выражений:

Для описания понятия линейная программа мы используем следующую грамматику:

линейная-программа::={присваивание | присваивание; линейная-программа}

присваивание ::= левая-часть:=правая-часть

левая-часть ::= переменная

правая-часть::={ переменная | переменная знак-операции переменная}

переменная::=буква символ-пробела

знак-операции::={ $+ \mid - \mid *$ }

Понятие выполнения линейной программы для заданных начальных значений входящих в нее переменных (все переменные -- целого типа!) совпадает с понятием выполнения последовательности операторов присваивания в Паскале с единственным отличием, что ошибка "переполнение" возникает, если результат операции по модулю превосходит .

Например, если до выполнения линейной программы имеем, то после ее выполнения ; если же до выполнения этой линейной программы , то при ее выполнении возникает ошибка "переполнение".

Для описания понятия простая-программа используем следующую грамматику:

простая-программа ::= заголовок; описания;

заголовок ::= PROGRAM пробел переменная

описания ::= VAR пробел переменная {, переменная}* : INTEGER

составной-оператор ::= BEGIN пробел оператор {; оператор}* END пробел

переменная ::= буква пробел

оператор ::= { READ пробел (переменная) | WRITE пробел (переменная) | составной-оператор |
переменная ::= операнд знак-операции операнд | переменная ::= операнд | IF пробел отношение THEN пробел оператор}

пробел :: = символ-пробела

отношение ::= операнд знак-отношения операнд

операнд ::= { переменная | константа}

знак-операции ::= { $+ \vert - \vert *$ }

знак-отношения ::= {= $< \vert > \vert < \vert > = \vert < >$ }

Простая программа называется правдоподобной, если выполнены следующие условия:

а) каждая из переменных, встречающихся в последовательности операторов тела программы, описана, т.е. встречается и в описаниях программы, причем ровно один раз;

б) в программе нет больше ни одной переменной, совпадающей с названием программы;

в) каждому использованию переменной текстуально предшествует хотя бы один оператор присваивания этой переменной или оператор ввода для этой переменной.

Поскольку определенные выше правдоподобные простые программы являются также и программами языка Паскаль, для них определено понятие выполнение-программы. Отметим, что если простая программа правдоподобна, то при ее выполнении может возникнуть только ошибка "переполнение". В отличие от Паскаля, переполнение возникает при получении результата операции, по модулю превосходящего .

П р и м е р. В результате выполнения правдоподобной простой программы

PROGRAM Z ; VAR X , Y :INTEGER;
BEGIN X:=1 ; Y:=2 ; IF X Y THEN X :=Y ; WRITE ( X );WRITE( Y ) END.

должно быть дважды напечатано число 2.
Для описания понятия полином используем грамматику

полином ::= {0 | одночлен | одночлен { + | - } полином }

одночлен ::= {1 | коэффициент | коэффициент произведение}

произведение ::= { множитель | множитель произведение }

множитель ::= {переменная | переменная показатель}

переменная ::= буква пробел

коэффициент ::= { префикс $\vert$ префикс целое-без-знака}
целое-без-знака ::= { цифра $\vert$ цифра целое-без-знака}
префикс ::={ больше-1| цифра}

больше-0 ::= {1 | больше-1}

больше $больше-1 ::= \{ 2 \vert 3 \vert 4 \vert 5 \vert 6 \vert 7 \vert 8 \vert 9 \}$

цифра ::= {0 | больше-0}

показатель ::= {больше-1 | 1 цифра}

Например, $0,\ 1,\ X\ +2,\ X\ Y\ , X\ -2\ X\ \uparrow 19$ являются полиномами, а $X\ +0,\ 1X,\ X\ \uparrow 20$ -- нет.

Полином называется приведенным, если в каждом его одночлене одна из переменных не встречается более одного раза и нет подобных одночленов.

Например, полиномы $X\ \uparrow 2,\ X\ +X\ Y$ и $X\ -1$ -- приведенные, а $X\ X,\ X\ +3\ X$ и $X\ +2\ -4$ -- нет.

Для описания понятия формулировка-задачи мы снова используем грамматику:

формулировка-задачи ::= список-определений вопрос

список-определений ::= { пробел | список-определений определение}

определение ::= левая-часть IS правая-часть точка

точка ::= .

левая-часть ::= слово

слово ::= { буква | буква слово} пробел

правая-часть ::= предложение

предложение ::={ предложение слово | пробел}

вопрос::= WHAT пробел IS пробел слово?

Текст, построенный в соответствии с определением понятия формулировка задачи, называется корректной формулировкой задачи, если выполнены следующие условия:

а) все слова, встречающиеся в формулировке задачи, отличны от WHAT и IS;

б) все левые части определений в формулировке задачи -- попарно различные слова;

в) в списке определений, следующих после всякого определения $\alpha$ IS $\beta \ .$ , не встречается определений слов из предложения $\beta$ .

Например,

GUTER IS ХОРОШИЙ . IST IS . KNABE IS МАЛЬЧИК . EIN IS . ANDREAS IS АНДРЕЙ . ПЕРЕВОД IS ANDREAS IST EIN GUTER KNABE .WHAT IS ПЕРЕВОД ?

корректная формулировка задачи, а

IS IS IS .WHAT IS IS ? -- нет.

Ответ на конкретную формулировку задачи $\alpha$ WHAT IS $\beta ?$ со списком определений $\alpha$ и словом $\beta$ -- это определение $\beta$ IS $\tau.$ , где предложение $\tau =\phi (\alpha, \beta)$ строится с помощью рекурсивной определяемой функции $\phi$ :

Например, ответ на приведенную выше корректную формулировку задачи имеет вид

ПЕРЕВОД IS АНДРЕЙ ХОРОШИЙ МАЛЬЧИК .

Две корректные формулировки задач называются эквивалентными, если ответы на них совпадают. Например,

B IS A .C IS B .WHAT IS C?

C IS A .WHAT IS C?

-- эквивалентные формулировки задач.

Next:2.4 Геометрия
Up:2 Словарь понятий, используемых в заданиях
Previous:2.2 Грамматики, языки и автоматы