5.2.3 Доказательство свойств программ со структурированными типами данных

Наличие у переменных типа массивов большого числа элементов затрудняет рассмотрение массивов как совокупности независимых переменных. Кроме того, индексы переменных массивов могут вычисляться. Поэтому при описании утверждений о программах с массивами обычно используются дополнительные средства -- так называемые кванторы.

Пусть $m$ и $n$ -- два выражения некоторого скалярного типа, удовлетворяющие условию m<=n. Рассмотрим утверждение , где каждое $E_i$ некоторое утверждение. Оно истинно в любом состоянии, в котором истинно по меньшей мере одно из $E_i$. Это утверждение можно выразить с помощью квантора существования $\exists$ (читается: "существует"): $(\exists i : m \leq i < n : E_i)$ Множество значений, удовлетворяющих $m \leq i < n$, называется областью значения квалифицированной переменной $i$. На естественном языке приведенная запись читается следующим образом:

                         существует, по крайней мере, одно $i$
:                                 такое, что
$m \leq i < n$$i$ принадлежит отрезку m..Pred(n)
:                                 и для него справедливо
$E_i$)                            утверждение $Е_i$.

В подобной линейной форме $(\sum i : m\leq i < n :F_i)$
и $(\prod i : m \leq i < n : F_i)$

можно записывать и такие хорошо известные формы квантификации в математике, как сумма$\sum_{i=m}^{n-1} F_i$ и произведение $\prod_{i=m}^{n-1} F_i$ выражений $F_m,\ldots,F_{n-1}$, где $m$ и $n$ -- выражения целого типа.

Еще один важный квантор -- это квантор общности $\forall$ (читается: "для всех"). Утверждение $(\forall i : m \leq i < n: E_i)$ истинно в некотором состоянии, если и только если $E_i$ истинно в этом состоянии для всех $i$ из области $m \leq i < n$. Другими словами, оно эквивалентно
$True \wedge E_m \wedge E_{succ(m)} \wedge \ldots \wedgeE_{pred(n)}$
$\leftrightarrow \neg \neg(True \wedge E_m \wedgeE_{succ(m)} \wedge \ldots \wedge E_{perd(n)})$ (закон отрицания)
$\leftrightarrow \neg (\neg True \vee \neg E_m \wedge\neg E_{succ(m)} \wedge \ldots \wedge \neg E_{pred(n)}$ (закон де Моргана)
$\leftrightarrow \neg (\exists i : m \leq i < n :\neg E_i)$.

Еще один квантор -- это квантор счета $N$ (читается: "количество различных"). Выражение $(N i : m \leq i < n: E_i)$ обозначает количество различных значений $i$ из области $m \leq i < n$, при которых $E_i$ истинно. Это значит, что
$(\exists i : m \leq i < n :E_i)\leftrightarrow ((N i : m \leq i < n : E_i) \geq 1),$
$(\forall i : m \leq i < n:E_i)\leftrightarrow ((N i:m\leq i< n:E_i)= n - m)$.

До сих пор мы рассматривали области кванторов в виде $m \leq i < n$, где $m$ и $n$ -- выражения некоторого скалярного типа. Утверждения с кванторами по прилегающим друг к другу областям такого вида можно соединить следующим образом:
$(( \exists i : m \leq i < n : E_i)\bigvee (\exists i : n \leq i < k :E_i)) \leftrightarrow (\exists i : m \leq i < k : E_i),$$((\forall i : m \leq i < n : E_i)\bigwedge (\forall i : n \leq i < k : E_i))\leftrightarrow (\forall i : m \leq i < k : E_i),$$((N i : m \leq i < n: E_i) + (N i : n \leq i < k : E_i)) =(N i : m \leq i < k : E_i)$.

Можно обобщить понятие квантора, разрешив квалификацию по другим областям, в том числе и по бесконечным, например:

$(\exists i: R: E)$ и $(\forall i: R: E)$,

где $i$ -- идентификатор, а $R$ и $E$ -- утверждения, которые обычно (но вовсе не обязательно!) содержат $i$. Смысл этих утверждений выражают следующие фразы: "существует значение $i$ из области $R$ (т.е. такое, для которого утверждение $R$ истинно), при котором E истинно"; "для всех значений $i$ из области $R$ утверждение E истинно".

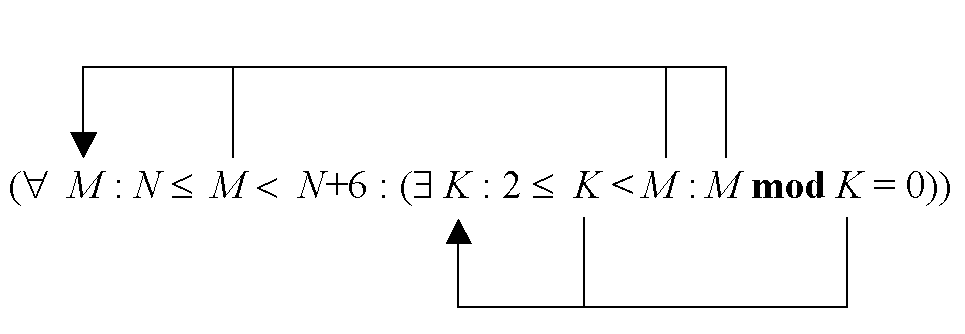
Рассмотрим пример утверждения

$((N I: 1 < I < K: M {\bf mod} I = 0) =0)\wedge (M {\bf mod} K = 0)$

о том, что K-- первое по величине натуральное число, являющееся нетривиальным делителем числа M. Это утверждение истинно, если ни одно из чисел 2,3,...,K-1 не является делителем числа M, а K делит M нацело. Таким образом, истинность утверждения в некотором состоянии выполнения программы зависит от значений переменных M и K, но не от значения $I$; на самом деле переменной с именем $I$ может даже не существовать при данном состоянии вычисления. Ясно, что смысл приведенного утверждения не изменится, если в нем все вхождения $I$ заменить на $L$ следующим образом:

$((N L: 1 < L < K: M {\bf mod} L = O) = O)\wedge (M {\bf mod} K = 0)$.

Очевидно, что в рассмотренном утверждении у идентификатора $I$ иная роль, чем у идентификаторов M и K. Говорят, что M и K свободны в данном утверждении, а идентификатор $I$связан в нем квантором $N$. В приведенном на рис. 5.8 примере все связанные вхождения идентификаторов обозначены стрелками, ведущими от них к кванторам, которыми они связаны (не отмеченные стрелками вхождения являются свободными). Таким образом, каждое утверждение

$(\forall I : R: E)$

вводит новый уровень обозначений. Внутри утверждения можно ссылаться на все имеющиеся вне его переменные, кроме переменной с именем $I$. Эти переменные являются глобальными по отношению к утверждению. Часть $\forall I$ является "описанием" нового локального идентификатора $I$. Имя локального идентификатора не существенно и может быть изменено (всюду в утверждении) без изменения его смысла.

Рис. 5.8: Утверждение с кванторами

В качестве примера использования кванторов рассмотрим задачу сортировки 100 целых чисел -- в порядке неубывания их значений. Ее можно специфицировать следующим образом:

Программа: Сортировка

Вход: $а_1а_2 \ldots а_{100}$
где$(\forall i: 1 \leq i \leq 100: a_i \in Integer)$
Выход: $b_1b_2 \ldots b_{100}$
гдe$(\forall i : 1 \leq i< 100: b_i \leq b_{i+1})$,
$(\forall a: a \in Integer:$$(N i: 1 \leq i \leq 100:a =a_i) = (N i : 1 \leq i < 100: a = b_i))$

Следующая программа является одним из ее возможных решений:

module СОРТИРОВКА;
    (*Сортировка простым выбором*)
    const N = 100;
    type НОМЕР = integer; ВЕКТОР = array N of integer;
    var A : ВЕКТОР ; I,J,K : НОМЕР ; X : integer;
begin
     for I := 1 to N do read(A[I]) end;
     for I := 1 to N-1 do
                    (*{ $(\forall L: 1 \leq L < I: ( \forall M:L < M \leq N: A[L] \leq A[M]))$ }*)
                    K := I; X := A[I];
                    for J := I+1 to N do if A[J] $<$ X then K :=J; X := A[J] end end;
                    (*{$(\forall L: 1 \leq L < I: (\forall M: L < M\leq N: A[L] \leq A[M])), X = A[K],$
                    $I \leq K \leq N, (\forall L: I\leq L \leq N: X \leq A[L])$ }*)
                    A[K] := A[I]; A[I] := X
                    (*{$(\forall L: 1 \leq L \leq I: ( \forall M:L < M \leq N: A[L] \leq A[M]))$}*)
            end;
      (*{$(\forall L: 1 \leq L < N: (\forall M: L < M \leq N:A[L] \leq A[M]))$}*)
      for I := 1 to N do write(A[I]) end
end СОРТИРОВКА.