nextupprevious
 

Next:1.1.2 Что такое компьютер?
Up:1.1 Алгоритмы и функции
Previous:1.1 Алгоритмы и функции

1.1.1 Что такое алгоритм?

Алгоритм -- одно из основных математических понятий. Однако с алгоритмами человеку приходится иметь дело не только в математике. Почти во всех сферах жизни мы повседневно сталкиваемся с инструкциями, предписаниями, рецептами, правилами, в соответствии с которыми происходит та или иная человеческая деятельность. Вот два простых примера.

(А)
1. Опустить жетон в щель телефонного автомата, снять трубку.
2. Услышав длинный гудок, набрать номер 22 44 45.
3. Если раздаются короткие гудки, то повесить трубку, взять жетон и повторить все заново.

(Б)
Растворить 1-2 чайные ложки порошка в горячей воде. Сахар и молоко добавлять по вкусу.

Похожим образом звучат руководства по эксплуатации стиральной и швейной машины, автомобиля, инструкции по конструированию моделей корабля или самолета.

Неформально алгоритм можно определить как точное и понятное, т.е. сформулированное на определенном языке, конечное описание общего способа решения некоторого класса задач с использованием элементарных исполнимых шагов.

Приведенная формулировка скорее поясняет, что такое алгоритм, чем дает точное определение, поскольку она использует весьма неоднозначные термины. Например, что значит "точное" описание? Для кого оно должно быть "понятным"?

Обычно требуют, чтобы алгоритм

-- представлял собой общий метод решения однотипных задач для любых исходных данных -- параметров алгоритма;

-- был составлен настолько точно, чтобы было возможным его однозначное понимание;

-- представлял собой конечное описание, иначе его передача исполнителю длилась бы бесконечно долго.

Кроме того, необходимо каким-то образом задать исполнителя, который вполне самостоятельно, без нашего участия, умел бы исполнять элементарные шаги некоторого фиксированного заранее набора, а также выстраивать друг за другом исполнение этих шагов в том порядке, как это предписано алгоритмом.

Приведенные выше примеры (А) и (Б) не вполне удовлетворяют всем требованиям, предъявляемым к алгоритму: во-первых, здесь нельзя говорить об общем методе, а кроме того, нет и достаточной точности.

От алгоритма требуют часто, чтобы он заканчивался , т.е. выполнял конечное число элементарных шагов при любых исходных данных. Такой алгоритм называют завершающимся. Хотя существуют и незавершающиеся алгоритмы, которые заканчиваются лишь при входных данных из некоторого непустого подмножества, называемого областью применимости алгоритма, мы почти всегда будем рассматривать только завершающиеся алгоритмы.

Простейшими алгоритмами являются известные правила, по которым выполняются арифметические действия в десятичной системе счисления. Например, для суммирования двух многозначных чисел исполнитель рассматривает слагаемые как строки цифр, расположенных "столбиком", и конструирует строку цифр результата справа налево при обработке пар соответствующих цифр слагаемых выполнением операций следующих двух типов: запись соответствующей цифры суммы, пометка о переносе над соседней слева цифрой. Эти операции рассматриваются как элементарные и выполняются исполнителем по раз и навсегда заданной таблице сложения цифр, которую мы в детстве заучиваем наизусть.

В качестве более сложного примера рассмотрим алгоритм Эвклида, решающий все задачи следующего типа: для данных двух натуральных чисел $A$ и $B$ найти их наибольший общий делитель. Очевидно, различных задач такого типа существует столько, сколько есть различных пар натуральных чисел $A$ и $B$. Предписание, пригодное для решения студентом любой из этих задач, можно было бы задать в виде следующей последовательности указаний.

(B)

У к а з а н и е  1. Сотрите все с классной доски, возьмите мел и разделите ее линией на две равные части. В первой части запишите заданное число $A$, а во второй -- заданное число $B$. Переходите к следующему указанию.

У к а з а н и е  2. Сравните два числа, записанных на доске. Если они равны, то прекратите процесс вычисления, взяв в качестве искомого результата первое число. Если нет, переходите к следующему указанию.

У к а з а н и е  3. Посмотрите, не является ли число из первой части доски меньше числа из второй части. Если да, то переставьте числа местами. Переходите к следующему указанию.

У к а з а н и е  4. Вычтите число, находящееся во второй части доски, из числа, находящегося в первой части доски, и запишите остаток в первой части доски вместо числа, находившегося там до вычитания. Переходите к указанию 2.

Итак, следуя данному предписанию, студенту, после того как все 4 указания выполнены, надо возвратиться ко второму, потом к третьему, четвертому и опять ко второму, третьему и т.д., пока не получатся равные числа, т.е. пока не окажется справедливым условие, содержащееся в третьем указании; тогда процесс прекращается. Имея этот алгоритм, нахождение наибольшего общего делителя может осуществить человек, не имеющий ни малейшего представления о сущности самой задачи. Требуется лишь, чтобы этот человек владел русским языком и был способен выполнять те элементарные операции (сравнение двух чисел, вычитание двух чисел, перестановка двух чисел местами и т.п.), из которых складывается процесс решения соответствующих задач, и, кроме того, чтобы он добросовестно и аккуратно руководствовался предложенным предписанием (алгоритмом).

В следующем примере исполнитель "умеет" считать, позиционировать мел на доске и чертить отрезки прямых заданной длины. Алгоритм черчения "улитки" внутри квадрата со стороной $2n$ выглядит следующим образом:

(Г)

Начало алгоритма Спираль ($n$).
Пусть счетчик = 1.
Установить мел на середину квадрата.
Пока счетчик $<2n$, повторять:
[Чертить вверх на 1.
Чертить вправо на счетчик.
Увеличить счетчик на 1.
Чертить вниз на счетчик.
Чертить влево на счетчик.
Чертить вверх на счетчик.
Увеличить счетчик на 1 ]
Конец алгоритма Спираль.

Применение такого алгоритма для $n = 1$ и $n = 2$ построит картинки рис.1.1.

Figure 1.1: Результат работы алгоритма спираль
В следующем примере исполнитель "умеет" выполнять элементарные операции обработки слов.

Пусть $\Sigma$ обозначает некоторый алфавит -- произвольное непустое конечное множество. Элементы алфавита будем называть буквами (или символами). Слово (строка или цепочка) в алфавите $\Sigma$ -- это произвольная последовательность символов из $\Sigma$, расположенных непосредственно друг за другом. Например, 00111 слово в двоичном алфавите { 0,1}. Длина$\mid$$\alpha$$\mid$ cлова $\alpha$ -- это количество символов в нем. Слово длины нуль называется пустым словом и обозначается $\Lambda$. Через$\Sigma^\ast$ oбозначают множество всех слов в алфавите $\Sigma$, включая пустое слово, а $\Sigma^+ = \Sigma^\ast \backslash \{ \Lambda \}$.

Для слов $\alpha,\beta \in \Sigma^\ast$ определена операция конкатенации (или сцепления) $\parallel$, которая дает слово $\alpha \parallel\beta = \alpha \beta$, получающееся последовательным соединением этих слов. Еще две операции предназначены для декомпозиции (разложения) слова на составные части. Если $\alpha =a\beta$, где $a\in \Sigma,$$\alpha,\beta \in \Sigma^\ast$, то Голова$(\alpha) = a$ и Хвост$(\alpha)=\beta$. Например, Голова(00111) = 0 и Хвост(00111) = 0111. Для пустого слова операции Голова и Хвост не определены.

Если исполнитель умеет выполнять перечисленные выше элементарные операции над словами, то мы можем сформулировать для него следующий алгоритм обращения слова:

(Д)

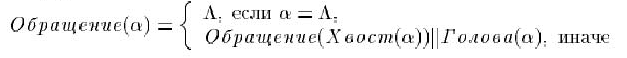
Этот алгоритм можно читать так:

Обращение пустого слова -- это само пустое слово.

Обращение непустого слова получается последовательным соединением обращения хвоста этого слова и его первого символа (головы).

Как будет действовать исполнитель при применении алгоритма обращения к слову 011? В точном соответствии с алгоритмом, пытаясь

а) прежде всего выполнить элементарные операции над словами, являющимися аргументами;

б) использовать определение функции обращение (т.е. собственно алгоритм), если нельзя выполнить ни одну из элементарных операций из-за неподготовленности аргументов. Вычислим значение Обращение(011):

Обращение(011) = Обращение(11) $\parallel$ 0 = (Обращение(1) $\parallel 1) \parallel 0$ = ((Обращение$(\Lambda) \parallel 1) \parallel 1) \parallel 0$ = $((\Lambda \parallel 1) \parallel 1) \parallel 0$ = $(1 \parallel 1) \parallel 0 = 110.$

Для еще одного примера алгоритма предположим, что исполнитель умеет выполнять любые арифметические операции над вещественными числами, а также так называемый оператор присваивания $x := t$, где $x$ -- обозначение некоторой переменной, а $t$ -- произвольное выражение. Исполнение этого присваивания состоит в том, что, во-первых, вычисляется значение выражения $t$ и, во-вторых, полученный результат объявляется новым значением переменной с обозначением $x$. Термин "переменная", который используется здесь для объекта с обозначением $x$ оправдан именно тем, что оператор присваивания может изменять его значение. Если памятью алгоритма назвать множество всех используемых в нем переменных, то возможность изменения их значений приводит нас к понятию состояния памяти и к фон-неймановскому пониманию исполнения алгоритма как процесса изменения состояний памяти.

Задача, на решение которой направлен последний пример алгоритма -- это вычисление значения

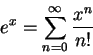
\begin{displaymath}e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \end{displaymath}





для заданного вещественного числа $x$. Это будет пример алгоритма, который не завершается.

(Е)
Начало алгоритма Экспонента (x);
Сумма:= 1;
Слагаемое:= 1;
n := 1;
Повтор: Слагаемое := Слагаемое$ * x/n;$
Сумма : = Сумма + Слагаемое; n : = n + 1;
Иди на Повтор;
Конец алгоритма Экспонента.

Next:1.1.2 Что такое компьютер?
Up:1.1 Алгоритмы и функции
Previous:1.1 Алгоритмы и функции


© В.Н. Касьянов, Е.В.Касьянова, 2004